LL 7 - Find the starting point in Linked List Cycle
 Chetan Datta
Chetan DattaTable of contents

Problem
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, returnnull.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note thatposis not passed as a parameter.
Do not modify the linked list. (link)
Example 1:
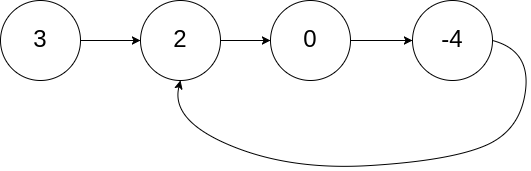
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
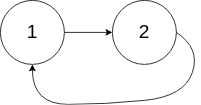
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.
Solution
Brute force Approach
We iterate over the nodes of the linked list one by one and place each node into a set. We use a set because it allows us to check whether we have encountered a particular node before. If we encounter a node that is already in the set, it indicates that we are in a loop. In such a case, we return the node as it is the starting point of the loop.
public class Solution {
public ListNode detectCycle(ListNode head) {
Set<ListNode> set = new HashSet<>();
ListNode temp = head;
while(temp!=null && !set.contains(temp)){
set.add(temp);
temp = temp.next;
}
return temp;
}
}
Optimal Approach
Step 1: Detect Loop
First step is to detect the loop using slow and fast pointers (link)
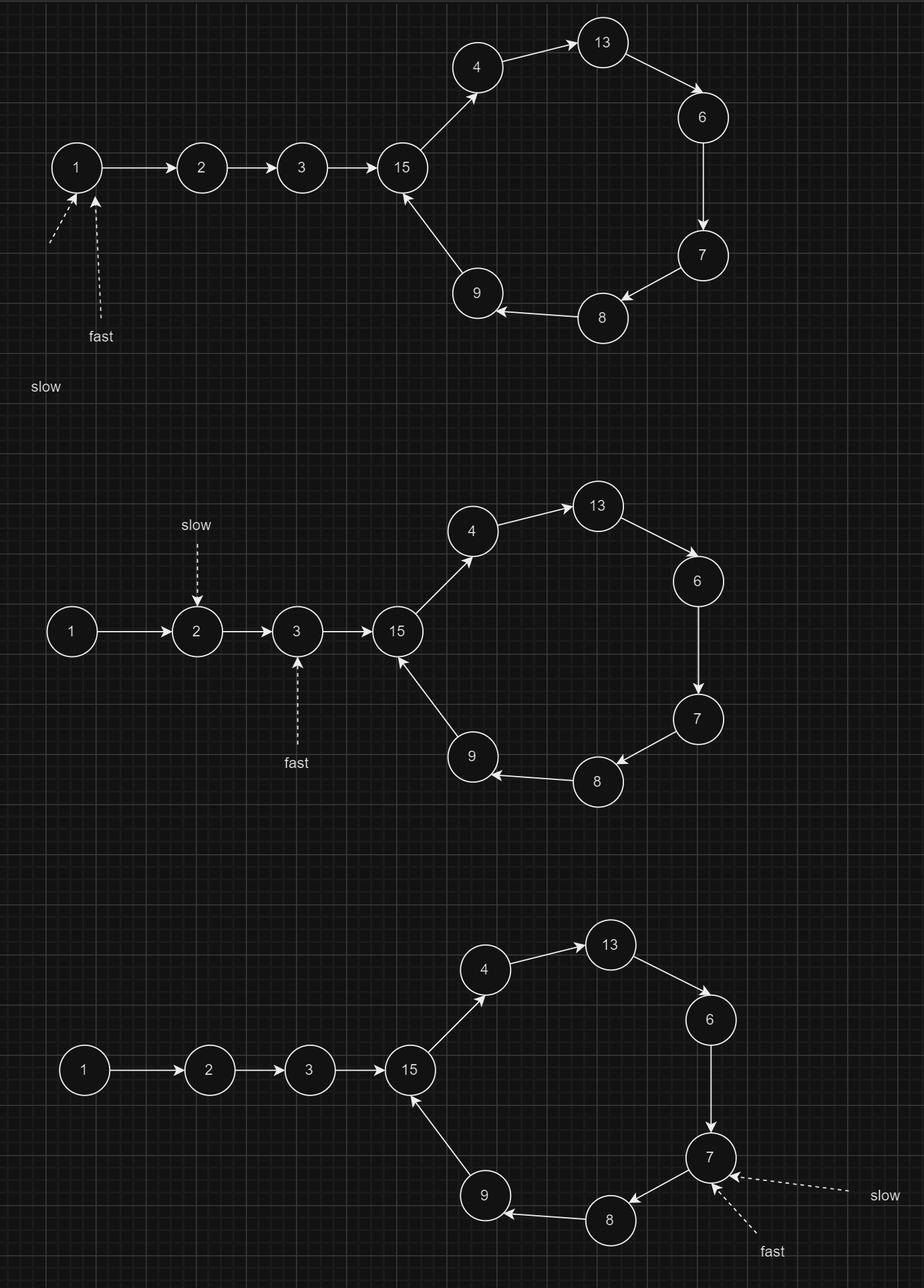
Step 2: Place Slow pointer at head
Place the slow pointer at the head position.
Now move slow and fast pointer one step each at a time.
At the end they collide at the starting point of the loop.
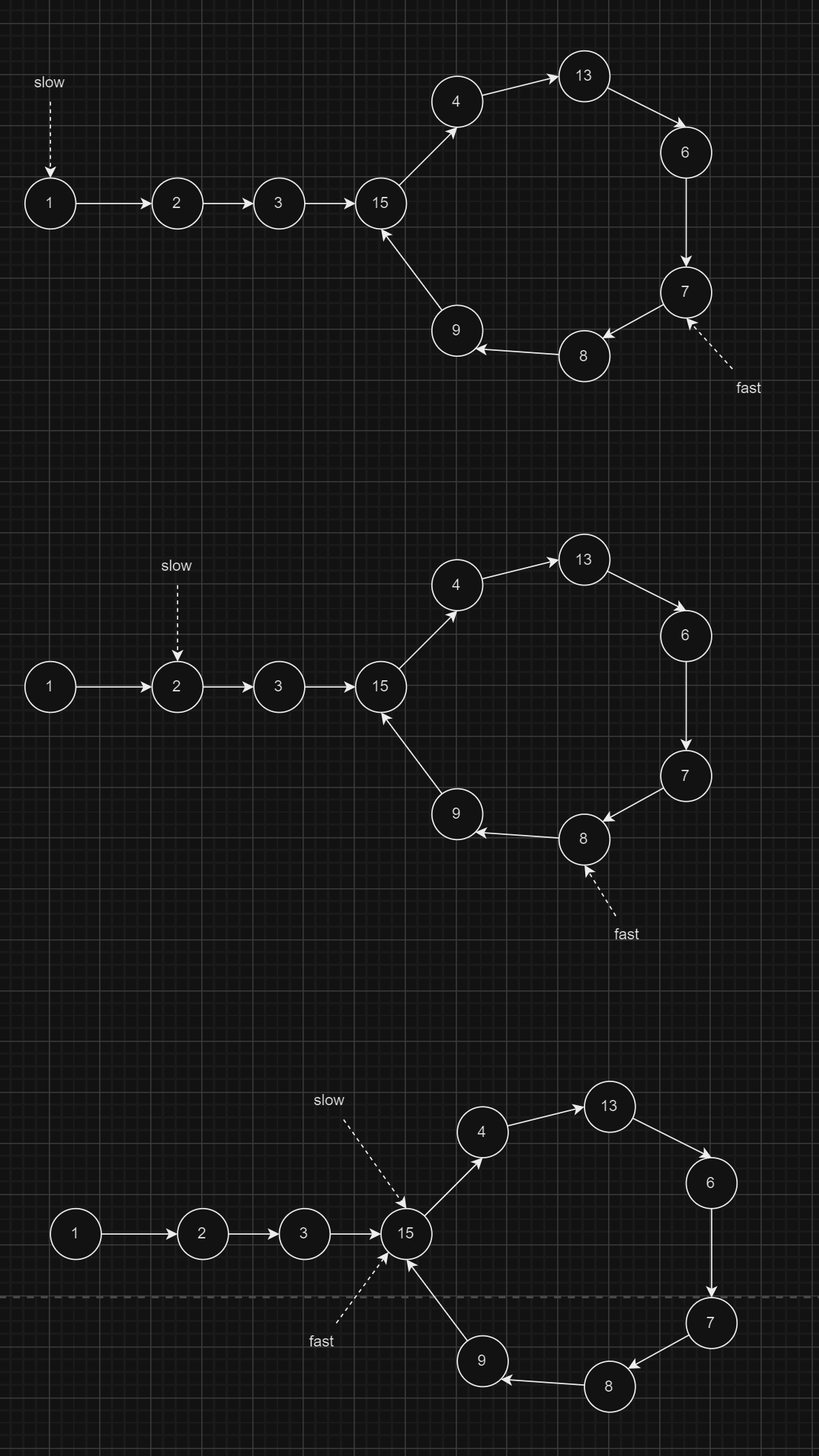
Explanation for placing the slow pointer at the head:
Assume that the distance from the head to the starting point of the loop is L1.
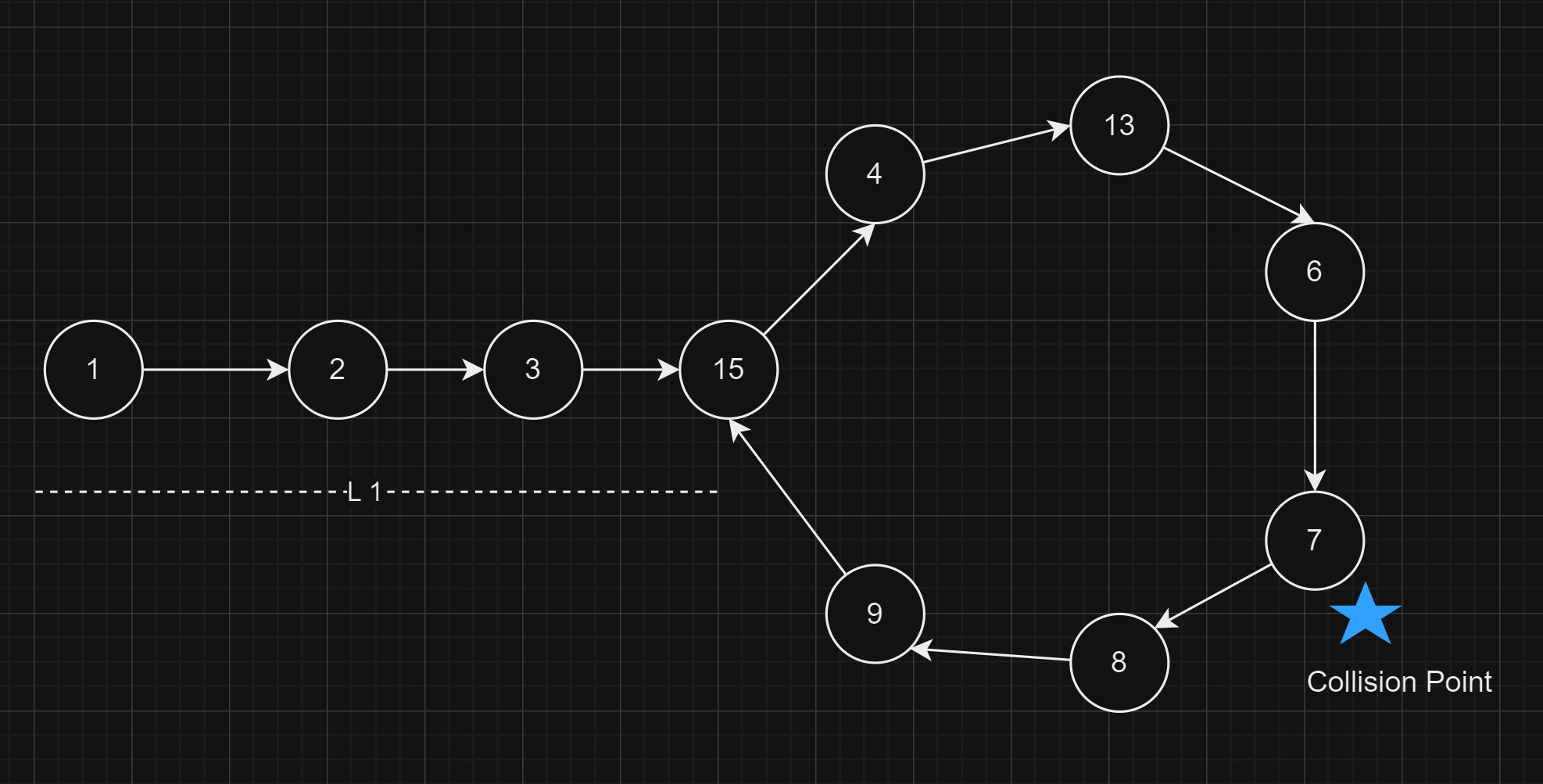
Now, we have to prove that the distance from the point of collision of the slow and fast pointers to the starting point of the loop is also L1.
Proof:
Given that the distance between the head and the starting point of the loop is L1.
Now, move the slow and fast pointers from the head. Get the slow pointer to the starting point of the loop.
This means the slow pointer travelled a distance of
L1and the fast pointer travelled a distance of2*L1. The fast pointer isL1distance ahead of slow pointer.Also the fast pointer travelled L1 distance on the loop.
Assume that the distance between the fast and slow pointers in the forward direction is d.
That means length of the loop is L1 + d.
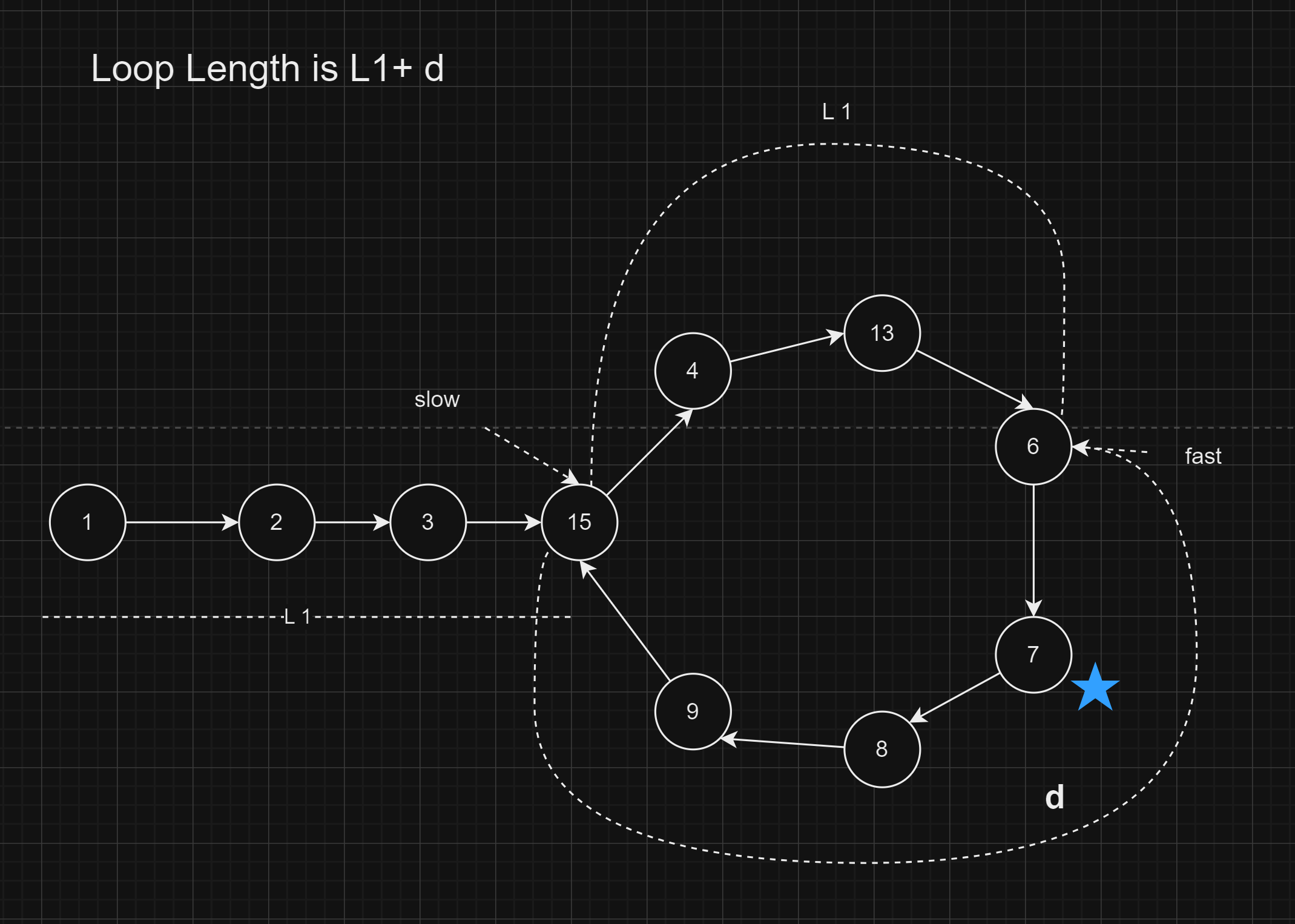
If the fast pointer wants to collide with the slow pointer, then it has to travel
2*ddistance.This means the slow pointer travelled a distance d from the starting point of the loop.
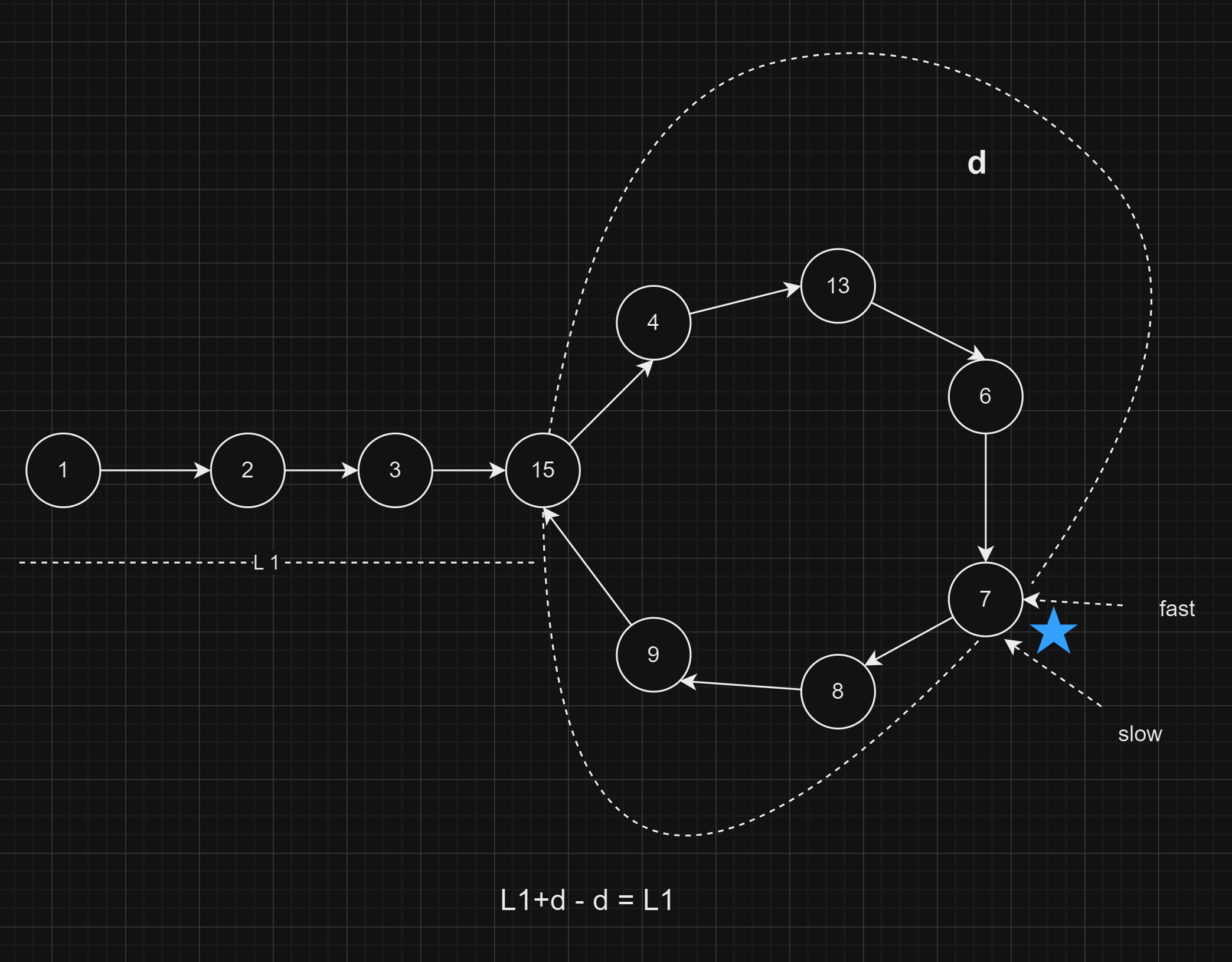
This means the slow pointer covered
ddistance on the loop when it collided.From the collision point to the starting point, the distance left is length of loop minus the
ddistance.The length of the loop is
L1 + d. Hence, the distance from the collision point to the starting point isL1+ d - d = L1. Which isL1itself.
Code
public class Solution {
public ListNode startingPoint(ListNode head, ListNode fast){
ListNode slow = head;
while(slow!=fast){
slow = slow.next;
fast = fast.next;
}
return slow;
}
public ListNode detectCycle(ListNode head) {
if(head==null || head.next ==null) return null;
ListNode slow = head;
ListNode fast = head;
while(fast!=null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow==fast) return startingPoint(head,fast);
}
return null;
}
}
Subscribe to my newsletter
Read articles from Chetan Datta directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Chetan Datta
Chetan Datta
I'm someone deeply engrossed in the world of software developement, and I find joy in sharing my thoughts and insights on various topics. You can explore my exclusive content here, where I meticulously document all things tech-related that spark my curiosity. Stay connected for my latest discoveries and observations.