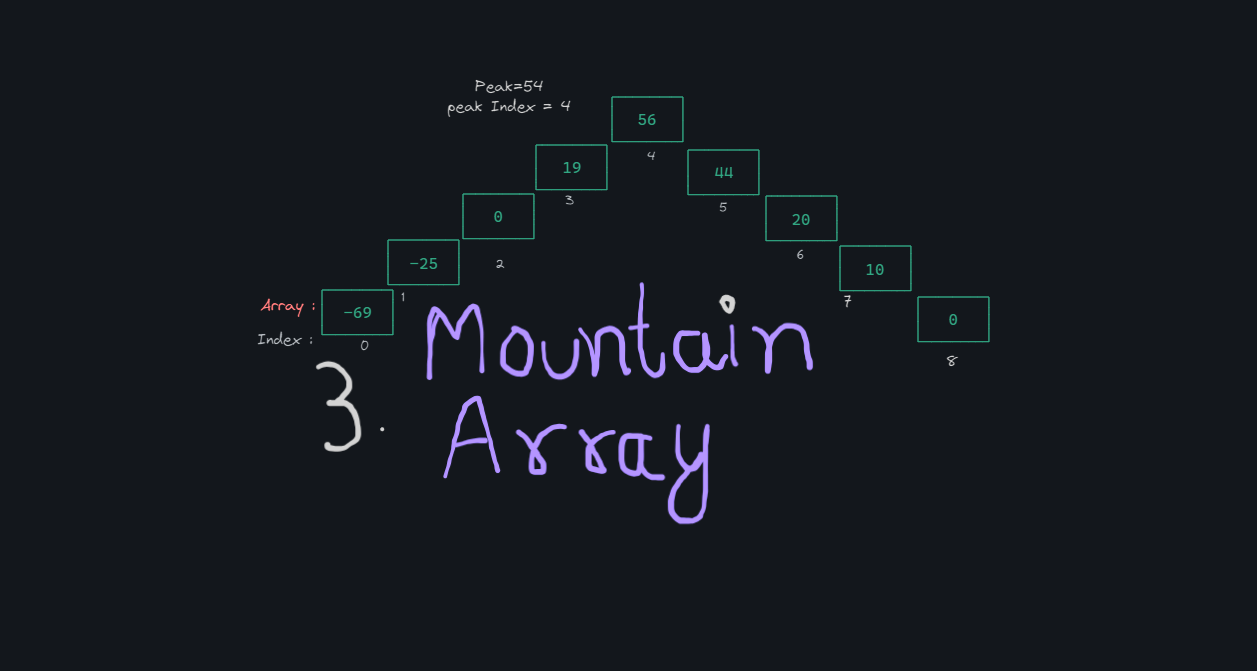
---

What is a Mountain array?

It's an array where the elements first increase in ascending order, reach a peak, and then decrease in descending order.

The number of elements in a mountain array is at least 3.
arr.length>=3

example:

• [1,2,3,4,5,4,3,2,1]

• [4,7,9,12,15,0,-2,-5,-7,-9]

• [4,7,9,12,15,56,66,67,99,-34,-342,-2222]

What is Peak ?

The peak in a mountain array is the highest element in the sequence. It is the point where the elements, which have been increasing in ascending order, reach their maximum value. After this peak element, the array begins to decrease in descending order. To find the peak, you can look for the element that is greater than its neighbors. This element will have all preceding elements in increasing order and all following elements in decreasing order. Identifying this peak is crucial as it defines the transition point in the mountain array.

example:

• [1,2,3,4,5,4,3,2,1]peak=5

• [4,7,9,12,15,0,-2,-5,-7,-9]peak=15

• [4,7,9,12,15,56,66,67,99,-34,-342,-2222]peak=99

How to find Peak?

Code:

// Use this only if u are confirmed that the array u are passing here is 
// an mountain array.
    static int findPeak(int[] arr) {
        int s = 0, e = arr.length - 1, m = 0;
        while (s < e) {
            m = (s + e) / 2;
            if (arr[m] > arr[m + 1]) {
                e = m;
            }
            else {
                s = m + 1;
            }
        }
        return s;
    }

Explanation:

1. Initialization:

   • s (start) is set to 0.

   • e (end) is set to the last index of the array.

   • m (mid) is initialized to 0.

2. While Loop:

   • The loop runs as long as s is less than e.

3. Calculate Mid:

   • m is calculated as the average of s and e.

4. Check Mid Against Next Element:

   • If arr[m] is greater than arr[m + 1], it means the peak is in the left half (including m), so set e to m.

   • Otherwise, the peak is in the right half, so set s to m + 1.

5. End of Loop:

   • When s equals e, the loop ends, and s (or e) is the index of the peak element.

6. Return:

   • Return s, which is the index of the peak element.

How to search in Mountain Array?

Algorithm Overview:

1. First find the peak of the array.

2. Next check if the peal is equal to the target.

3. If not equal, search from the zeroth index to the (peak-1)th index using ascending binary search. If the target is found, return the index.

4. If it is not found in the first part of the array, use descending binary search to find it in the second part of the array and return the index.

5. If the target is still not found, return -1, as it does not exist in the array.

Code:

class Solution {
    public int findInMountainArray(int target, MountainArray arr) {
        int start = 0;
        int end = arr.length() - 1;
        while (start < end) { // s<e because we will get the peak when s==e
            int mid = ((start + end) / 2);
            if (arr.get(mid) > arr.get(mid + 1)) {
                end = mid;
            } else {
                start = mid + 1;
            }
        }
        // now start = end = mid
        int peakIndex = start;
        System.out.println("peak: " + peakIndex);
        if (target == arr.get(peakIndex)) {
            return peakIndex;
        }
        int as = ascendingBinarySearch(end, arr, target);
        int des = descendingBinarySearch(start, arr, target);

        if (as == -1 && des == -1) {
            // System.out.println("Element not found in Mountain array");
            return -1;
        } else if (as == -1) {
            // System.out.println("target at: " + des);
            return des;
        } else if (des == -1) {
            // System.out.println("target at: " + as);
            return as;
        } else {
            // System.out.println("target at: " + as);
            // System.out.println("target at: " + des);
            // Element is found on both sides
            return as; 
        }
    }
      // ascending binary search
    static int ascendingBinarySearch(int end, MountainArray arr, int target) {
        int start = 0;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (target > arr.get(mid)) {
                start = mid + 1;
            } else if (target < arr.get(mid)) {
                end = mid - 1;
            } else {
                return mid;
            }
        }
        return -1;
    }

    // descending binary search
    static int descendingBinarySearch(int start, MountainArray arr, int target) {
        // int start = 0;
        int end = arr.length() - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (target > arr.get(mid)) {
                end = mid - 1;
            } else if (target < arr.get(mid)) {
                start = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

Code Explanation:

Class: Solution

Method:findInMountainArray

1. Find the Peak:

   • Initialize start to 0 and end to the last index of the array.

   • Use a while loop to find the peak element where arr.get(mid) > arr.get(mid + 1).

   • The loop continues until start equals end, giving the peak index.

2. Check Peak for Target:

   • If the peak element is the target, return its index.

3. Search in Ascending and Descending Halves:

   • Use ascendingBinarySearch for the left side of the peak.

   • Use descendingBinarySearch for the right side of the peak.

   • If both searches return -1, the target is not in the array.

   • If only one search finds the target, return that index.

   • If both searches find the target, return the index from the ascending search.

Supporting Methods:

Method:ascendingBinarySearch

• Searches for the target in the ascending part of the array.

• Performs a binary search between start (0) and end (peak index).

• Returns the index if found, otherwise -1.

Method:descendingBinarySearch

• Searches for the target in the descending part of the array.

• Performs a binary search between start (peak index) and end (last index).

• Returns the index if found, otherwise -1.

Detailed Explanation:

1. Finding the Peak:

   • The loop iterates, adjusting start and end to converge on the peak.

   • mid is recalculated each iteration to check if the array value is greater than the next element.

   • The peak is the highest point in the mountain array.

2. Binary Search Methods:

   • ascendingBinarySearch: Traditional binary search, but only up to the peak.

   • descendingBinarySearch: Similar, but in reverse order, adjusting for the descending part of the array.

Summary:

This article explains the concept of a mountain array, which is an array that increases to a peak and then decreases. It details how to find the peak element in such an array using a binary search algorithm and provides a solution for searching for a target element within the mountain array. The methods used include finding the peak, performing binary search on both the ascending and descending parts of the array, and efficiently identifying the target's index or determining its absence.