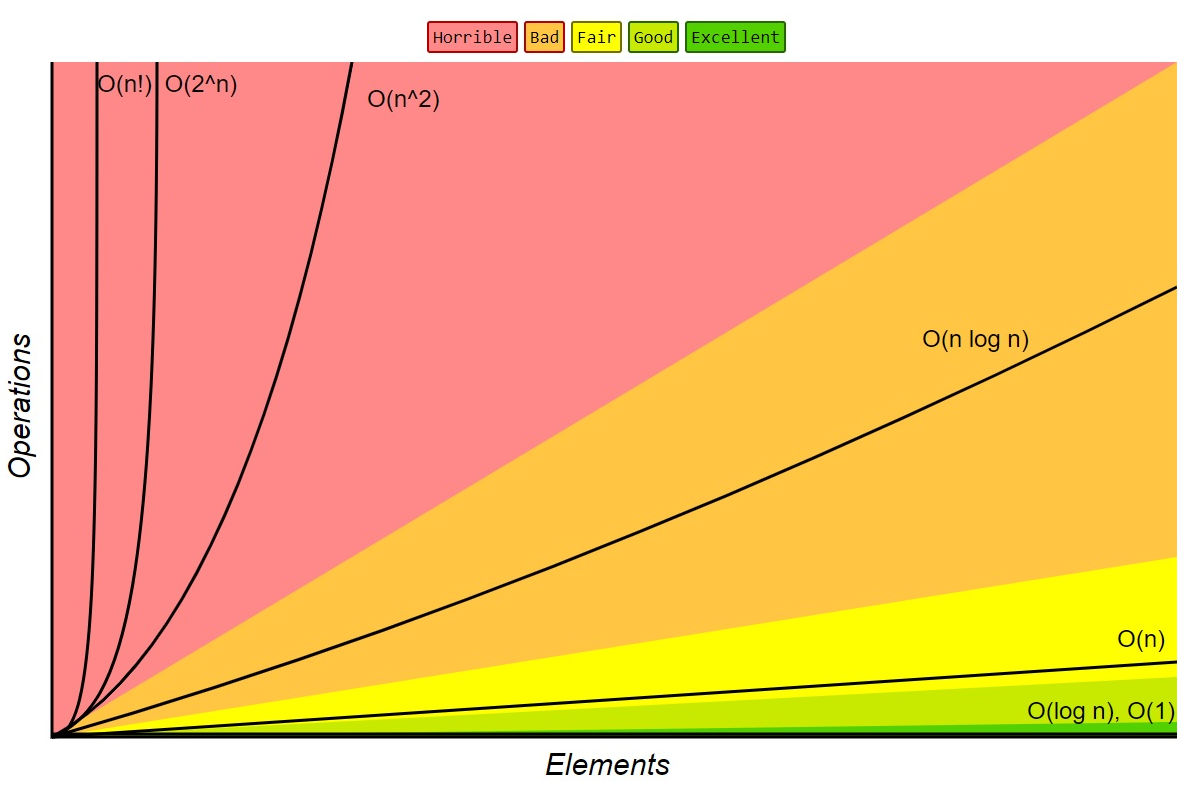
Introduction

Controlling Complexity is the essence of Computer Programming

~ Brian Kernighan

Algorithmic complexity is a measure of how efficiently an algorithm performs given an input of size n. Essentially, it tells us how the algorithm's performance scales as the input grows larger. It is concerned about how fast or slow particular algorithm performs. If an algorithm has to scale, it should compute the result within a finite and practical time bound even for large values of n. For this reason, complexity is calculated asymptotically as n approaches infinity. While complexity is usually in terms of time, sometimes complexity is also analyzed in terms of space, which translates to the algorithm's memory requirements.

Example : -

Imagine a pile of Papers

• Small pile: You can sort it quickly.

• Large pile: Sorting takes longer.

How much longer? That depends on how you sort.

Sorting Methods -

1. Check each paper against all others (like finding the smallest and putting it first, then the next smallest, and so on). This is slow, especially for big piles.

2. Divide the pile in half, sort each half, then combine (like sorting cards). This is usually faster.

How to measure the time it takes

Instead of using fancy math terms, let's say:

• Time grows as fast as the pile size: This is like Method 1. If the pile doubles, the sorting time roughly doubles too.

• Time grows slowly as the pile size grows: This is like Method 2. Even with a huge pile, the sorting time increases gradually.

In simpler terms

• Slow methods: The bigger the job, the much longer it takes.

• Fast methods: The bigger the job, the time increases, but not as dramatically

How to Calculate Algorithmic Complexity ?

There are basically two types of ' Algorithmic Complexities ' .

• Time Complexity : - Time complexity is a way to measure how long an algorithm takes to run as the input size grows. It's expressed in terms of the input size, typically denoted as n.

• Space complexity:- is a measure of the amount of memory space required by an algorithm to solve a problem. It's essentially the algorithm's appetite for memory as the input size grows.

Big - O Notation :-

Big O notation is a mathematical notation used in computer science to**describe the upper bound or worst-case scenario of the runtime complexity of an algorithm in terms of the input size.** It provides a standardized and concise way to express how the performance of an algorithm scales as the size of the input grows.

Key Concepts

• Asymptotic Behavior: Big O focuses on the behavior of the algorithm as the input size grows infinitely large. It ignores constant factors and lower-order terms.

• Upper Bound: Big O provides an upper bound on the growth rate of the algorithm's runtime or space usage.

• Worst-Case Scenario: It represents the maximum amount of time or space an algorithm could potentially take for a given input size.

Mathematical Representation of Big - O Notation : -

O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }

Apart from Big-O Notation there are two other Notations :

1. Theta (Θ) Notation [ Average Case Compexity]

2. Omega Notation (Ω-notation) [ Best Case Complexity]

Common Time Complexities

• O(1): Constant Time

  • The algorithm's runtime is independent of the input size.

  • Examples : Accessing an array element by index, simple arithmetic operations.

• O(log n): Logarithmic Time

  • The runtime grows logarithmically with the input size.

  • Examples : Binary search, finding the greatest common divisor.

• O(n): Linear Time

  • The runtime grows linearly with the input size.

  • Examples: Linear search, finding the maximum element in an array.

• O(n log n): Linearithmic Time

  • The runtime grows slightly faster than linear but slower than quadratic.

  • Examples: Merge sort, quicksort.

• O(n^2): Quadratic Time

  • The runtime grows quadratically with the input size.

  • Examples: Bubble sort, selection sort.

• O(2^n): Exponential Time

  • The runtime grows exponentially with the input size. www.netguru.com

  • Examples: Generating all subsets of a set.

Resources to Understand Complexities in Depth :-

• https://youtube.com/playlist?list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&si=cSJBZcl-7PQtbRPr

Conclusion :-

Algorithmic complexity is the cornerstone of efficient problem-solving in computer science. By understanding and analyzing the time and space requirements of algorithms, we gain invaluable insights into their performance characteristics.

Key Takeaways : -

The Big Three

There are three primary asymptotic notations:

1. Big O notation (O): This represents the upper bound of an algorithm's running time. It tells us the worst-case scenario for how long the algorithm might take.

2. Big Omega notation (Ω): This represents the lower bound of an algorithm's running time. It tells us the best-case scenario.

3. Big Theta notation (Θ): This represents both the upper and lower bounds, meaning the algorithm's running time will always be within a certain range.