Implementación de Sistemas de Inferencia Difusa con Inferfuzzy en Python
 leynierdev
leynierdev
Inferfuzzy es una biblioteca de Python para implementar Sistemas de Inferencia Difusa.
Empezando
Instalación
pip install inferfuzzy
Uso
Creación de Variables Lingüísticas y Conjuntos Difusos
variable_1 = Var("variable_name_1")
variable_1 += "set_name_1", ZMembership(1, 2)
variable_1 += "set_name_2", GaussianMembership(3, 2)
variable_1 += "set_name_3", SMembership(4, 6)
variable_2 = Var("variable_name_2")
variable_2 += "set_name_4", GammaMembership(70, 100)
variable_2 += "set_name_5", LambdaMembership(40, 60, 80)
variable_2 += "set_name_6", LMembership(30, 50)
Declaración de Reglas Semánticas y Método de Inferencia
mamdani = MamdaniSystem(defuzz_func=centroid_defuzzification)
mamdani += variable_1.into("set_name_1") | variable_1.into("set_name_3"), variable_2.into("set_name_5")
mamdani += variable_1.into("set_name_2"), variable_2.into("set_name_4")
Uso del Método de Inferencia Difusa para Valores Ingresados por el Usuario
variable_1_val = float(input())
mamdani_result: float = mamdani.infer(variable_name_1=variable_1_val)["variable_name_2"]
Características del Sistema de Inferencia
La biblioteca incluye implementaciones de los métodos de inferencia Mamdani y Larsen. Sin embargo, se pueden implementar otros métodos de inferencia partiendo de una base común.
Los métodos de inferencia requieren una función de defuzzificación. La biblioteca incluye implementaciones de las siguientes funciones de defuzzificación: Centroide, Bisectriz, Máximo Central, Máximo más Pequeño y Máximo más Grande.
Durante el proceso de definición de los conjuntos difusos, se requiere una función de membresía que puede ser implementada o utilizar una de las disponibles en la biblioteca.
Funciones de membresía implementadas en Inferfuzzy:
Función Gamma
Función Lambda o Triangular
Función Pi o Trapezoidal
Función S
Función Z
Función Gaussiana
La T-conorm y T-norm utilizadas en las reglas de inferencia, así como el método de agregación de los conjuntos, se pueden sobrescribir. Por defecto, son mínimo, máximo y máximo respectivamente.
Es posible definir más de una variable de salida para el sistema de inferencia difusa implementado en la biblioteca.
Estructura de la Implementación
La implementación se basa en siete clases fundamentales:
MembershipBaseSetBaseVarBaseRulePredicateVarSetInferenceSystem
Membership
Clase que representa una función de membresía junto a los puntos (items) internamente.
class Membership:
def __init__(self, function: Callable[[Any], Any], items: list):
self.function = function
self.items = items
def __call__(self, value: Any):
return self.function(value)
BaseSet
Clase que representa un conjunto difuso. Recibe un objeto de tipo Membership representando la función de membresía del conjunto y un método de agregación.
class BaseSet:
def __init__(
self,
name: str,
membership: Membership,
aggregation: Callable[[Any, Any], Any],
):
self.name = name
self.membership = membership
self.aggregation = aggregation
def __add__(self, arg: "BaseSet"):
memb = Membership(
lambda x: self.aggregation(
self.membership(x),
arg.membership(x),
),
self.membership.items + arg.membership.items,
)
return BaseSet(
f"({self.name})_union_({arg.name})",
memb,
aggregation=self.aggregation,
)
BaseVar
Clase que representa una variable lingüística. Recibe una función de unión, una función de intercepción y una lista de objetos de tipo BaseSet representando los conjuntos difusos de la variable.
class BaseVar:
def __init__(
self,
name: str,
union: Callable[[Any, Any], Any],
inter: Callable[[Any, Any], Any],
sets: Optional[List[BaseSet]] = None,
):
self.name = name
self.sets = {set.name: set for set in sets} if sets else {}
self.union = union
self.inter = inter
def into(self, set: Union[BaseSet, str]) -> VarSet:
set_name = set.name if isinstance(set, BaseSet) else set
if set_name not in self.sets:
raise KeyError(f"Set {set_name} not found into var {self.name}")
temp_set = self.sets[set_name]
return VarSet(self, temp_set, self.union, self.inter)
BaseRule
Clase que representa una regla de inferencia. Recibe un objeto de tipo Predicate representando el antecedente de la regla.
class BaseRule:
def __init__(self, antecedent: Predicate):
self.antecedent = antecedent
def __call__(self, values: dict):
raise NotImplementedError()
BaseRule no contiene consecuencias porque las consecuencias de todos los tipos de reglas no son de la misma estructura. La clase Rule hereda de BaseRule y representa las reglas en las que el sistema produce un conjunto o más como resultado.
class Rule(BaseRule):
def __init__(self, antecedent: Predicate, consequences: List[VarSet]):
super(Rule, self).__init__(antecedent)
self.consequences = consequences
def aggregate(self, set: BaseSet, value: Any) -> BaseSet:
raise NotImplementedError()
def __call__(self, values: dict):
value = self.antecedent(values)
return {
consequence.var.name: self.aggregate(
consequence.set,
value,
)
for consequence in self.consequences
}
Predicate
Clase que representa a los antecedentes. De ella heredan cuatro clases: AndPredicate, OrPredicate, NotPredicate y VarSet. Las primeras tres representan las relaciones lógicas de unión, intercepción y negación, y la última representa la inclusión de una variable en un determinado conjunto, siendo esta la clase básica para representar a los antecedentes.
class Predicate:
def __init__(
self,
union: Callable[[Any, Any], Any],
inter: Callable[[Any, Any], Any],
) -> None:
self.union = union
self.inter = inter
def __call__(self, values: dict):
raise NotImplementedError()
def __and__(self, other: "Predicate"):
return AndPredicate(self, other, self.union, self.inter)
def __or__(self, other: "Predicate"):
return OrPredicate(self, other, self.union, self.inter)
def __invert__(self):
return NotPredicate(self, self.union, self.inter)
VarSet
class VarSet(Predicate):
def __init__(
self,
var: "BaseVar",
set: BaseSet,
union: Callable[[Any, Any], Any],
inter: Callable[[Any, Any], Any],
):
super(VarSet, self).__init__(union, inter)
self.var = var
self.set = set
def __call__(self, values: dict):
return self.set.membership(values[self.var.name])
InferenceSystem
Clase que representa el sistema de inferencia. Recibe las reglas y una función de defuzzificación. El método infer permite realizar la inferencia según los valores proveídos.
class InferenceSystem:
def __init__(
self,
rules: Optional[List[BaseRule]] = None,
defuzz_func: Optional[Callable[[BaseSet], Any]] = None,
):
self.rules = rules if rules else []
self.defuzz_func = defuzz_func
def infer(
self,
values: dict,
defuzz_func: Optional[Callable[[BaseSet], Any]] = None,
) -> Dict[str, Any]:
if not self.rules:
raise Exception("Empty rules")
if self.defuzz_func is None and defuzz_func is None:
raise Exception("Defuzzification not found")
func = self.defuzz_func if defuzz_func is None else defuzz_func
set: Dict[str, BaseSet] = self.rules[0](values)
for rule in self.rules[1:]:
temp: Dict[str, BaseSet] = rule(values)
for key in temp:
set[key] += temp[key]
result: Dict[str, Any] = {}
for key in set:
result[key] = func(set[key])
return result
Ejemplo de Uso de Inferfuzzy
Como ejemplo, se utilizará el siguiente problema: se desea inferir el porcentaje de la cantidad de un determinado producto que se ha vendido en un día en un restaurante, cafetería, etc.
Por ejemplo, el producto Pollo, se desea conocer bajo determinadas condiciones qué porcentaje del Pollo sacado del almacén dispuesto para venderse ese día se termina vendiendo.
Para la implementación se seleccionaron 4 variables lingüísticas: 3 de entrada y 1 de salida.
Cantidad de platos o derivados del producto que se vende (
variety):Baja:
low <= 2. Función de Membresía: ZNormal:
1 <= normal <= 5. Función de Membresía: GaussianaAlta:
high >= 4. Función de Membresía: S
Porcentaje de la variable
varietydel total de platos o derivados de productos que se vende (diversity):Baja:
low >= 70. Función de Membresía: GammaNormal:
40 <= normal <= 80. Función de Membresía: LambdaAlta:
high <= 50. Función de Membresía: L
Porcentaje de la utilización del local (
clients):Baja:
low <= 40. Función de Membresía: LNormal:
30 <= normal <= 90. Función de Membresía: LambdaAlta:
high >= 80. Función de Membresía: Gamma
Porcentaje de la cantidad del producto que se vendió en el día (
sales):Baja:
low <= 60. Función de Membresía: LNormal:
30 <= normal <= 90. Función de Membresía: LambdaAlta:
high >= 90. Función de Membresía: Gamma
Declaración de las Variables Lingüísticas y Conjuntos Difusos en Inferfuzzy
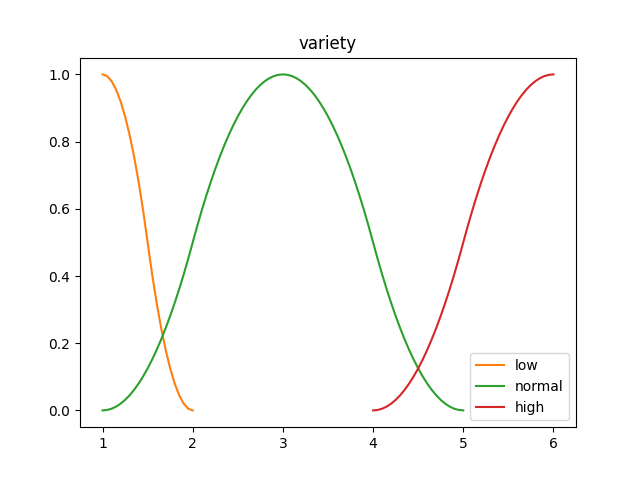
variety_var = Var("variety")
variety_var += "low", ZMembership(1, 2)
variety_var += "normal", GaussianMembership(3, 2)
variety_var += "high", SMembership(4, 6)
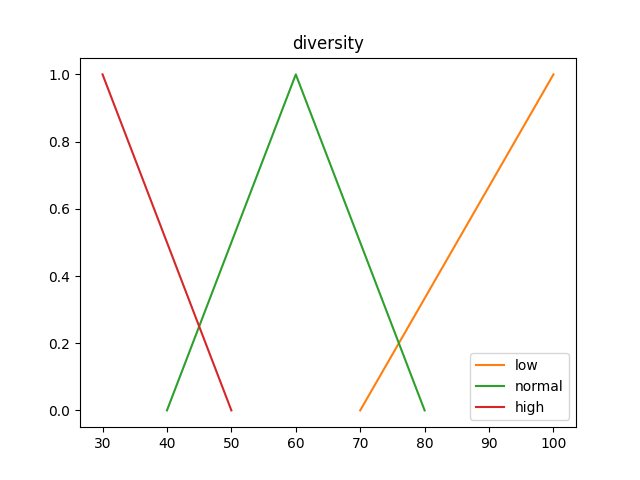
diversity_percent_var = Var("diversity")
diversity_percent_var += "low", GammaMembership(70, 100)
diversity_percent_var += "normal", LambdaMembership(40, 60, 80)
diversity_percent_var += "high", LMembership(30, 50)
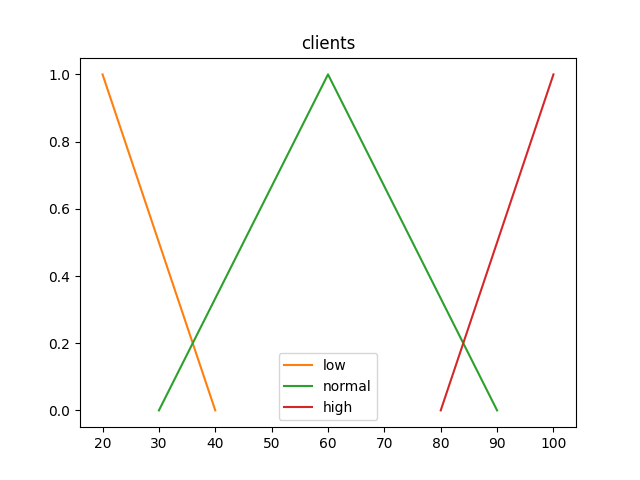
clients_percent_var = Var("clients")
clients_percent_var += "low", LMembership(20, 40)
clients_percent_var += "normal", LambdaMembership(30, 60, 90)
clients_percent_var += "high", GammaMembership(80, 100)
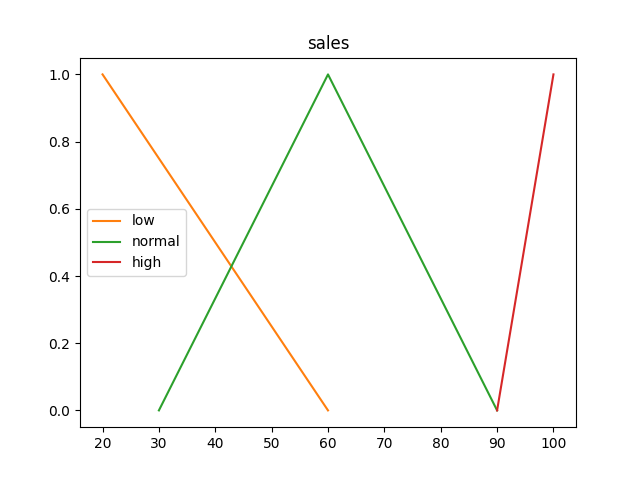
sales_percent_var = Var("sales")
sales_percent_var += "low", LMembership(20, 60)
sales_percent_var += "normal", LambdaMembership(30, 60, 90)
sales_percent_var += "high", GammaMembership(90, 100)
Gráficos de Pertenencia de los Conjuntos por Cada Variable
Reglas de Inferencia
| variety | diversity | clients | sales |
| low | low | low | low |
| low | low | normal | normal |
| low | low | high | high |
| low | normal | low | low |
| low | normal | normal | low |
| low | normal | high | normal |
| low | high | low | low |
| low | high | normal | low |
| low | high | high | normal |
| normal | low | low | low |
| normal | low | normal | normal |
| normal | low | high | high |
| normal | normal | low | low |
| normal | normal | normal | normal |
| normal | normal | high | normal |
| normal | high | low | low |
| normal | high | normal | low |
| normal | high | high | normal |
| high | low | low | low |
| high | low | normal | normal |
| high | low | high | high |
| high | normal | low | low |
| high | normal | normal | low |
| high | normal | high | high |
| high | high | low | low |
| high | high | normal | low |
| high | high | high | normal |
Declaración de las Reglas de Inferencia en Inferfuzzy
mamdani = MamdaniSystem(
defuzz_func=centroid_defuzzification,
)
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("low")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("low")
& clients_percent_var.into("normal")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("low")
& clients_percent_var.into("high")
), sales_percent_var.into("high")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("normal")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("normal")
& clients_percent_var.into("normal")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("normal")
& clients_percent_var.into("high")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("high")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("high")
& clients_percent_var.into("normal")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("low")
& diversity_percent_var.into("high")
& clients_percent_var.into("high")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("low")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("low")
& clients_percent_var.into("normal")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("low")
& clients_percent_var.into("high")
), sales_percent_var.into("high")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("normal")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("normal")
& clients_percent_var.into("normal")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("normal")
& clients_percent_var.into("high")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("high")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("high")
& clients_percent_var.into("normal")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("normal")
& diversity_percent_var.into("high")
& clients_percent_var.into("high")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("low")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("low")
& clients_percent_var.into("normal")
), sales_percent_var.into("normal")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("low")
& clients_percent_var.into("high")
), sales_percent_var.into("high")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("normal")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("normal")
& clients_percent_var.into("normal")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("normal")
& clients_percent_var.into("high")
), sales_percent_var.into("high")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("high")
& clients_percent_var.into("low")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("high")
& clients_percent_var.into("normal")
), sales_percent_var.into("low")
mamdani += (
variety_var.into("high")
& diversity_percent_var.into("high")
& clients_percent_var.into("high")
), sales_percent_var.into("normal")
De manera análoga sería para Larsen utilizando la clase LarsenSystem.
Resultados
Variety Value: 10
Diversity Percent: 50
Clients Percent: 50
Mamdani: 35.11%
Larsen 32.82%
Variety Value: 2
Diversity Percent: 100
Clients Percent: 100
Mamdani: 96.22%
Larsen 100.00%
Variety Value: 4
Diversity Percent: 40
Clients Percent: 100
Mamdani: 60.00%
Larsen 60.00%
Análisis de los Resultados
De los resultados, se puede observar que los métodos de Mamdani y Larsen obtienen resultados similares. A primera vista no es posible validar si los resultados se asemejan a la realidad, para esto es imprescindible la colaboración de un experto en el tema para la correcta definición de las variables, la asignación de las funciones de membresía más correctas así como la definición de las reglas asociadas.
Conclusiones
En este artículo se muestra cómo utilizar Inferfuzzy, además de demostrar la capacidad de los sistemas de inferencia difusos para abordar problemas donde la definición utilizando la lógica clásica no está clara o donde la solución utilizando esta es demasiado complicada.
Referencias
Sistemas de Control con Lógica Difusa: Métodos de Mamdani y de Takagi-Sugeno-Kang (TSK). Autor: Samuel Diciembre Sanahuja
Temas de Simulación. Autor: Dr. Luciano García Garrido
First Course on Fuzzy Theory and Applications. Autor: Kwang H. Lee
Subscribe to my newsletter
Read articles from leynierdev directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
