The not-so-obvious parallelism inside CPUs
 Coder of the Cellar
Coder of the Cellar
Since the advent of multi-cores x86 CPUs more than 20 years ago, everybody knows that they can do multiple things at once - true multi-tasking instead of the time-slicing trickery - but there are other forms of parallelism that are present, for a longer time, that we can find even inside the original 8086 of 1978.
Each one of these mechanisms has its own peculiarities and recipes to exploit them. I won't spoil them right away, instead we will rediscover them by optimizing a small program that is an ideal candidate for this exercise. The first "hello world" that people do when doing graphics programming, which is the... RGB triangle... The second "hello world" that people do when doing graphics programming, which is the Mandelbrot fractal. An embarrassingly parallel problem, as GPU folks say.
The Mandelbrot Set (you can skip this section)
I won't give much background about this famous fractal, it's stupidly simple yet it generates a truly infinite amount of fascinating details, and you are only limited by your numerical precision and how many iterations you can do, which makes optimization sessions always worth it. Ah yes, at least a first spoiler, even though we will extract some serious performance gains, we won't even get close to a half decent GPU, record breaking Mandelbrot zoomers aren't the topic of today.
Quick remainder, for every point C on the complex plane, we compute an infinite number of times this iteration:
$$\begin{cases} Z_0=0\\ Z_{n+1}=Z_n^2+C \end{cases}$$
There are two possibilities depending on the value of C, either the series diverge to infinity, or not. If not, then all of the Zn stay in the vicinity of the zero forever. These points are the Mandelbrot set. We usually color these points in black, and the others (those that escape to infinity, not part of the Mandelbrot set) with a nice gradient based on the number of iterations it took to be detected as "definitely not part of the set".

The previous iteration can be expressed with real numbers/float variables like this:
$$\begin{cases} X_{n+1}=X_n^2-Y_n^2+C_x\\ Y_{n+1}=2X_nY_n+C_y \end{cases}$$
So the whole program can be written approximately like this:
for (int j = 0; j < HEIGHT; j++) {
for (int i = 0; i < WIDTH; i++) {
float Cx = ... * i + ..., Cy = ... * j + ...;
float Zx = 0.0f, Zy = 0.0f;
int iters = 0;
while (iters < MAX_ITERS && Zx * Zx + Zy * Zy < 4.0f) {
float Zx2 = Zx * Zx, Zy2 = Zy * Zy, ZxZy = Zx * Zy;
Zx = Zx2 - Zy2 + Cx;
Zy = 2.0f * ZxZy + Cy;
iters++;
}
plotPixel(i, j, iters == MAX_ITERS ? 0 : iters);
}}
It can hardly get simpler than that. The important thing to notice is that every pixel can be computed in complete independence from each other, so they can all be processed in parallel. For images that are in mega-pixels, that's millions of independent tasks, more than enough to feed any modern processing unit.
Baseline implementation and benchmark protocol
For testing, I will use this implementation as the reference point, which has some particularities:
#define WIDTH 1024
#define HEIGHT 768
#define ZOOM 0.25f
#define COORD_X -0.25f
#define COORD_Y 0.0f
#define MAX_ITERS 65536
void __attribute__((optimize("-fno-tree-vectorize"))) mandelbrot(int *const restrict buffer) {
const float scale = ZOOM / HEIGHT;
const float Xoffset = COORD_X - 0.5f * ZOOM * WIDTH / HEIGHT;
const float Yoffset = COORD_Y - 0.5f * ZOOM;
for (int j = 0; j < HEIGHT; j++) {
const float Cy = scale * (j + 0.5f) + Yoffset;
for (int i = 0; i < WIDTH; i++) {
const float Cx = scale * (i + 0.5f) + Xoffset;
float Zx = 0.0f, Zy = 0.0f;
int iters = 0;
while (Zx * Zx + Zy * Zy < 4.0f && iters < MAX_ITERS) {
float Zxb = (Zx * Zx + Cx) - Zy * Zy;
float Zyb = (Zx + Zx) * Zy + Cy;
Zx = (Zxb * Zxb + Cx) - Zyb * Zyb;
Zy = (Zxb + Zxb) * Zyb + Cy;
iters += 2;
}
}
buffer[j * WIDTH + i] = iters == MAX_ITERS ? 0 : iters;
}
}
First, in the inner loop, we compute two iterations at once, we unrolled the loop a bit. Tight loops unrolling often improves performance for several reasons, for example because we evaluate less often the loop condition. Here it also allows to write the fractal iterations in a way that better exploit the FMA/MAC units. FMA for Fused Multiply-Add, or MAC for Multiply-Accumulate, which can compute an operation likea * b + c in a single instruction (not a single cycle, but it's still beneficial). The parenthesis mark explicitly how the operations can be mapped to FMAs. Doing so we need to ping-pong between two sets of variables, and that explains why we unrolled the loop a bit. But the main topic here is how to do the same amount of computation faster, not about working smarter/doing less work.
All of the tests have been compiled with GCC 14.1 64 bit, with the following compiler options:
-std=c23 -m64 -march=x86-64-v3 -Ofast -fno-finite-math-only -flto -fopenmp -s
-lgomp
-Ofast is -O3 with -ffast-math, but we disable -ffinite-math-only as with more parallelism we will rely on FP +inf behavior which is broken by -ffast-math.
We also disable the auto-vectorizer of GCC for this function (-fno-tree-vectorize), as GCC will try to vectorize our code, which will bias our comparisons. We'll talk about it at the end.
And if not mentioned otherwise, all the tests are run on a Ryzen 7 5700X3D (8 cores) at a locked 2.8 GHz, with SMT (hyperthreading) disabled. We will discuss about SMT later on.
To make all pixels the same, we zoom into the fractal main cardioid, so all the pixels will run the loop until MAX_ITERS. That way we sidestep the problem of load balancing, so we kind of are in an ideal scenario to try to showcase how much we can gain from each optimization.
Baseline and Thread Level Parallelism
For the baseline implementation, the 1024x768 image has been rendered in 149.3s, almost two and a half minutes. Next, with OpenMP, just adding this one liner:
#pragma omp parallel for schedule(dynamic)
just before the outer loop split the image lines across the 8 cores, and make execution 7.89x faster already (18.92s). Easy and effective. I like OpenMP for this, you take your code as is, just add a small voodoo incantation and it instantly parallelize things across your cores. It can also do some magic stuff when you have some dependencies across your iterations but you have to use the right incantations and need to be extra careful, and it may fail to parallelize and do nothing.
Vectorization, SIMD, AVX, Data Level Parallelism
One of the most advanced usage of OpenMP is to vectorize your code. It's not the first time we talk about vectorization, and it's indeed another form of parallelism. For those who don't really know what this is, you may have already heard of MMX, SSE or AVX. Some execution units inside a core are capable of performing an operation on a full vector at once, for about the same price (Single Instruction, Multiple Data). In case of SSE, these vectors were 128-bit in size, and you could fill them with 4 float numbers, or 2 double, or 16 8-bit integers, etc. With AVX it's the same thing but with 256 bit vectors, so vectors of 8 floats for example.
To best use this in our case, we replace each variable by a vector of those variables, and each operation by the equivalent vector operation. To fill those vectors we simply group together the variables of adjacent pixels. For simplicity here we will split lines of pixels into vectors of 8 pixels.
So we need to modify our program, even if we use OpenMP, and that's where I don't like it as much, you don't really know to what extent you are taking advantage of data level parallelism. There are other alternatives to make your life easier such as OpenCL (provided you can get a good driver for your CPU, which almost doesn't exist for AMD CPUs), Halide, or ispc (wonderful read), but for our simple exercise, I opted for something more direct and explicit, compiler intrinsics. The pain is reduced thanks to GCC vector extension, where the common operators are available on vectors, even in C.
The new multi-threaded and vectorized version now looks like this:
#define WIDTH 1024
#define HEIGHT 768
#define ZOOM 0.25f
#define COORD_X -0.25f
#define COORD_Y 0.0f
#define MAX_ITERS 65536
typedef int Int8 __attribute__((vector_size(32)));
void __attribute__((optimize("-fno-tree-vectorize"))) mandelbrot(Int8 *const restrict buffer) {
const float scale = ZOOM / HEIGHT;
const float Xoffset = COORD_X - 0.5f * ZOOM * WIDTH / HEIGHT;
const float Yoffset = COORD_Y - 0.5f * ZOOM;
#pragma omp parallel for schedule(dynamic)
for (int j = 0; j < HEIGHT; j++) {
const float Cy = scale * (j + 0.5f) + Yoffset;
for (int i = 0; i < WIDTH; i += 8) {
__m256 Cx = scale * (i + (__m256){0.5f, 1.5f, 2.5f, 3.5f, 4.5f, 5.5f, 6.5f, 7.5f}) + Xoffset;
__m256 Zx = {}, Zy = {};
Int8 iters = {}, notFinishedMask = (Int8)_mm256_set1_epi32(-1);
while (_mm256_movemask_ps((__m256)notFinishedMask)) {
__m256 Zxb = (Zx * Zx + Cx) - Zy * Zy;
__m256 Zyb = (Zx + Zx) * Zy + Cy;
Zx = (Zxb * Zxb + Cx) - Zyb * Zyb;
Zy = (Zxb + Zxb) * Zyb + Cy;
iters -= 2 * notFinishedMask;
notFinishedMask = (iters < MAX_ITERS) & (Zx * Zx + Zy * Zy < 4.0f);
}
buffer[(j * WIDTH + i) / 8] = (iters[v] != MAX_ITERS) & iters[v];
}
}
}
We have to realize that for vectorization to work, contrary to multi-threading, every pixel always need to run the exact same instructions of the other pixels that are in the same vector, in sync, which makes fine grained control flow a nightmare. Here each group of 8 pixels needs to run for every pixel until the last one of the group is finished. To avoid unwanted side effects, we use the notFinishedMask to increment the iteration count for the active pixels only. Note that with vector instructions, true is not 1 but all-bits-1, which is -1 for a signed integer, so to increment we subtract with the mask.
In our ideal scenario where there is no execution divergence, in single thread this version also scales very well (18.80s, 7.94x compared to baseline). And with both techniques combined we are down to 2.39 seconds (62.5x).
So here is the results with/without each optimization:
| 1 thread - scalar | 8 threads - scalar | 1 thread - 8 wide | 8 threads - 8 wide |
| 149.3s | 18.92s (7.89x) | 18.80s (7.94x) | 2.39s (62.5x) |
We could pat ourselves in the back, satisfied that the CPU is now properly utilized, but that's still not the case. There is yet another form of parallelism that we neglected, which is...
Instruction Level Parallelism
To understand what is left on the table, we need to talk about super-scalar architectures and pipelining. Both predates multi-cores and vector units which means that what we will see apply for many many CPUs, and even GPUs.
Pipelining has been introduced to split computations into smaller steps, each one could be done faster that the whole computation so frequency could be raised. In the end, the total time to do the same computation (the latency) should merely increase if it takes multiple cycles to execute, while each cycle takes a fraction of what it lasted before. But when one step is done, another instruction can take place in this step, so there can be multiple instructions in the same pipeline, and one instruction can be finished every (short) cycle, thus the effective throughput has been increased.
Super-scalar architectures are just architectures capable of outputting more than one instruction per cycle, for example with multiple ALUs or FPUs. Theoretical 8 (micro-)instructions per cycle are not unheard of on modern architectures.
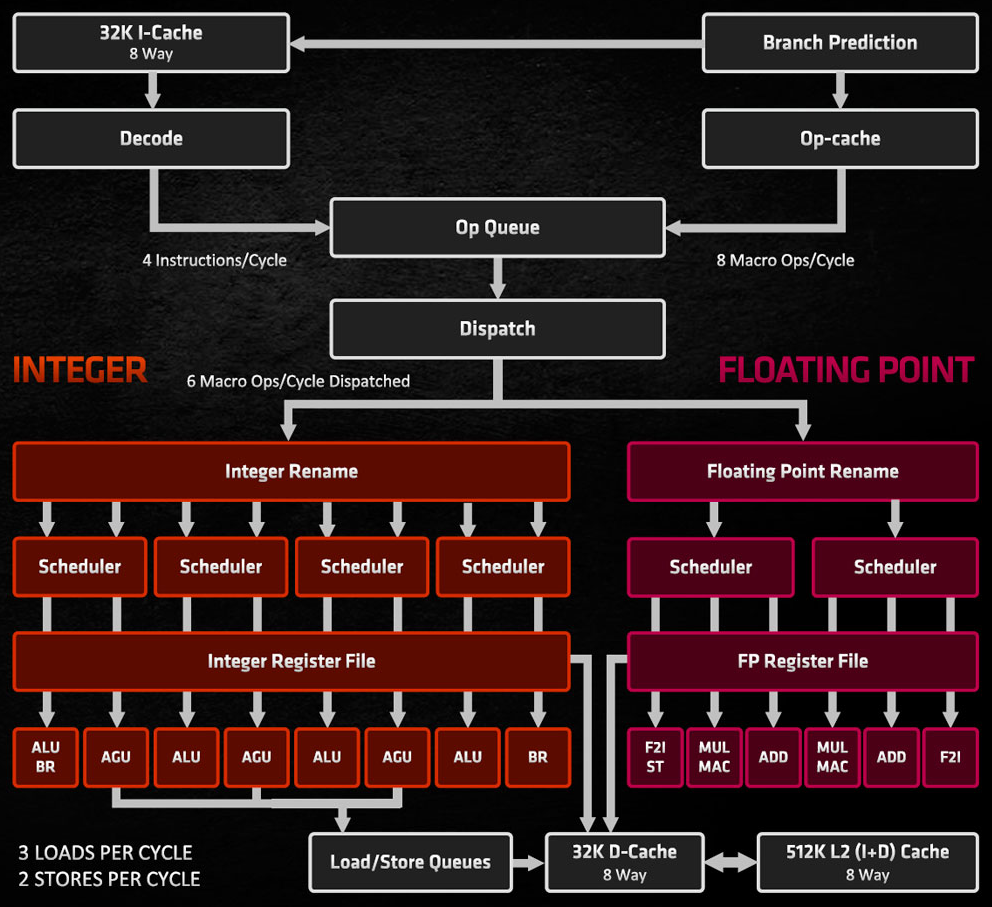
It sounds a nice way to scale the power of a CPU, so why don't we have tens of pipeline stages and ALUs/FPUs? Of all the reasons, the one that interests us here is that an instruction that depends on the result of previous one can't get executed until the previous one has finished its execution. Which means the second instruction can't be scheduled to another available ALU, nor be fed into the pipeline of the ALU where the first instruction still is. So we need to find other instructions which are ready (all of their inputs/preceding instructions have been computed) to not waste precious cycles. Otherwise we say that we introduce "bubbles" into the pipeline.
The number of instructions that are ready at any given cycle is the instruction parallelism of the program, and it's generally not very high and is quite often the limiting factor, as modern CPUs have multiple execution units of each type, each with multiple pipeline stages, that's a lot of parallelism to fill-up too!
So, how do we increase the ILP of our program? We need to increase the number of independent computations inside our inner loop, by adding those of more pixels. So, instead of looping over one set of 8 pixels, we will loop over multiple sets of 8 pixels, "simply" by duplicating our variables and iterations. Again for simplicity we will use the pixels that are on the same line, and we can help ourselves with statically sized loops:
#define WIDTH 1024
#define HEIGHT 768
#define ZOOM 0.25f
#define COORD_X -0.25f
#define COORD_Y 0.0f
#define MAX_ITERS 65536
#define ILP 1
typedef int Int8 __attribute__((vector_size(32)));
void __attribute__((optimize("-fno-tree-vectorize"))) mandelbrot(Int8 *const restrict buffer) {
const float scale = ZOOM / HEIGHT;
const float Xoffset = COORD_X - 0.5f * ZOOM * WIDTH / HEIGHT;
const float Yoffset = COORD_Y - 0.5f * ZOOM;
#pragma omp parallel for schedule(dynamic)
for (int j = 0; j < HEIGHT; j++) {
const float Cy = scale * (j + 0.5f) + Yoffset;
for (int i = 0; i < WIDTH; i += 8 * ILP) {
__m256 Cx[ILP], Zx[ILP] = {}, Zy[ILP] = {};
Int8 iters[ILP] = {}, mask[ILP];
int notfinished;
for (int v = 0; v < ILP; v++) {
Cx[v] = scale * (i + 8 * v + 0.5f + (__m256){0, 1, 2, 3, 4, 5, 6, 7}) + Xoffset;
mask[v] = (Int8)_mm256_set1_epi32(-1);
}
do {
notfinished = 0;
for (int v = 0; v < ILP; v++) {
__m256 Zxb = (Zx[v] * Zx[v] + Cx[v]) - Zy[v] * Zy[v];
__m256 Zyb = (Zx[v] + Zx[v]) * Zy[v] + Cy;
Zx[v] = (Zxb * Zxb + Cx[v]) - Zyb * Zyb;
Zy[v] = (Zxb + Zxb) * Zyb + Cy;
iters[v] -= 2 * mask[v];
mask[v] = (iters[v] < MAX_ITERS) & (Zx[v] * Zx[v] + Zy[v] * Zy[v] < 4.0f);
notfinished |= _mm256_movemask_ps((__m256)mask[v]);
}
} while (notfinished);
for (int v = 0; v < ILP; v++)
buffer[(j * WIDTH + i) / 8 + v] = (iters[v] != MAX_ITERS) & iters[v];
}
}
}
Phew! That requires even more bookkeeping, and it's getting pretty complicated. So, is it worth it?
| ILP | 1 thread - scalar | 8 threads - scalar | 1 thread - 8 wide | 8 threads - 8 wide |
| 1x | 149.3s | 18.92s (7.89x) | 18.80s (7.94x) | 2.39s (62.5x) |
| 2x | 78.49s (1.90x) | 9.94s (15.0x) | 9.91s (15.1x) | 1.26s (118x) |
| 4x | 50.83s (2.94x) | 6.44s (23.2x) | 6.75s (22.1x) | 0.87s (172x) |
| 8x | 48.02s (3.11x) | 6.09s (24.5x) | 7.58s (19.7x) | 0.98s (152x) |
| 16x | 57.99s (2.57x) | 7.37s (20.3x) | 8.08s (18.5x) | 1.03s (145x) |
Well, it seems like there was more bubbles than in a Coca-Mentos! The scaling across the board is very good at double the ILP (~1.9x). At 4x it also shows some nice scaling (~1.5x compared to doubling it) but it seems that we are reaching saturation. Going further ends up decreasing the throughput, probably because the register pressure becomes too high.
With everything combined, we see a total gain of 172x, comfortably under one second! Not bad starting from two and a half minutes! And it could be surprising that there was a potential of 2.75x performance improvement from the last section. And this last optimization can be applied to any processor which is either super-scalar or pipelined.
To sum up, when we are not memory bound like here, to fill up a processor, we need to think about three things: TLP, DLP and ILP, that's the three main forms of parallelism.
What about SMT / Hyperthreading?
Simultaneous Multi-Threading is the ability of a core to decode and execute two threads of instructions at the same time, to feed more independent instructions to the execution units (instructions from two different threads are independent). It's a tool to transform some TLP into ILP.
As there a rule of thumb saying that the complexity of a CPU (transistor count, power consumption) scales quadratically with the "width" of the core (~number of execution units), and due to an intrinsic limit of programs' ILP, there are diminishing returns making wider and wider cores. SMT was a solution to better utilize all of these execution resources, and still providing some gains for lowly threaded programs with a high ILP. So it justified making wider cores.
Now you should be able to guess the effectiveness of SMT. Indeed, "it depends". It should do wonders when the core is starving of independent instructions, but when the executions units are well fed, it shouldn't have much of an impact. So, what are the results with SMT?
| ILP | 16 threads - scalar | 16 threads - 8 wide |
| 1x | 10.07s (14.83x) | 1.25s (119x) |
| 2x | 6.44s (23.18x) | 0.81s (184x) |
| 4x | 5.97s (25.01x) | 0.83s (180x) |
| 8x | 6.16s (24.24x) | 0.95s (157x) |
That's what we are seeing. At low ILP, the SMT improves performance 1.9x, but at high ILP, results are about the same. Though, we reach a new best score of 184x the baseline performance! About the same as going from three minutes to a less than one second, with just 8 cores!
To do so, we had to increase the parallelism of our program 256x (16 threads x 8 wide vectors x 2 ILP), which is 32x per core. That's very similar to the notion of occupancy that is commonplace for GPUs. Though it doesn't mean that we need 32 independent instructions per cycle to feed a CPU core, because the baseline version already had some ILP, we just amplified it by some factors. Thus, the sweet spot should be different for every program, and also for every CPU architecture, the type of data manipulated, etc.
GCC's auto-vectorizer
Remember that we disabled it for all the tests, because under the right circumstances, GCC can transform our scalar code to vector code all by itself. Here are my results with the auto-vectorizer enabled, on the scalar version, with 8 threads, and varying the ILP:
| ILP | scalar - auto-vectorizer OFF | scalar - auto-vectorizer ON | 8 wide |
| 1x | 18.92s | 18.89s | 2.39s |
| 2x | 9.94s | 9.95s | 1.26s |
| 4x | 6.44s | 6.45s | 0.87s |
| 8x | 6.09s | 6.08s | 0.98s |
| 16x | 7.37s | 1.34s | 1.03s |
| 32x | 1.18s | ||
| 64x | 1.37s |
Up to 8x ILP, there is no difference, but suddenly starting from 16x ILP, GCC manages to do a pretty good job at vectorizing the code. I don't know why it doesn't kicks-in sooner but the results are better than what I expected.
What next?
As I said in the intro, all this has limited practical purposes. It's hard to find problems that offer enough parallelism to completely fill a CPU that don't map well to GPUs, which would easily obliterate a similarly priced CPU. And it's a lot easier too as the GPU programming models hides the mapping of TLP and DLP to the hardware. And even if good ILP can help on some difficult situations, you can often get away with a bad one if you have a good occupancy.
But one weak point of consumer grade GPUs is other data types than 32 bit floating point numbers, particularly 64 bit / double precision which runs at 1/32th the throughput of floats on most Geforces. So I may write a follow up to assess the balance of power between CPUs and GPUs on doubles, it might be interesting!
Subscribe to my newsletter
Read articles from Coder of the Cellar directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Coder of the Cellar
Coder of the Cellar
Codeur du Cellier