Precedence and Associativity in Grammar Rules

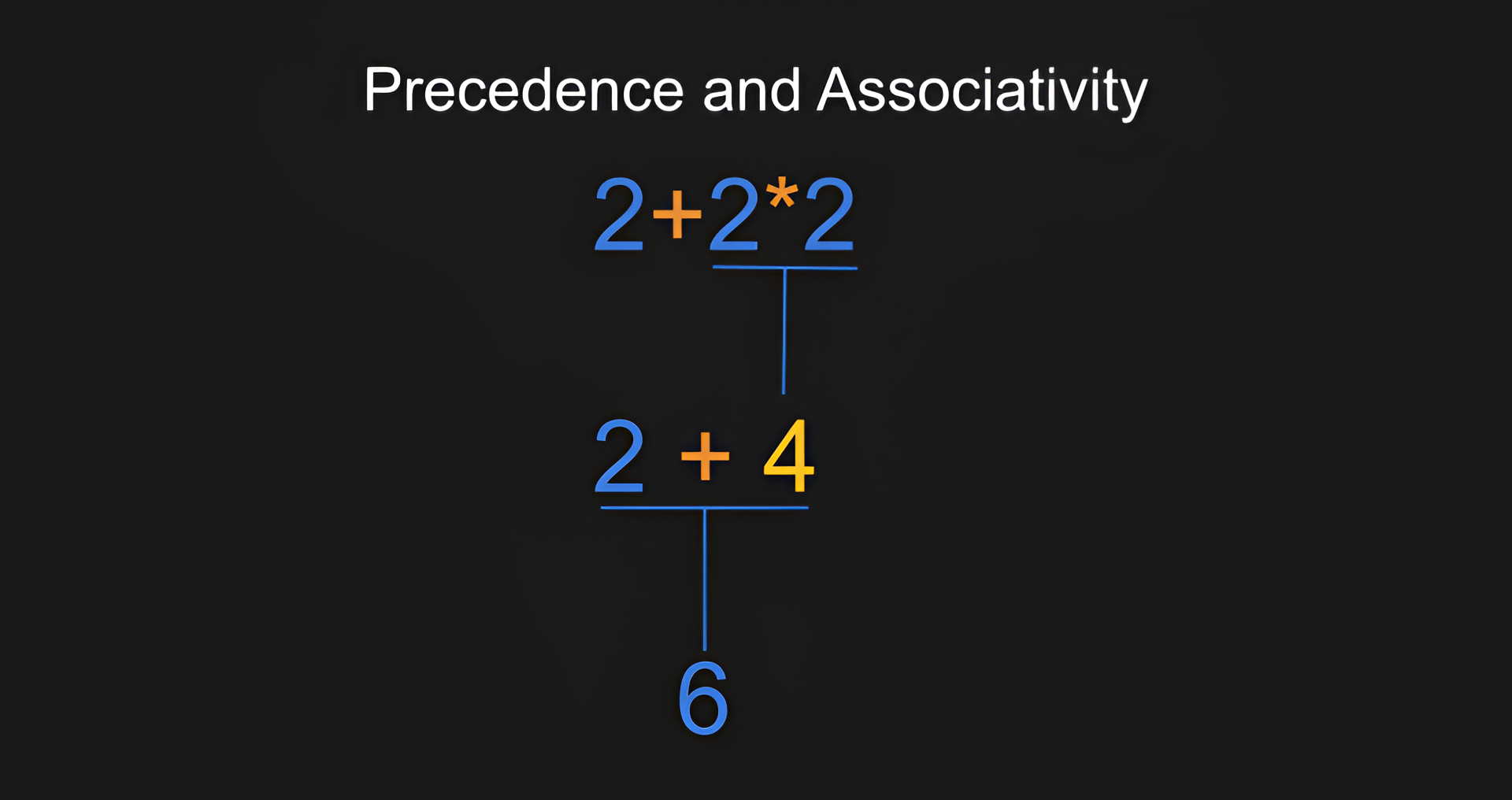
Previous Posts:

Creating TuffScript: Exploring Esoteric Programming Languages and Their Foundations

Mastering Formal Grammars: An Introduction to the Chomsky Hierarchy

Precedence And Associativity

Let's talk a bit about precedence and associativity.

Precedence determines the order of operations in an expression. Higher precedence operations are performed before lower precedence ones.

Associativity defines the direction in which operations of the same precedence are evaluated.

Left-associative operations are evaluated from left to right, while right-associative operations are evaluated from right to left.

Left Associativity (Addition):

• Expression: 2 + 3 + 4

• Left-associative addition evaluates from left to right:

  • First, it adds 2 + 3 as 5.

  • Then, it adds 5 + 4 as 9.

Right Associativity (Exponentiation):

• Expression: 2 ^ 3 ^ 2

• Right-associative exponentiation evaluates from right to left:

  • First, it evaluates 3 ^ 2 as 9.

  • Then, it evaluates 2 ^ 9 as 512.

Essentially, right-associativity means that when you have multiple consecutive "^" operators, the calculation starts from the rightmost one and works its way to the left.

In both cases, associativity determines the order in which operations are performed when they have the same precedence.

The way a BNF (Backus-Naur Form) grammar is written can implicitly define both the precedence of operations and their associativity in arithmetic expressions. Let's see how this is achieved using the grammar we created earlier:

<expression> ::= <term> | <expression> + <term> | <expression> - <term>

<term> ::= <factor> | <term> * <factor> | <term> / <factor>

<factor> ::= <number> | ( <expression> )

<number> ::= <digit> | <number> <digit>

<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Precedence: The precedence of operations is determined by the structure of the grammar rules and how they nest. For instance, in the grammar of arithmetic expressions:

• The <expression> rule includes addition and subtraction, and it refers to <term>.

• The <term> rule, which is a part of the <expression> rule, includes multiplication and division, and it refers to <factor>.

• This structure means that operations in <term> (multiplication and division) have higher precedence than those in <expression> (addition and subtraction) because the <term> is evaluated first as part of evaluating an <expression>.

Associativity: The associativity of operators in a grammar is determined by the position of the recursive part of the rule: on the left for left associativity, and on the right for right associativity. In the same grammar of arithmetic expressions:

• For the rule <expression> ::= <term> | <expression> + <term> | <expression> - <term>, the recursion is on the left side (<expression> on the left of '+'). This implies left associativity for addition and subtraction. It means when you have an expression like a + b - c, it is interpreted as (a + b) - c.

• Similarly, for the rule <term> ::= <factor> | <term> * <factor> | <term> / <factor>, the recursion on the left side indicates left associativity for multiplication and division. So, a * b / c is treated as (a * b) / c.

The way these rules are crafted is crucial for ensuring that expressions are parsed and evaluated correctly according to the conventional rules of arithmetic.

Let's see how it would look if we had an exponentiation operator.

To include an operator like "^" (exponentiation) in the BNF grammar for arithmetic expressions, we need to consider both its precedence and associativity. Generally, exponentiation has a higher precedence than multiplication and division and is right-associative. Here's how you can modify the grammar to include exponentiation.

Since exponentiation has a higher precedence than multiplication and division, it should be placed at a level above <term> in the hierarchy. We'll introduce a new rule <power> to handle this:

<expression> ::= <term> | <expression> + <term> | <expression> - <term>

<term> ::= <power> | <term> * <power> | <term> / <power>

<power> ::= <factor> | <factor> ^ <power>

<factor> ::= <number> | ( <expression> )

<number> ::= <digit> | <number> <digit>

<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Let's analyze it step by step:

1. <power> ::= <factor> | <factor> ^ <power>:

   • The <power> construct can be either a single <factor> or a <factor> followed by a "^" operator and another <power>.

2. <factor> ^ <power>:

   • The key aspect here is the position of the recursion in the rule <factor> ^ <power>. The recursive part (<power>) is on the right side of the "^" operator. This right-sided recursion is what leads to the right associativity of the power operator.

To understand why the right recursion leads to right associativity, consider how an expression like 2 ^ 3 ^ 4 would be parsed with our grammar:

• First, the expression matches the pattern <factor> ^ <power>, with 2 as <factor> and 3 ^ 4 as <power>.

• Then, the 3 ^ 4 part is itself a <power> and is parsed again as <factor> ^ <power>.

• This process results in the expression being effectively grouped as 2 ^ (3 ^ 4).

Thus, the right recursion forces the operations to be grouped from right to left.

By introducing a separate rule for exponentiation and positioning it correctly in the hierarchy of operations, we ensure that it has the appropriate precedence and associativity. This modified grammar now supports exponentiation along with the other basic arithmetic operations, following the conventional rules of arithmetic.

Ambiguity

One interesting property of grammars is their relationship to ambiguity.

Ambiguity in grammar occurs when a single string can be generated through more than one leftmost or rightmost derivation, resulting in the same sentence having multiple parse tree (or derivation trees). Since we already understand the logic behind leftmost and rightmost derivations, we can discuss some examples of ambiguous grammars. In the future, we will learn what a parse tree is and how to construct it.
Let's look at this example of ambiguous grammar:

1. S → aA | aB

2. A → c

3. B → c

This grammar is ambiguous because it allows for the generation of the same string through different production paths. Specifically, both productions S → aA and S → aB can lead to the string "ac" by following either path: S → aA → ac or S → aB → ac. The ambiguity arises because there are two different derivation sequences that produce the same string, making it unclear which derivation path was intended for "ac".

Let's examine another example of ambiguous grammar:

1. S → S

2. S → ε

Here, "S" is the start symbol (or nonterminal), and ε represents the empty string (a string with no characters):

1. Rule 1 (S → S) says that the nonterminal "S" can be replaced by itself.

2. Rule 2 (S → ε) says that "S" can also be replaced by the empty string.

The ambiguity arises because there are multiple ways to derive the same string (in this case, the empty string) from this grammar. For instance, to derive the empty string, you can apply Rule 2 directly to the start symbol "S" to get ε. However, you can also first apply Rule 1 any number of times (which keeps the string as "S" since it replaces "S" with itself), and then apply Rule 2 to finally derive ε. This means there are infinitely many derivations for the empty string, each with a different number of applications of Rule 1 before Rule 2 is applied. This is what makes the grammar ambiguous.

Let's now see the unambiguous version of the same grammar:

1. S → ε

In this simpler grammar, there's only one rule, which directly replaces the start symbol "S" with the empty string ε.

This grammar is unambiguous because there's only one possible way to derive the empty string from the start symbol "S". There are no alternate paths or choices in the derivation process. The empty string is produced in a single step, without any possibility for variation or multiple interpretations.

If we take a look at the arithmetic expressions grammar that we defined earlier, it is unambiguous. It respects the conventional precedence and associativity of arithmetic operations.

We can try to define an ambiguous version of the grammar for arithmetic expressions. So, we need to design rules that allow for more than one way to derive strings (creating multiple parse trees) for the same expression. Ambiguity typically arises when the grammar does not clearly define operator precedence or associativity, or when it allows multiple ways to derive the same string of symbols.

Here's an example of an ambiguous grammar for arithmetic expressions:

<expression> ::= <expression> + <expression>

| <expression> - <expression>

| <expression> * <expression>

| <expression> / <expression>

| <expression> ^ <expression>

| ( <expression> )

| <number>

<number> ::= <digit> | <number> <digit>

<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

In this grammar no separate rules exist for different precedence levels. In the grammar, all operators (+, -, *, /, ^) are treated at the same level, implying that it does not enforce any operator precedence.

There is also a lack of definition regarding associativity. Since all operations are defined uniformly, the grammar does not specify whether the operators are left-associative or right-associative.

Examples of Ambiguity:

• Consider the expression 3 - 2 - 1. This could be parsed as either (3 - 2) - 1 or 3 - (2 - 1), leading to different results.

• The expression 2 ^ 3 ^ 2 could be interpreted as either (2 ^ 3) ^ 2 or 2 ^ (3 ^ 2), again leading to different outcomes.

• The expression 3 + 4*5 does not inherently prioritize multiplication over addition. Without precedence rules, it's unclear whether this should be parsed as (3 + 4)*5 or 3 + (4 * 5).

• Even with parentheses, certain expressions could be ambiguously parsed due to the lack of precedence rules.

Let's imagine that we're trying to generate the string "5 + 5 * 5".

Based on our grammar, we can do it like this:

1. <expression>

2. <expression> + <expression>

3. <number> + <expression>

4. <number> + (<expression> * <expression>)

5. <number> + (<number> *<expression>)

6. <number> + (<number>*<number>)

Or we can do it another way:

1. <expression>

2. <expression> * <expression>

3. (<expression> + <expression>) * <expression>

4. (<number> + <expression>) * <expression>

5. (<number> + <number>) * <expression>

6. (<number> + <number>) * <number>

You can see that using the leftmost derivation, we can construct the same string in at least two different ways.

In summary, this grammar is ambiguous because it does not clearly specify the precedence and associativity of operators, allowing for multiple valid parse trees for the same expression. In practical scenarios, such ambiguity is undesirable, as it leads to confusion and inconsistency in how expressions are evaluated.

Understanding and identifying ambiguity in grammars is an important concept in the fields of computer science, especially in compiler design and programming language development.

Detecting ambiguity in grammars, especially in context-free grammars (CFGs), is a complex and challenging task. Unfortunately, there's no general-purpose tool that can automatically and reliably detect ambiguity in any given CFG. The problem of deciding whether a general context-free grammar is ambiguous is undecidable, which means there's no algorithm that can determine ambiguity for all possible grammars in a finite amount of time. It has been proven that no such algorithm can exist. The reasoning behind this proof is linked to the Post Correspondence Problem, an undecidable decision problem. The key idea is that this problem can be represented using a Context-Free Grammar (CFG). This establishes a connection between identifying ambiguity in CFGs and determining the outcome of the Post correspondence problem, which is undecidable. Consequently, the ambiguity of a CFG is also undecidable. You can check out this video on YouTube from the Easy Theory channel, which describes the main concepts related to this topic.

In practice, finding and fixing ambiguities in programming language grammars involves a combination of methods. Developers often use parser tools to identify common issues, and manually examine grammars to spot particularly tricky areas. Automated tests are also valuable, as they can highlight problematic parts. Although no single tool can catch every ambiguity, combining these approaches is generally effective in most situations.

Semantics

I also want to talk a bit about semantics. We need to remember that semantics refers to the meaning of a language construct, while grammar defines how constructs are formed. Grammar is like the syntax or structure of a language, dictating how words and symbols can be combined. Semantics, on the other hand, is concerned with what these combinations mean. In programming, for instance, grammar might allow you to write "a + b", but semantics determines what this addition operation actually does. In summary, grammar is about structure; semantics is about meaning. They are related but distinct aspects of language.

Conclusion

Understanding how precedence and associativity work at the grammar level is important. It is also important to distinguish between grammar and semantics. We'll dive into the details of the syntax analysis phase in the upcoming series, so stay tuned!