Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) is a cornerstone algorithm in the realm of machine learning. Its simplicity, efficiency, and effectiveness have made it a go-to choice for optimizing a wide range of models, from linear regression to deep neural networks.

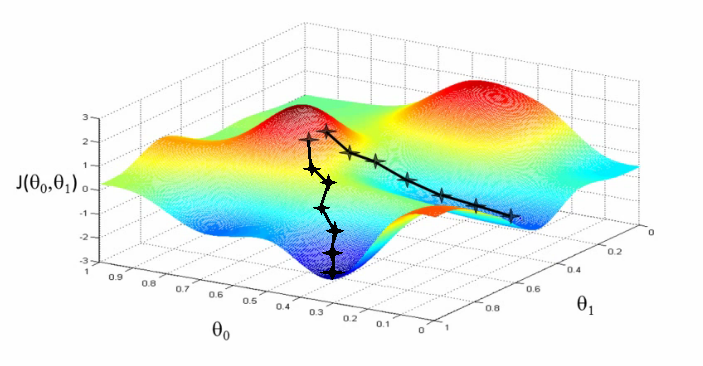
Understanding Gradient Descent

Before diving into SGD, it's essential to grasp the concept of gradient descent. Imagine a hiker trying to find the lowest point in a valley. They would take steps in the direction of the steepest descent. Gradient descent works similarly, iteratively moving towards the minimum of a function.

In the context of machine learning, the function is often a loss function, measuring the error between predicted and actual values. Gradient descent aims to minimize this loss function by adjusting model parameters in the direction of the steepest descent of the error surface.

The Birth of Stochastic Gradient Descent

While gradient descent is effective, it can be computationally expensive for large datasets. This is where Stochastic Gradient Descent (SGD) comes into play. Instead of calculating the gradient for the entire dataset in one iteration, SGD randomly selects a single data point or a small batch of data points to compute the gradient.

This approach offers several advantages:

• Computational Efficiency: By processing data in smaller chunks, SGD reduces memory requirements and speeds up training.

• Flexibility: SGD can be used for online learning, where data arrives in a stream.

• Escape from Local Minima: The stochastic nature of SGD can help the algorithm escape local minima, which are suboptimal solutions.

    import numpy as np
    from sklearn.linear_model import SGDClassifier
  
    # Sample data (replace with your data)
    X = np.array([[1, 2], [2, 3], [3, 1], [4, 3]])
    y = np.array([0, 1, 1, 0])
  
    # Create an SGD classifier
    clf = SGDClassifier(loss='hinge', penalty='l2', max_iter=1000)
  
    # Train the model
    clf.fit(X, y)
  
    # Make predictions
    predictions = clf.predict(X)
  

How SGD Works

The SGD algorithm iteratively updates model parameters based on the gradient of the loss function calculated for a randomly selected data point or batch. The update rule is typically:

theta = theta - learning_rate * gradient

Where:

• theta is the model's parameters

• learning_rate is a hyperparameter controlling the step size

• gradient is the gradient of the loss function with respect to the parameters

Challenges and Improvements

While SGD is efficient, it has some drawbacks:

• Oscillations: Due to the stochastic nature, the optimization path can be noisy, leading to oscillations.

• Learning Rate: Choosing the optimal learning rate is crucial for convergence.

• Local Minima: SGD can get stuck in local minima, especially in complex landscapes.

To address these issues, several variants of SGD have been developed:

• Mini-batch Gradient Descent: Uses small batches of data to reduce noise and improve convergence.

• Momentum: Accumulates past gradients to accelerate convergence and dampen oscillations.

• AdaGrad: Adapts the learning rate for each parameter, speeding up convergence.

• Adam: Combines the best aspects of AdaGrad and RMSprop, offering adaptive learning rates.

SGD in Deep Learning

SGD and its variants are the workhorses behind training deep neural networks. They enable efficient optimization of millions of parameters. Techniques like backpropagation and chain rule are used to compute gradients, which are then used to update network weights.

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# Sample data (replace with your data)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess data
x_train = x_train.reshape(60000, 784) / 255.0
x_test = x_test.reshape(10000, 784) / 255.0

# Create a simple model
model = Sequential([
    Dense(512, activation='relu', input_shape=(784,)),
    Dense(10, activation='softmax')
])

# Compile the model
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=['accuracy'])

# Train the model
model.fit(x_train, y_train, epochs=5, batch_size=32)

Conclusion

Stochastic Gradient Descent is a fundamental algorithm in machine learning with a profound impact on the field. Its ability to handle large datasets efficiently, coupled with its adaptability, has made it a cornerstone of modern deep learning. While challenges exist, the ongoing research and development in optimization algorithms continue to improve the performance and robustness of SGD.

Thank you for reading till here. If you want learn more then ping me personally and make sure you are following me everywhere for the latest updates.

Yours Sincerely,

Sai Aneesh

x.com/lhcee3

linkedin.com/in/saianeeshg90