The Dynamics of DEX Arbitrage: Practical Strategies and Mathematical Insights
 Aleksei Babenkov
Aleksei Babenkov
Introduction
Hello. I’m Aleksei Babenkov, an experienced researcher specializing in machine learning and high-frequency trading. With over eight years in the field, including leadership roles at MaximaTelecom and Avito, I’ve recently shifted my focus to quantitative research. My current work involves exploring algorithmic trading and building high-frequency trading (HFT) robots, combining my expertise in decentralized finance, mathematics, and algorithms.
Understanding Arbitrage
Arbitrage is one of the fundamental laws of economics. When something is cheaper on one market and more expensive on another, arbitrageurs buy on the cheaper market and sell on the more expensive one. This process balances prices across markets naturally, without the need for complex synchronization systems.
Arbitrageurs are crucial in financial markets. They:
Help equalize prices across platforms
Contribute to liquidity
Reduce price volatility
Enhance market stability
However, traditional arbitrage faces challenges, particularly the risk of non-atomicity on centralized exchanges (CEXs).
Decentralized Exchanges (DEX) Basics
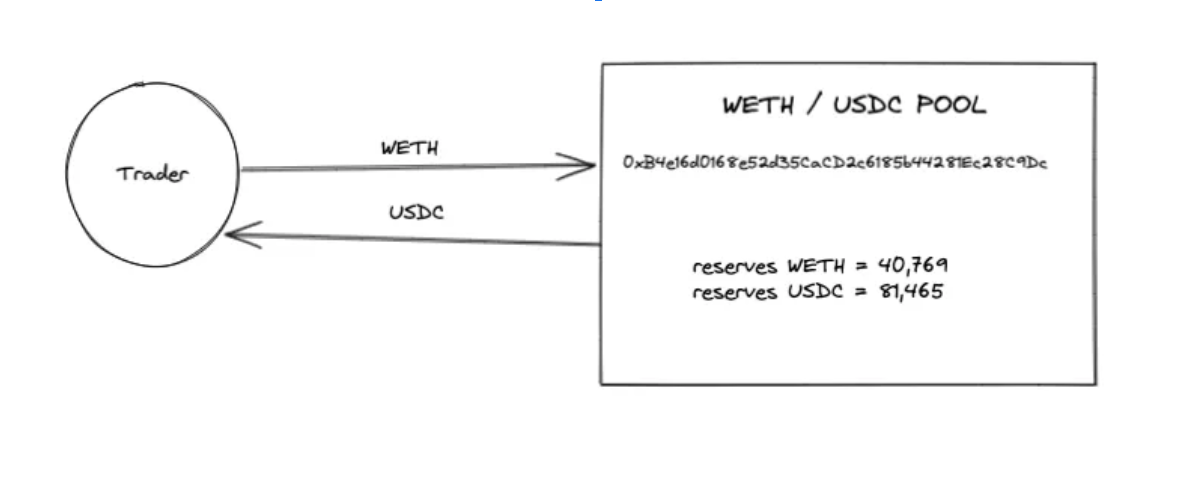
Decentralized exchanges (DEXs), unlike centralized exchanges (CEXs), use an Automated Market Maker (AMM) model, which allows for peer-to-peer transactions directly on the blockchain, eliminating the need for intermediaries. Let’s focus on UniswapV2 as an example, as its simplicity helps in understanding the basics of DEXs.
You might be wondering, “Isn’t UniswapV2 outdated and less effective?” While newer versions like UniswapV3 offer more advanced features, many forks of UniswapV2 are still actively used today. The simplicity of UniswapV2 makes it an excellent example for understanding the basics. Its pricing function is just a few lines of code, compared to the over 1,000 lines in UniswapV3. This simplicity helps us grasp the core concepts without getting bogged down in complexity.
At the heart of UniswapV2 is the concept of liquidity pools. These pools are collections of funds provided by users, known as liquidity providers, who deposit pairs of assets into the pool. In return, they receive liquidity tokens representing their share of the pool, which can be redeemed for the underlying assets plus a portion of the trading fees.
UniswapV2 uses a constant product formula, x⋅y=k, where x and y represent the quantities of two assets in the pool, and k is a constant. This formula ensures that the product of the quantities remains the same before and after a trade, maintaining balance in the pool.
When a user wants to swap one asset for another, they interact with the smart contract, which calculates the exchange rate based on the current reserves in the pool. The swap adjusts the reserves, ensuring that the constant product formula holds. This atomic nature ensures that either all steps succeed, or none do, minimizing the risk to gas fees.
Programmatically, a DEX is essentially a collection of trading pairs. Each pair can be thought of as a class in Solidity, the language used for writing smart contracts. These classes have reserves of two currencies. When you want to trade, the pair takes one currency from you, adds it to the reserve, and gives you an equivalent amount of the other currency, minus a small transaction fee.
DEX Arbitrage Mechanics
DEX arbitrage leverages the atomic nature of transactions, which means all steps in the arbitrage process either succeed or none do. This minimizes the risks traditionally associated with arbitrage, such as losing money due to partial transaction failures.
While our earlier example of UniswapV2 provides a good foundation, real-world DEX arbitrage is much more complex. Successful strategies often involve trading across different types of decentralized exchanges (DEXs). For example, you might buy on UniswapV2 and sell on UniswapV3 or Algebra.
The complexity varies significantly between DEXs. UniswapV2 uses simple, formulaic pricing functions, whereas other DEXs may have complex logic and iterative pricing mechanisms with thousands of lines of code. Additionally, most DEXs do not have smooth, easily differentiable pricing functions, which makes traditional optimization techniques less effective.
Despite these complexities, a universal principle applies: price impact. In all DEXs, larger trade volumes result in worse average prices. This fundamental economic law allows us to generalize our strategies, even when faced with diverse and complex exchange mechanisms. By understanding and leveraging this principle, we can adapt our arbitrage approach to work across various DEX types, maximizing opportunities in the diverse landscape of decentralized finance.
Mathematical Foundations of DEX Arbitrage
At the core of UniswapV2 is the pricing function, getAmountOut, which determines the output tokens for a given input based on a constant product formula. The formula for getAmountOut is:
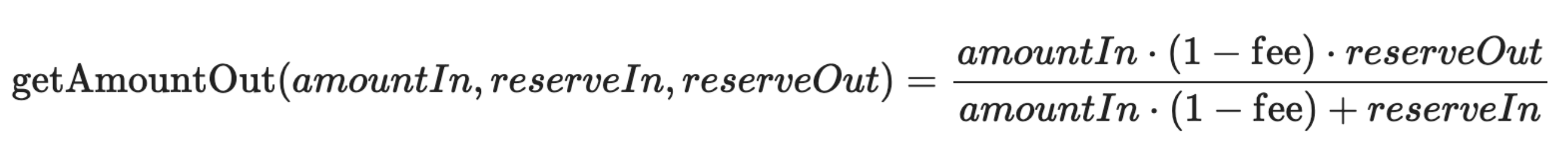
Where:
a is the input amount,
r_in and r_out are the reserves of the input and output tokens, respectively,
f represents the fees.
This formula has two key properties:
Nonlinearity: Larger trades result in diminishing returns.
Natural liquidity limit: The last token in reserve would theoretically cost an infinite amount.
To understand arbitrage opportunities, it’s convenient to transform our problem into a formal and tractable mathematical object. Suppose we have two trading pairs, each with its own reserves and fees. Our goal is to determine if there is an arbitrage opportunity between these pairs. We construct a profit function to evaluate this:
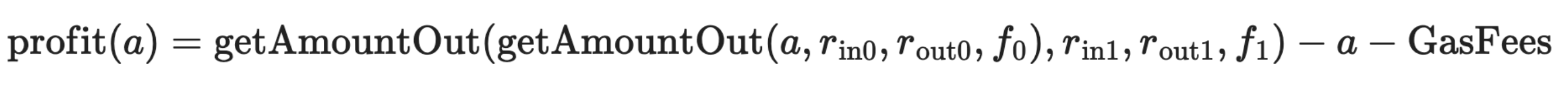
Where a is the input amount, r_in and r_out are reserves, and f represents fees for pairs with indices 0, 1 in the order they are traded (first on pair 0, then on pair 1).
The left plot shows the output amount after two swaps (blue curve) compared to the input amount (red dashed diagonal). The right plot displays the profit function profit(a), highlighting the input amount where the profit is maximized (red cross) and where it is zero (blue cross). The green shaded area represents the positive profit zone, indicating where arbitrage opportunities are profitable. The unimodal shape of the profit function illustrates the optimal trade volumes for maximizing profit.
For UniswapV2, we can find the optimal trade volume analytically because the formula is straightforward. By taking the derivative of the profit function and setting it to zero, we can solve for the maximum. I’ll leave this exercise to the reader.
For other, more complex DEXs, there isn’t a simple formula like UniswapV2’s getAmountOut. Instead, these DEXs use algorithms to compute prices. However, the principle of price impact still applies, providing us with a crucial insight. Larger trade volumes result in worse average prices, which we can exploit.
Despite the lack of a simple formula, this problem can still be tackled using numerical optimization methods that do not require knowledge of the derivative. These methods allow us to find the optimal trade volume efficiently, even in the absence of an explicit formula.
The profit function itself has interesting theoretical properties. Its nonlinearity introduces challenges but also provides opportunities for optimization. The shape of the profit function can often be unimodal, meaning it has a single peak. This makes it suitable for optimization techniques that seek to find this peak effectively.
Historically, the concept of optimization in financial markets has evolved significantly. Early arbitrage strategies were often straightforward and relied on manual calculations. With the advent of electronic trading, the need for more sophisticated mathematical models became apparent. Today, the integration of numerical methods and algorithmic trading allows for real-time optimization, making arbitrage a highly competitive field.
Finding Arbitrage Opportunities
Now that we can calculate profit and detect arbitrage opportunities, the question arises: how do we construct the initial set of candidate pairs to check? Arbitrage can be visualized as cycles in a graph of tokens and pairs. We use depth-first search (DFS) to detect these cycles efficiently. While computationally intensive, this process doesn’t need frequent updates, only when trading pairs change.
Arbitrage Algorithm
Compute set of paths (pre-computation)
Main loop:
Receive price updates
Iterate through paths
Calculate optimal amounts
Select best path(s)
Execute arbitrage transaction
Repeat
This framework provides the foundation for DEX arbitrage, but real-world implementation requires additional sophistication and optimization.
Real-World Challenges and Advanced Strategies
In practice, the basic framework we’ve discussed isn’t enough. Competition is fierce in the world of DEX arbitrage, and to succeed, we need to be smarter and more innovative. Some traders may have advantages like partnerships with validators, but the primary challenge comes from the high level of competition itself.
Performance Considerations
When tackling DEX arbitrage, one of the main challenges is the sheer size of the search space. For instance, if you try to index Binance Smart Chain (BSC) and find all possible paths, you could potentially end up with tens of billions of paths. As the number of potential trading paths grows exponentially with the size of the graph, we need effective strategies to prune this search space and focus on the most promising opportunities.
Limit Cycle Lengths: Paths longer than four swaps are rarely profitable. By capping the cycle lengths to four or fewer steps, we significantly reduce the search space and computational load, allowing for more efficient and effective analysis.
Time Constraints: We need to limit the algorithm’s run time. This involves not only setting a time constraint just under the average block time but also designing the algorithm to always know its best hypothesis at any given moment. Given these strict limitations, our algorithm must be prepared to be interrupted at any time and still be able to provide a viable result.
Upper Bound Calculations: We can calculate an upper bound for profit using basic mathematical operations. If this upper bound is less than zero, we can skip the optimization for that path entirely. This approach helps us avoid wasting computational resources on unprofitable paths.
Path Ranking: Prioritizing paths with higher probabilities of yielding opportunities is crucial. Because we can’t evaluate every possible path, ranking paths based on their likelihood of success helps us focus our efforts on the most promising candidates. This can be done using heuristics, historical data, or even machine learning models trained to identify profitable paths.
Network-Specific Dynamics
Networks can be categorized into three types based on their transaction prioritization:
No gas auction (e.g., Telos): First-In-First-Out principle
Gas auction with paid reverts: Traders bid on transaction priority
Gas auction with free reverts (e.g., BSC, Ethereum): Extremely competitive due to reduced risk
Types of Network and Competition Rules
| Network Type | Example | Description | Competition Type |
| No Gas Auction | Telos EVM | No manual gas price, FIFO | Speed is the key, first transaction wins |
| Gas Auction with Paid Reverts | Most of the nets | You have to pay gas even if the transaction reverts. Fee depends on your bid | Highest bid wins, you have to pay for your priority, keeping risks in mind |
| Gas Auction with Free Reverts | Ethereum, BSC, Polygon | Arbitrageurs use services like MEV-Builders, Flashbots, etc | Aggressive bidding(up to 99.9% of reward), highest competition because of absolutely no risks |
Advanced Bidding Strategies
On most networks, simply identifying an arbitrage opportunity isn’t enough. You also need to place the right bid (set a gas price) to ensure you win the transaction. Your goal is to set the minimum gas price that’s still higher than your competitors, thereby winning this “gas auction.”
Bid Multiples of Base Gas Price: One common approach is to bid a multiple of the base gas price, often denoted as base price times X. This straightforward strategy ensures that your bid is competitive without overpaying.
Bid Fixed Increments Above Base Price: Another approach is to bid a fixed increment above the base price. This can be effective in stable, low-competition environments, where the gas prices are relatively predictable.
Bid Percentage of Expected Profit: A more sophisticated strategy involves bidding a percentage of the expected profit from the arbitrage opportunity. For instance, you might bid a fixed percentage of the profit, such as 50%. This approach directly ties the gas cost to the profitability of the trade, ensuring you don’t overpay for transactions with lower expected returns.
Dynamic Approach with Upper Limits and Fallback Strategies: For an advanced variant, you can use a dynamic approach where you bid a percentage of the profit but set an upper limit on the gas price. For example, you might bid 50% of the expected profit, but if this results in a gas cost exceeding a certain threshold, you cap the bid at that threshold. If the transaction cost still seems too high, you fallback to a simpler strategy like base price times Y.
Monitor and Outbid Competitors: More advanced strategies involve closely monitoring your competitors’ bids. The logic here is simple: to win, you need to bid just enough to outbid your competition without significantly reducing your profit margin. One effective method is to set your bid slightly above the last successful bid from your top competitor. For instance, if your competitor made a profit with a gas price of 100 gwei, you might bid 105 gwei. This incremental approach keeps you competitive while avoiding unnecessary costs.
Leveraging Machine Learning
Machine learning can significantly enhance our arbitrage strategies in various ways:
Hybrid Bidding Strategy
By collecting historical data on your bids and those of your competitors, we can train predictive models to forecast the winning bid. This model can help determine the lowest gas price necessary to win the transaction, significantly improving our bidding efficiency. This approach mixes various bidding strategies, allowing us to adapt dynamically to market conditions.
Transaction Selection
In the raw version of our algorithm, we select paths that maximize the profit function. However, this function only estimates the potential profit from price differences and doesn’t account for the level of competition and our chances of winning. Machine learning helps us refine this by calculating the expected profit, which considers both potential profit and the probability of winning. By incorporating competition levels, we can prioritize paths with a lower profit but a higher chance of success, ultimately yielding greater returns over time.
Flash Loans in Arbitrage
Flash loans are an exciting concept that can amplify your arbitrage opportunities without needing significant capital. They allow you to borrow large amounts of cryptocurrency without collateral, provided you repay the loan within the same transaction block. This unique feature of decentralized finance enables you to use borrowed funds to execute arbitrage, capturing price differences across DEXs, and then repaying the loan with the profits.
Here’s how it works in practice:
Borrowing Funds: You initiate a flash loan to borrow the necessary amount of tokens.
Executing Arbitrage: With the borrowed funds, you perform arbitrage by swapping tokens across different DEX pairs to capture price differences.
Repaying the Loan: After completing the swaps, you repay the flash loan with the borrowed amount plus any fees.
The beauty of flash loans lies in their risk management. If the arbitrage transaction is not profitable, you only need to cover the gas fees, as the entire transaction will revert if the loan is not repaid. This dramatically reduces both the risk and the capital requirement, making high-volume trades accessible even without a large amount of upfront capital.
Flash loans open up a world of possibilities for arbitrage traders, leveraging the programmable nature of smart contracts to execute complex trading strategies atomically
Conclusion
DEX arbitrage presents unique challenges, often more complex than classical high-frequency trading. It requires efficient code writing and optimization. However, it’s still possible for talented individual programmers to succeed without backing from large companies.
The combination of understanding DEX mechanics, advanced mathematical modeling, strategic thinking, and innovative approaches like machine learning can lead to successful arbitrage strategies in the dynamic world of decentralized finance.
Subscribe to my newsletter
Read articles from Aleksei Babenkov directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Aleksei Babenkov
Aleksei Babenkov
ML HFT Quant Researcher