Data Structure : Introduction to Trie
 Fatima Jannet
Fatima Jannet
A Trie is a tree-based data structure that organize information in a hierarchy. The main point is, while most other structures are designed to manipulate data, trie is often used with strings.
Properties:
It is typically used to store or search strings in a space, time efficient way
Any node in trie can store non-repetitive multiple characters.
Every node stores link of the next character of the string.
Every node keeps track of 'end of string'
Visualization:
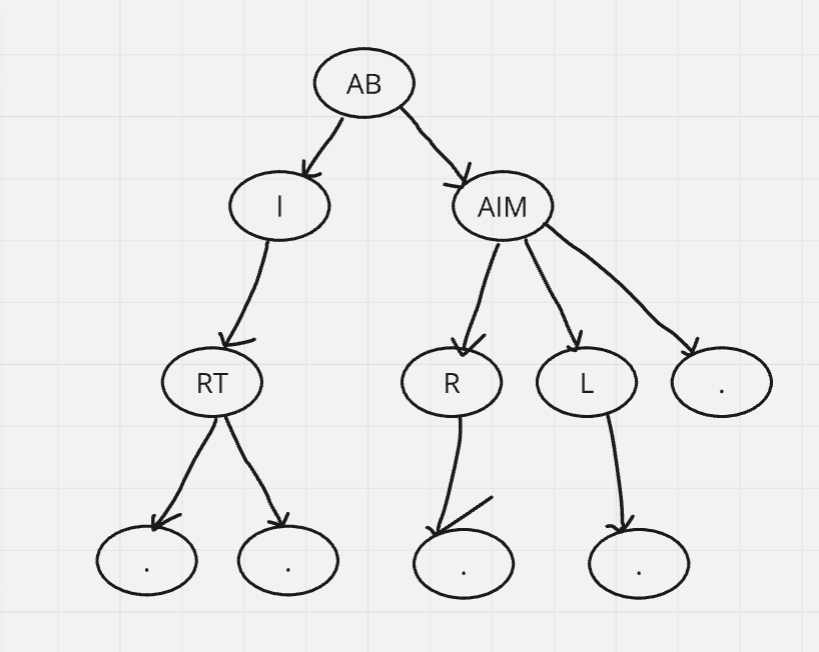
A typical trie looks like this. Look at the trie, each node has multiple children. It can have one/two/three or any number of children. Each of the node can store one/two/three or any number of characters (Any node in trie can store non-repetitive multiple characters) Also, every node stores reference to the next node. And finally, the last property is every node keeps a track of end of string. We have empty nodes shown here, I have signed them with black dots. The dots represents that this is the end of the string (this is Boolean value). If the parent of these nodes is the end of the string, we set these nodes' end of string property to true.
Now look at the string, we have multiple strings over here - AIR, AIT, BAR, BIL, BM.
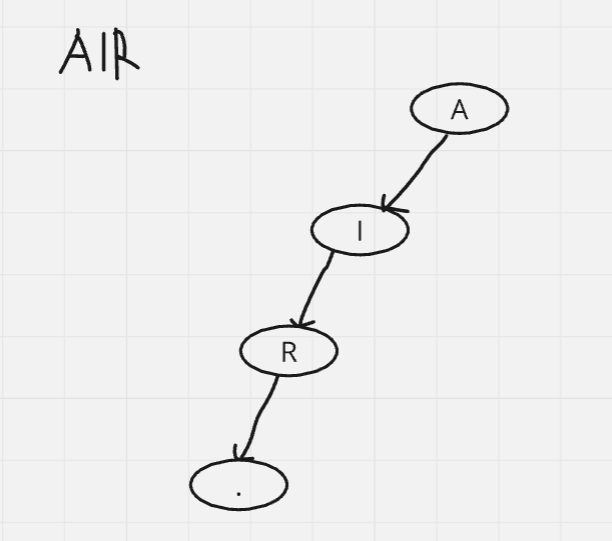
For example, if we want to store AIR, first we have to create a node that stores A, then I, then, R and finally to mention end of the string we have to link a blank node.
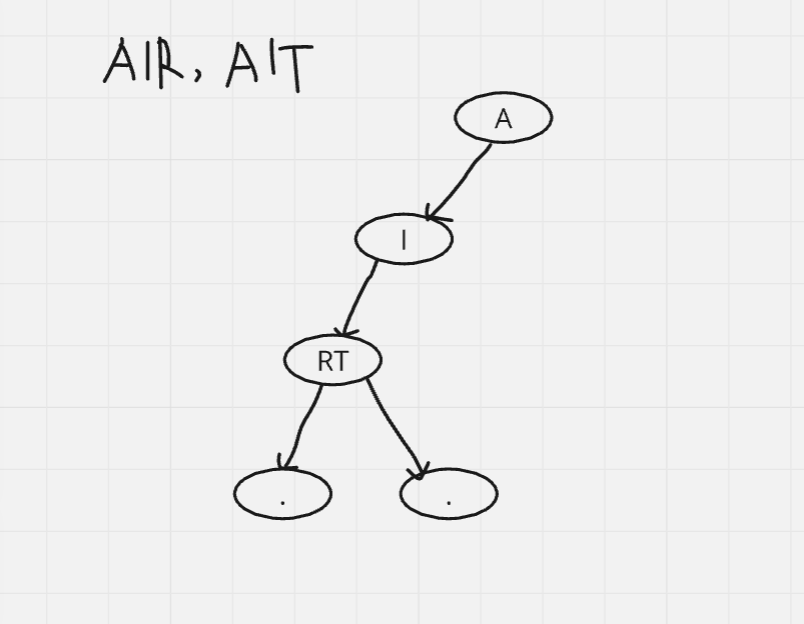
Then, if we want to store another string, we have to create nodes but before that, if any character of the new string exists, then we continue from the next node. We will only add character when there are no existing node for the particular character.
Another string - BAR. After comparing the first character with the root node, we see they are different. So, we insert B into the root node. For the next character, we create a new node and assign the 2nd character to it. Then, another node for R. Finally, a blank node.
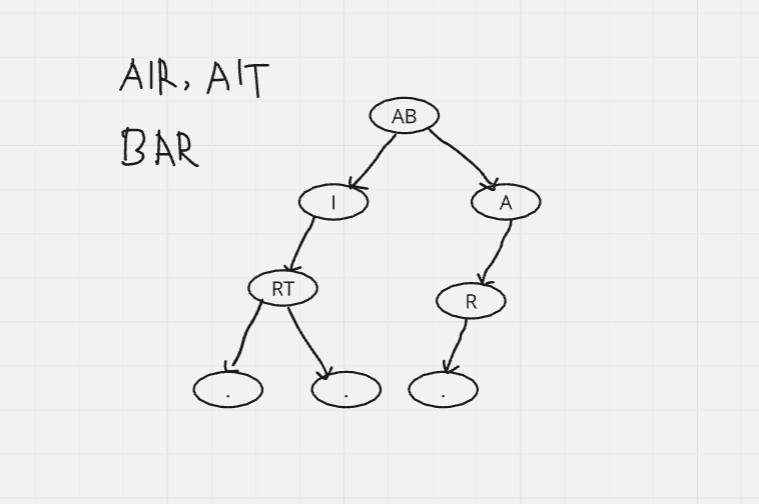
Next - BIL
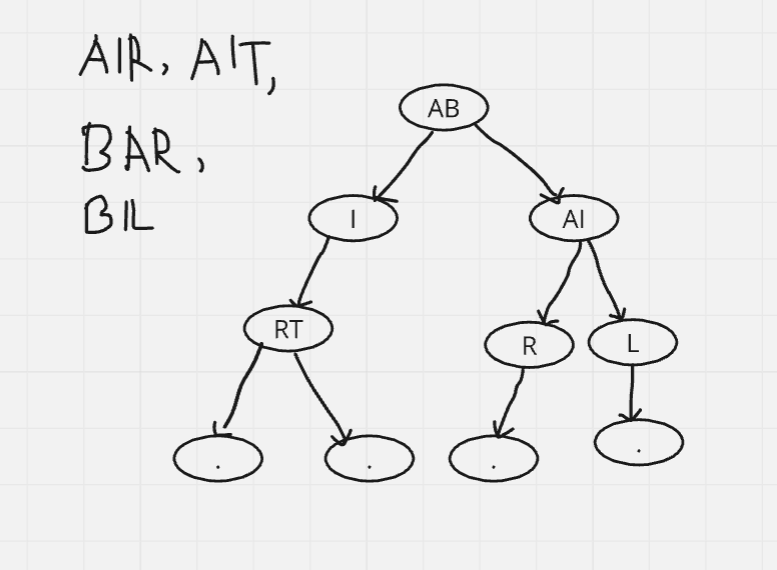
Finally - BM
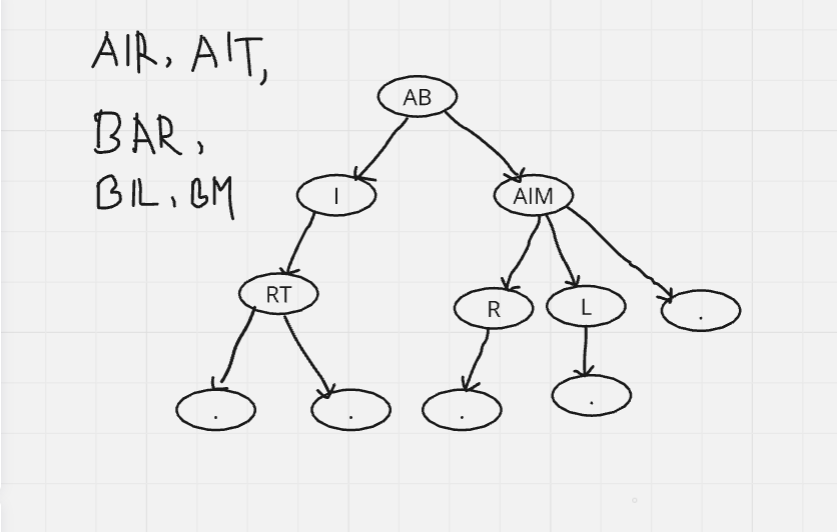
Why we need it?
To solve many standard problems in efficient way
Spelling checker
Auto completion ( google search bar recommendation)
Common operations
The operations are - creating, inserting, searching, deleting.

Based on this logic, we'll create a trie class now
class TrieNode:
def __init__(self):
self.children = {}
self.endOfString = False
class Trie:
def __init__(self):
self.root = TrieNode()
newTrie = Trie()
Time complexity: O(1), Space complexity: O(1)
Insert a string in Trie
There are four cases for insertion:
A Trie is blank
New string's prefix is common to another string prefix
New string's prefix is already present as complete string
String to be inserted is already present in Trie
class TrieNode:
def __init__(self):
self.children = {}
self.endOfString = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insertString(self,word):
current = self.root
for i in word:
ch = i
node = current.children.get(ch)
if node == None:
node = TrieNode()
current.children.update({ch:node})
current = none
current.endOfString = True
print('Successfully inserted')
newTrie = Trie()
newTrie.insertString("App")
newTrie.insertString("Apple")
Time complexity: O(m), Space complexity: O(m). Here, m is the length of the word we want to insert into the trie. We loop through the word and check each character to see if it exists.
Search for a string in Trie
Case 1: String does not exist in Trie
Case 2: String exists in the Trie
Case 3: String is a prefix of another string, but it does not exist in a Trie.
class TrieNode:
def __init__(self):
self.children = {}
self.endOfString = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insertString(self,word):
current = self.root
for i in word:
ch = i
node = current.children.get(ch)
if node == None:
node = TrieNode()
current.children.update({ch:node})
current = none
current.endOfString = True
print('Successfully inserted')
def searchString(self, word):
currentNode = self.root
for i in word:
node = currentNode.children.get(i)
if node == None:
return False
currentNode = node
if currentNode.endOfString == True:
return True
else:
return False
newTrie = Trie()
newTrie.insertString("App")
newTrie.insertString("Apple")
print(newTrie.searchString("Apple")
print(newTrie.searchString("Ape")
print(newTrie.searchString("BBC")
Time complexity: O(m), Space complexity: O(1)
Delete a string from Trie
Case 1: Some other prefix of string is same as the one that we want to delete (AP, APPLE)
Case 2: The string is a prefix of another string (API, APIS)
Case 3: Other string is a prefix of this string (APIS, AP)
Case 4: Not any node depends on this String (K)
class TrieNode:
def __init__(self):
self.children = {}
self.endOfString = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insertString(self,word):
current = self.root
for i in word:
ch = i
node = current.children.get(ch)
if node == None:
node = TrieNode()
current.children.update({ch:node})
current = none
current.endOfString = True
print('Successfully inserted')
def searchString(self, word):
currentNode = self.root
for i in word:
node = currentNode.children.get(i)
if node == None:
return False
currentNode = node
if currentNode.endOfString == True:
return True
else:
return False
def deleteString(root, word, index):
ch = word[index]
currentNode = root.children.get(ch)
canThisNodeBeDeleted = False
if len(currentNode.children) > 1:
deleteString(currentNode, word, index+1)
return False
if index = len(word) - 1:
if len(currentNode.children) >= 1:
currentNode.endOfString = False
return False
else:
root.children.pop(ch)
return True
if currentNode.endOfString == True :
deleteString(currentNode, word, index+1)
return False
canThisNodeBeDeleted = deleteString(currentNode, word, index+1)
if canThisNodeBeDeleted == True:
root.children.pop(ch)
return True
else:
return False
newTrie = Trie()
newTrie.insertString("App")
print(newTrie.searchString("Ape")
deleteString(newTrie, "App", 0)
print(newTrie.insertString("App"))
print(newTrie.searchString("BBC")
End
Subscribe to my newsletter
Read articles from Fatima Jannet directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
