This is the second part of a series of blog posts taking a deep look into the computer program Ada Lovelace developed and published in 1843, starting with Part 1: First Look at the First Program.

OK, in the previous post, I did a quick walk-through of a simplified version, to give a taste of Ada Lovelace’s program from Note G. The whole table is a bit much to take in, but it starts to make sense after stripping away extraneous information.

Questions

Several questions then arise. What is Note G? What are Bernoulli numbers? Why was Ada Lovelace writing a program in 1843 to calculate them? And what specifically is the math she directly implemented in her program?

I’ll now take a step back from trying to get this program running to answer these questions.

Babbage and the Analytical Engine

At the age of 17, Lovelace met Charles Babbage and became fascinated with the possibilities of the Analytical Engine that he was in the process of designing. This would have been the first computer, fully mechanical and driven by steam, and with extraordinary capabilities. Its storage was planned to support 40-digit fixed point numbers or more, and as many as 1000 of them. Babbage predicted it could perform one multiply every minute.¹

Ada Lovelace’s “Notes”

A few years later, after a pause in her studies and after Ada and her husband had their third child, Ada was ready to get back to work on her scientific efforts. In 1842, at age 26, she started translating an article by L.F. Menabrea on the Analytical Engine. Charles Babbage had given a talk in Turin, and Menabrea was so impressed that he published a full account in French.

At the time, women were restricted from scientific publications, but it was considered acceptable for Lovelace to publish an English translation of a man’s work. She set to work translating Menabrea’s article for publishing in English.

As a bit of subterfuge, Lovelace added a series of “Notes” to the translation, signed with just her initials. These “Notes” dwarfed Menabrea’s translated text both in length and in scope. Menabrea’s text was about the Analytical Engine hardware, with almost nothing about the process of writing software, and even seemed to suggest it would be a trivial matter once the math had been worked out.

Lovelace’s “Notes”, on the other hand, are more than twice as long as Menabrea’s text and are almost entirely about software. She discussed how to develop it and how to analyze its performance, and she gave a vision of the possibilities of software and a new “science of operations.” She ended these Notes with “Note G”, an extended example and analysis of the first non-trivial program, her program capable of “computing the [Bernoulli] Numbers to an indefinite extent, from the very beginning.”²

Lovelace chose this “rather complicated example” of computing Bernoulli numbers because it was a fresh topic being discussed by mathematicians of the day. Showing that such a complicated calculation could be carried out automatically, and accurately, by a steam-powered machine would concretely show the value of the Analytical Engine.

In the previous post, I walked through a bit of the math in Lovelace's program. You can follow along as the basic arithmetic operations combine values to construct the algebraic results listed in the comments. If you’re going to run it, though, you need to know a bit more about the underlying math. As we’ll find out, some debugging will be necessary, and that’s not really possible without a more solid understanding.

So what are Bernoulli numbers?

The Numbers of Bernoulli

In the early 1700s, Swiss mathematician Jakob Bernoulli discovered a series of numbers that made it easier to calculate sums of powers of the form 1^k+2^k+3^k+...+n^k.

For example, if k=1 then, 1¹+2¹+3¹+...+n¹ = n(n+1)/2. This is just simply summing the numbers from 1 to n.

With k=2, you have 1²+2²+3²+...+n² = [n(n+1)(2n+1)] / 6, and the calculations get progressively more complicated from there.

Bernoulli had an insight that speeds up the calculations using special polynomials with coefficients that became known as the Bernoulli Numbers. Some progress had been made on this problem by the early 18th century, but Bernoulli (and also Seki Takakazu, independently) had an insight that known formulas for the sums could be refactored slightly, giving a striking pattern in the aligned columns:

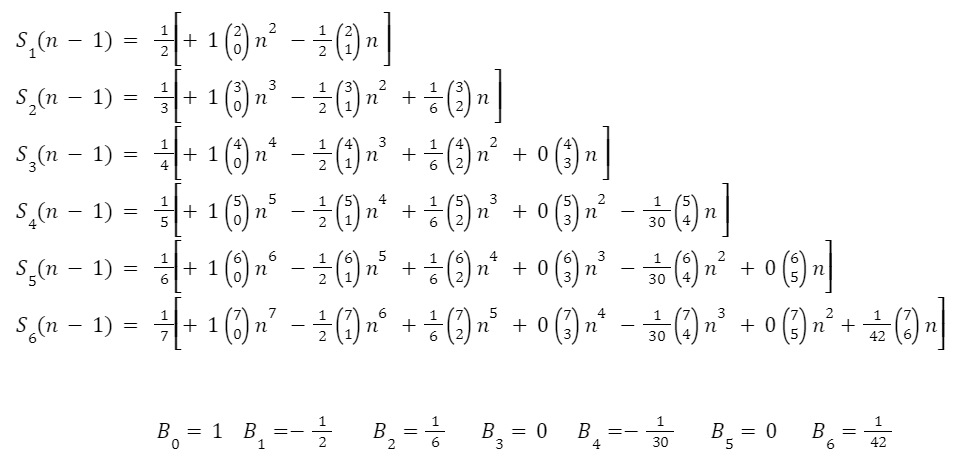
Arranging the sum formulas in this way, you can see terms lining up in columns within the square brackets. Each term has three parts. The first part is the coefficient that collectively became known as Bernoulli Numbers. Next is just the easily calculated combinatorial for Pascal's triangle. The last is simply n raised to a power.

You can see that for any power, the Bernoulli Numbers are the same, so they only need to be calculated once. In the above table, the B₀ through B₆ sequence can be seen.

As an example, we can verify that S₃(9) would be:

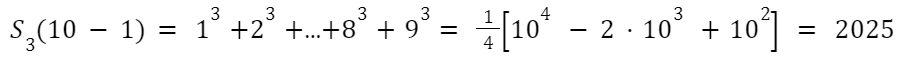
Mathematicians have since found that this series of numbers has a deep connection to other long-running questions in mathematics "including the series expansions of trigonometric and hyperbolic trigonometric functions, the Euler-Maclaurin Summation Formula, the evaluation of the Riemann zeta function, and Fermat’s Last Theorem."³

Calculating Bernoulli Numbers

These Bernoulli numbers, though, weren’t trivial to calculate. Lovelace lists in Note G a few different formulas that could be used to calculate them, along with the one formula she actually implemented.

Before his death, Bernoulli had calculated up to B₁₀ in the 1680s, continuing from B₀ through B₆ above with:

B₇ = 0, B₈ = -1/30, B₉ = 0, B₁₀ = 5/66.

By 1748, Euler had extended these calculations to B₃₀. Martin Ohm published the efforts of a professor Rothe, who extended this to B₅₀ in 1817 and B₆₂ in 1840. This was just a couple years before Lovelace began work on her Notes and her program, suggesting she likely would have been aware of the development. Interestingly, Rothe also called attention to an error in one of Euler’s published numbers.⁴

Fortunately for us, you can now find precise Bernoulli numbers on WolframAlpha or in the free online book, The First 498 Bernoulli Numbers by Simon Plouffe.

How far might Lovelace have hoped to calculate?

In an 1843 letter to Babbage she was clear in her goal of giving "an example of how an implicit function may be worked out by the engine, without having been worked out by human head & hands first."⁵

The minor historical detail, not mentioned in her Notes, that Bernoulli numbers to B₆₂ had recently been calculated suggests that Lovelace’s ambition for the program’s “indefinite extent” was to B₆₄ and beyond. Still without the help of computers, decades later, J.C. Adams pushed the record further to B₁₂₄.⁶ One interesting question I will investigate is how would Lovelace’s program have compared to these efforts had the Analytical Engine been built before Charles Babbage’s death in 1871?

Be aware that before there was consensus on a convention for numbering Bernoulli numbers, there were a few different conventions. Importantly, Lovelace's numbering convention is offset by one from the accepted modern numbering.

Her “B₁, B₃”… numbering is just the equivalent of modern B₂, B₄... When debugging Lovelace’s program, it is handy to have a table nearby with full high-precision decimal expansion, numbered using her convention. Likewise, the B₆₂ previously published, would have been B₆₁ by Lovelace's numbering convention.

Altogether, her goals for the program could be stated as:

"Compute the [Bernoulli] Numbers"
"to an indefinite extent": iterating to calculate B_n, B_n+1, etc. until you choose to halt the machine.
"from the very beginning": starting with B₁.
"without having been worked out by human head & hands first": to at least B₆₃.

This would be at a minimum, computing B₁,B₃,B₅,...,B₆₃ by her numbering convention.

With that clarified, we can take a look at the math she implemented in her program.

The Algebraic Formulæ

The bulk of Note G, after some more general discussion, appears similar to explanations one might find in modern block comments above a section of source code. She starts with “We will terminate these Notes by following up in detail the steps through which the engine could compute the Numbers of Bernoulli, this being (in the form in which we shall deduce it) a rather complicated example of its powers.” Then she moves on to the math she will be using.

First, she gives algebraic equations 1-3 for Bernoulli numbers as alternate examples of ways to generate the numbers. These formulas are not used in the program. Next she gives the algebraic derivation, equations (4.)-(9.), of a preferred generating function for Bernoulli numbers. Equations (8.) and (9.) are the important ones for understanding the code as these are what she implemented directly:

(8.) 0 = -1/2*(2n-1)/(2n+1) + B₁*(2n/2) + B₃*(2n*(2n-1)*(2n-2)/(2*3*4)) + B₅*(2n*(2n-1)...(2n-4)/(2*3*4*5*6)) + ... + B_2n-1

which it may be convenient to write under the general form:

(9.) 0 = A₀ + A₁B₁ + A₃B₃ + A₅B₅ + ... + B_2n-1

If you look at the table, in comments in the “Statement of Results” column, you can see the definitions of A₀, A₁, A₃ as functions of n:

-1/2*(2n-1)/(2n+1) = A₀

2n/2 = A₁

2n/2 (2n-1)/3 (2n-2)/4 = A₃

The trick to this math is that even though (9.) goes on infinitely with … A₇B₇ + A₉B₉ + A₁₁B₁₁ + … and so on, for any given n, the A_2n-1 term at the point we care about becomes one, and every A term after that becomes zero. This is the trick that lets you calculate a Bernoulli number knowing only the preceding ones. I encourage you to try out different values of n starting at one to convince yourself this works. Lovelace points this out in the text:

whatever n is, every term of (8.) after the (n+1)th is =0, and that the (n+1)th term itself is always =B_2n-1*1/1 = B_2n-1, enables us to find the value (either numerical or algebraical) of any nth Number of Bernoulli B_2n-1, in terms of all the preceding ones, if we but know the values of B₁, B₃…B_2n-3.

An important point for the program is that these A terms aren’t constant but rather functions of n. This is why the program can’t just store them once but has to recalculate them for every n. Maybe an easier way to picture (9.) would be (note the negation):

B_2n-1 = -(A₀(n) + A₁(n)B₁ + A₃(n)B₃ + A₅(n)B₅ + … )

These algebraic equations and derivation in Note G are most likely what Babbage referred to years later as the “algebraic working out” of the Bernoulli numbers that he gave to Lovelace and that she corrected:

the selection was entirely her own. So also was the algebraic working out of the different problems, except, indeed, that relating to the numbers of Bernoulli, which I had offered to do to save Lady Lovelace the trouble. This she sent back to me for an amendment, having detected a grave mistake which I had made in the process.

The Algorithm

With the math understood she now lays out the iterative strategy for “computing the Numbers to an indefinite extent, from the very beginning.” This is the algorithm that she then developed as a starting point for writing the program in the table:

On attentively considering (8.), we shall likewise perceive that we may derive from it the numerical value of every Number of Bernoulli in succession, from the very beginning, ad infinitum, by the following series of computations:—

1st Series.—Let n=1, and calculate (8.) for this value of n. The result is B₁.
2nd Series.—Let n=2. Calculate (8.) for this value of n, substituting the value of B₁ just obtained. The result is B₃.
3rd Series.—Let n=3. Calculate (8.) for this value of n, substituting the values of B₁, B₃ before obtained. The result is B₅. And so on, to any extent.

Lovelace's Process of Programming

In addition to the example program, Lovelace wrote extensively about the process of programming. The lessons spread throughout the notes, either directly shown for her example or given as more general commentary, show the methodical process she actually used:

Derive needed mathematical formulæ, such as formula (8.) for the nth Bernoulli number given previous Bernoulli numbers. [Note G, near end]
Develop the “nth function” as a way of determining “cycles” which can be nested arbitrarily deep. This bridges the gap between the abstractness of the underlying math and the concrete operations needed to implement it. [Note E]
Define variables and their purpose "into three classes": input “Variables for data”, “Result-Variables” for final results, and “Working-Variables” for transient use between. [Note D]
Arrange the processes and allocate variables so that “the offices performed by the Variables may be as uniform and fixed as possible.” [Note G, near end]
Optimize runtime performance by choosing “that arrangement which shall tend to reduce to a minimum the time necessary for completing the calculation.” [Note D, end]

Once you get past the archaic language used, it sounds at least a bit familiar to anyone who has written a lot of code.

Now… Let’s Run it

OK, with a bit more understanding of the math, it’s time to try to run this code and see what happens.

The next post will look at what it means to "run" a program, in preparation for a first stab at running Lovelace's program.

Passages from the Life of a Philosopher, by Charles Babbage (1864). "One multiplication of two numbers, each of fifty figures, in one minute."
"Sketch of the Analytical Engine invented by Charles Babbage, By L. F. Menabrea of Turin, Officer of the Military Engineers." Translation originally published in 1843 in the Scientific Memoirs, 3, 666-731. Lovelace's translation included the extensive Notes A-G including the table program for calculating Bernoulli Numbers.
Peter Larson. “The Bernoulli Numbers: A Brief Primer”. (2019).
“Etwas über die Bernoullischen Zahlen.” - Martin Ohm, 1840. "The first 15 of them can be found in Euler's Instit. Calculi diff. P. II. Cap. V. the following 10 were calculated by Professor Rothe in Erlangen and printed in the Allgemeine Litteratur-Zeitung (in Halle) No. 63, March 1817. Finally Rothe also gave me the last 6 (up to 31 inclusive). [...] Finally we would like to take this opportunity to recall a calculation error that occurs in Euler's Instit. Calculi diff. P. II. Cap. VII." This probably refers to Heinrich August Rothe.
Ada, the Enchantress of Numbers: Poetical Science, by Toole, Betty Alexandra (2010)
It’s worth pointing out that before the 20th century, there were multiple different conventions in how to refer to the numbering of Bernoulli numbers. For example, when Adams published what is now called B₁₂₄, he referred to it as “B₆₂” by an older convention that ignores the trivial zeros. Lovelace used yet another convention, closer to the modern convention, but offset by one, so Lovelace's "B₁" would be the equivalent of the modern B₂.

Part 2: Some Background