Topological Sort Algorithm
 Fatima Jannet
Fatima Jannet
Topological sort is crucial in scenarios like task scheduling, resolving symbol dependencies in compilers, and determining build orders in software projects. This is going to be a quick blog on the Topological Sort Algorithms.
Let's start!
Topological Sort
Topological Sort: Sorts given actions in such a way that if there is a dependency of one action on another, then the dependent action always comes later than its parent action.
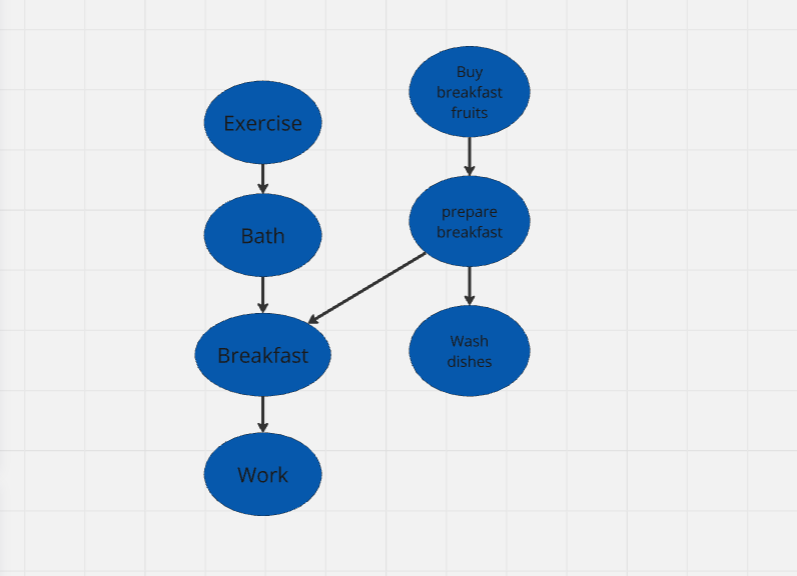
Explanation: With the tasks given, there are also parallel tasks. We need to buy breakfast fruits, prepare breakfast, and wash dishes. We can't have breakfast without preparing it, and we can't prepare it without buying fruits. The "Breakfast" action depends on these tasks. Similarly, we can't have breakfast if we don't take a bath or exercise. The arrows signifies that an action can only be done after the previous one.
In short, the topological order basically helps us to solve the problem of ordering actions that need to be done
Topological Sort Algorithm
If a vertex depends on currentVertex:
Go to that vertex and then come back to currentVertex
Else, push currentVertex to stack.
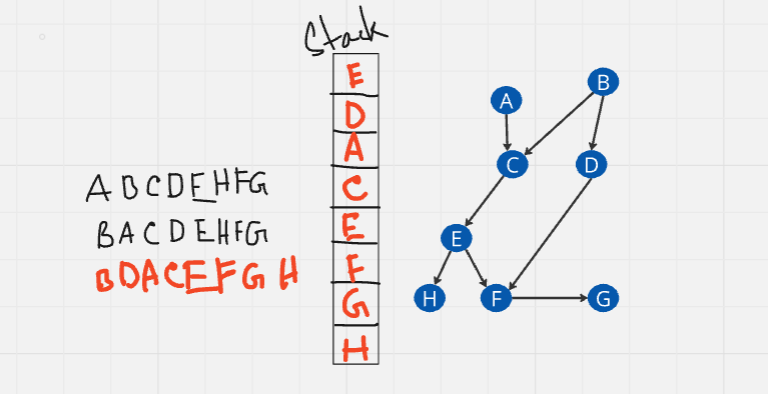
If we start from A, we see that C depends on A. According to the algorithm, we check if a vertex depends on the current vertex. So, C depends on A, and A is the current vertex. After going to C, we see another vertex, E, depends on C. We continue to E, where two nodes depend on E. We move to H, which has no nodes depending on it. According to the else condition, we push H to the stack. Returning to E, we find another node, F, depends on E. Moving to F, we see another node depends on F. We follow the else condition for G, pushing G to the stack.
Topological Sort in Python
from collection import defaultdict:
class Graph:
def __init__(self, numberOfVectices):
self.graph = default(list)
self.numberOfVertices = numberOfVectices
def addEdge(self, vertex, edge):
self.graph[vertex].append(edge)
def topologicalSortUntil(self, v, visited, stack):
visited.append(v) #O(1)
for i in self.graph[v]: #O(E)
for i not in visited:
self.topologicalSortUntil(i, visited, stack)
stack.insert(0, v) #O(1)
def topologicalSort(self):
visited = [] #O(1)
stack = [] #O(1)
for k in list(self.graph): #O(E+V)
if k not in visited:
self.topologicalSortUntil(k, visited, stack)
print(stack)
customGraph = Graph(8)
customGraph.addEdge["A", "C"]
customGraph.addEdge["C", "E"]
customGraph.addEdge["E", "H"]
customGraph.addEdge["E", "F"]
customGraph.addEdge["F", "G"]
customGraph.addEdge["B", "D"]
customGraph.addEdge["B", "C"]
customGraph.addEdge["D", "F"]
customGraph.topologicalSort()
The number of vertices is V, so this loop here will take O(E+V) time complexity. Space time is also O(E+V) because we have created two lists in the code.
Time complexity : O(E+V), Space complexity: O(E+V)
End.
Subscribe to my newsletter
Read articles from Fatima Jannet directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
