Mathematical concept of Euclidean distance similarity metric for vector databases

In Math and Physics vectors play a key role in almost every aspect of the subjects. By definition a vector is an entity that has both magnitude and direction over a given space.

The following schematic shows a representation of a vector in one dimensional space that points from point A to point B and has a magnitude of u along with the vector expression for points (2,3).

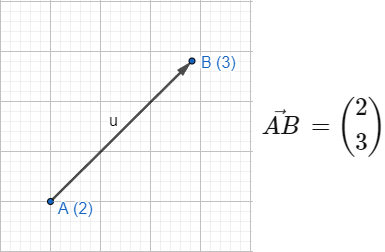
Please note that vectors can span over a single dimension or multiple dimensions.

Vector Embedding

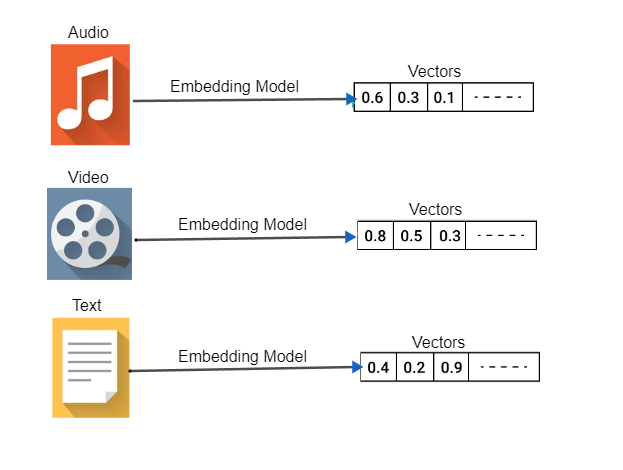
In vector databases, vector embeddings are created by numerical representations of non numerical data. For instance, an image can be represented in form of vector embedding that comprises of its pixel values with each pixel representing a combination of hue, color saturation, contrast and brightness in form of a vectors. Similarly for audio the vector embedding would consist of amplitude, frequency and wavelength presented as vectors.

Similarity search

Similarity search play a key role in understanding of complex unstructured data. At its core similarity methods help understand the fundamental relation across set of vectors. By leveraging similarity between vectors across given objects, we can understand the level of similarity across them. In other words similarity search helps understand the fundamental relation across set of vectors of the objects and identify key patterns. In similarity search more related objects are placed closed to each other.

Similarity Metrics

There are three major similarity metrics that are used to identify and compute similarities across vector embeddings. They are

• Euclidean

• Cosine

• Dot product

In this post we will explore the mathematical foundation of Euclidean similarity metric.

In fundamental math, Euclidean distance computes the distance between two points. Lets say we have two points A and B on a two dimensional space

$$A(x_1,y_1)\hspace{1.5 mm} ,\hspace{1 mm} B(x_2,y_2)$$

and the distance between them is represented as d .

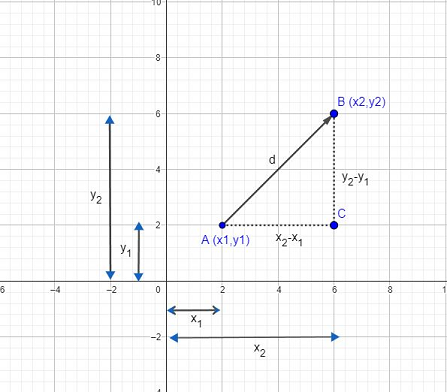
To compute the distance d between the A and B , we would construct right angle triangle which meets at point C. Using Pythagorean theorem for triangle ABC we have

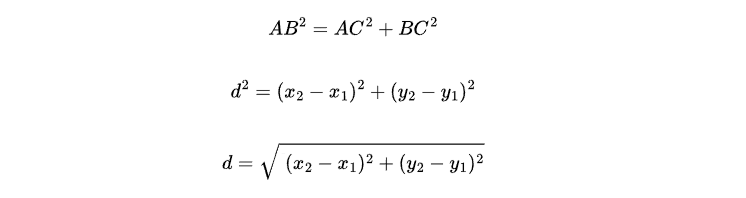
The derived Euclidean formula is :

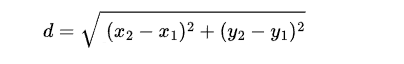
Lets look into an example. Suppose that there are two points A and B on a two dimensional space or a plane

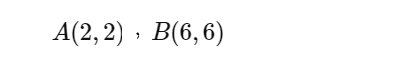
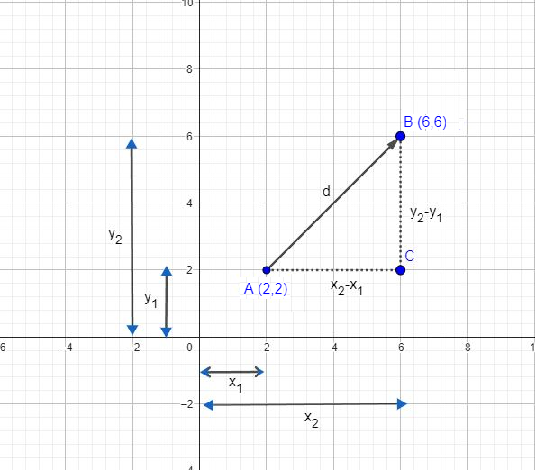
To find distance between the two points, we substitute their values in the formula

$$d=\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\\$$

that we derived earlier.

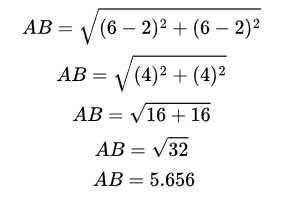
The calculated Euclidean distance between points A and B is 5.656 units

The vector from A to B is calculated to

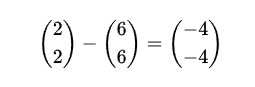
and the length of this vector is the distance between A and B that we computed earlier which is 5.656 units.

Euclidean distance in Two dimensional space is calculated as

$$d=\sqrt{(x_2 - x_1)^2 +(y_2 - y_1)^2}$$

For Three dimensional space Euclidean distance is

$$d= \sqrt{(x_2 - x_1)^2 +(y_2 - y_1)^2 +(z_2 - z_1)^2}$$

For N dimensional space the Euclidean distance is

$$d= \sqrt{{∑_{v=1}^n}(x_{vi} – x_{vj})^2}$$

where points

$$(x_{1i}, x_{2i}, x_{3i}, …., x_{ni}) \text{ and }(x_{1j}, x_{2j}, x_{3j}, …., x_{nj})$$

are in N dimensions.

Enough of theory. Lets get to the practical stuff.

Let us now write a simple python program to compute the Euclidean distance across point A and point B in two dimensional space for the same value points that we used earlier.

import numpy as np

#numpy arrays
v1 = np.array((2,2))
v2 = np.array((6,6))

#difference between 2 vectors
V = v1 - v2

#calculating Euclidian distance
euclid_distance = np.sqrt(np.dot(V.T, V))

#printing the output
print(euclid_distance)

The output that we get is 5.6568... which is exactly same to what we got when we manually computed the equation.

We can rewrite the above code by leveraging SciPi library and use the inbuilt Euclidean distance formula function

import numpy as np

# import scipi
from scipy.spatial import distance

#numpy arrays
v1 = np.array((2,2))
v2 = np.array((6,6))

# Calculate Euclidean distances across two vectors
distances = distance.euclidean(v1,v2)

print(distances)

It outputs the exact same value : 5.6568...

Now that we understand the basic fundamental foundation of Euclidean distance metric, lets see how can we use it in similarity search. In essence, if the Euclidean distance across given vectors are 0 it would mean they are exactly the same and more further the value moves away from 0 the similarity is more distant across them.

For example if we would like to do a similarity search between "car" and "car", the vector representation would be the exact same and the Euclidean distance will be 0.
But if we perform a similarity search between "car" and "elephant" the vector representation would be quite different and Euclidean distance computed would be distant apart compared to "car" and "car".

Lets implement a real life example of Euclidean distance similarity search with Python. In the following example we would perform similarity search by computing the Euclidean distance across 3 phrases and see how closely they are related to each other.

• 'Paris is capital of France'

• 'Boeing and Airbus are two companies that build aircrafts'

• 'Rome is capital of Italy'

import numpy as np
from scipy.spatial import distance
from sklearn.metrics.pairwise import euclidean_distances


corpus = [ 'Paris is capital of France',
           'Boeing and Airbus are two companies that build aircrafts',
           'Rome is capital of Italy'  ]

from sklearn.feature_extraction.text import CountVectorizer

V = CountVectorizer().fit_transform(corpus).toarray()

v1=(V[0, :] )
v2=(V[1, :] )
v3=(V[2, :] )

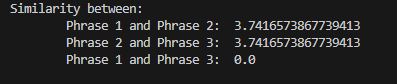
print('Similarity between: ')
print('\tPhrase 1 and Phrase 2: ', distance.euclidean(v1,v2))
print('\tPhrase 2 and Phrase 3: ', distance.euclidean(v2,v3))
print('\tPhrase 1 and Phrase 3: ', distance.euclidean(v1,v3))

and we get the following output.

As expected the similarity value between Phrase1 and Phrase3 was the minimum compared to the other comparisons.

If we copy Phrase1 to Phrase3 we get the similarity value of 0 which is quite obvious as the two phrases are exactly the same.

Closing Notes

In this article we looked into the fundamental mathematical building block of Euclidean distance that forms a back bone of the similarity search algorithm in vector databases. Also we practically looked into how to implement it through Python libraries.