Đường cong Bézier

Đây là bài viết cung cấp các kiến thức cơ sở nền tảng để hiểu series bài viết về khớp đường cong cho tập điểm.

Chắc hẳn gần như ai đã từng dùng các ứng dụng vẽ hình, thiết kế đồ họa đều đã sử dụng qua công cụ vẽ đường cong dạng thế này:

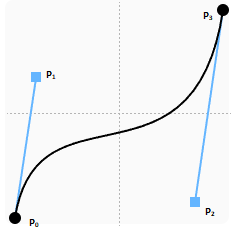
Một đường cong như trên được gọi là một đường cong Bezier bậc ba, bao gồm 4 control points: hai điểm (hình tròn đen) ở đầu mút và hai điểm điều chỉnh độ uốn (hình vuông xanh). Để cho tiện, ta đặt tên cho 4 điểm này lần lượt là \(P_0,P_1,P_2,P_3\), ta có phương trình để vẽ đường cong bậc 3 được định nghĩa như sau:

\(\textbf{B}(t)=(1-t^3)P_0+3(1-t)^2P_1+3(1-t)t^2P_2+t^3P_3, \quad 1 \ge t \ge 0\)

Mình xin phép không đi quá sâu vào lý do tại sao có công thức trên, bạn đọc hoàn toàn có thể tìm thấy nguồn giải thích dễ dàng trên các trang khác.

Ở đây, các điểm \(P_0,P_1,P_2,P_3\) được coi như các vector trên mặt phẳng 2 chiều có tọa độ \((x,y)\). Phép nhân các điểm này với một số thực được coi như một phép scale:

\(tP(x,y) = (x\times t, y \times t)\)

Từ công thức tính \(\textbf{B}(t)\)ở trên, ta có thể vẽ đường cong Bezier bằng cách:

• Chia đoạn \([0,1]\)ra thành \(n\) phần bằng nhau \(t_0=0, t_1=1/n,t_2=2/n,\dots, t_n=1\)

• Tính các giá trị \(\textbf{B}(t_i), i\in\{0,1,\dots,n\}\) để tìm ra một tập hợp điểm nằm trên đường cong: \(\{(x_0,y_0),(x_1,y_1),\dots,(x_n,y_n)\}\)

• Vẽ các đường thẳng nối các điểm này lại với nhau

Source code Javascript sử dụng P5JS

var Bezier = function(p1, p2, p3, p4){
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
    this.p4 = p4;

    // chia đường cong thành n đoạn thẳng nhỏ
    // bằng cách tính tọa độ các điểm trên trên đường cong
    // rồi nối toàn bộ lại với nhau
    // nSegs là số đoạn cần chia
    this.segmentation = function(nSegs){
        let inc = 1.0 / nSegs; // increment step
        let t = 0;
        let arr = [];

        for (let i = 0; i < nSegs; i++){
            // các tham số, xem lại công thức tính B(t)
            let t1 = 1 - t;
            let t1_3 = t1*t1*t1;
            let t1_3a = (3*t)*t1*t1;
            let t1_3b = (3*t*t)*t1
            let t1_3c = t*t*t;

            // tính tọa độ x
            let x = t1_3 * this.p1.x
            x = x + t1_3a * this.p2.x;
            x = x + t1_3b * this.p3.x;
            x = x + t1_3c * this.p4.x
            // tính tọa độ y
            let y = t1_3  * this.p1.y;
            y = y + t1_3a * this.p2.y;
            y = y + t1_3b * this.p3.y;
            y = y + t1_3c * this.p4.y;

            // lưu tọa độ vào mảng
            arr.push({"x":x, "y":y});            
            t = t + inc;
        }

        return arr;
    }

    this.draw = function(){
        // chia đường cong thành nhiều đoạn rồi        
        // tính tọa độ các điểm trên đường cong
        let segments = this.segmentation();

        // vẽ các đường thẳng nối các điểm lại với nhau
        for (let i = 0; i < segments.length - 1; i++){
            line(segments[i].x, segments[i].y, segments[i+1].x, segments[i+1].y);
        }
    }
}