Data Representation and Overflow
 Ahmed Gouda
Ahmed GoudaComputers store data as a sequence of binary bits.
Bit, Byte, Halfword, Word, and Double-word
A Bit is the smallest quantity of information. Each bit has a value of either one or zero, and thus it is called a binary bit. However, it is more efficient for computers to load, process, store, and transmit a group of bits simultaneously. Therefore, bits are divided into a sequence of fixed-length logic units.
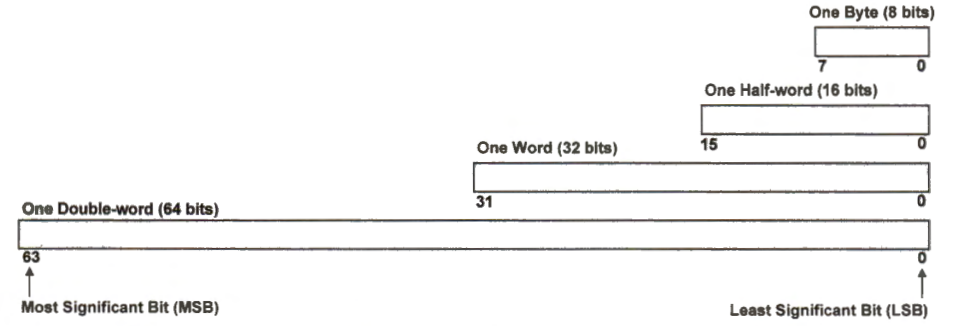
As shown in the below figure,
Byte is a group of 8 bits
Half-word consists of 16 bits (or 2 bytes)
Word has 32 bits (or 4 bytes)
Double-word contains 64 bits (or 8 bytes).
The most significant bit (MSB) and the least significant bit (LSB) of a byte are the bit at the leftmost and rightmost position, respectively. However, MSB and LSB may be located at some other positions in these units (big endian and little endian).
The C standard specifies the minimum size of basic data types. The actual size of a variable relies on the implementation of C compilers. Below Table gives the typical size of some data bytes. A pointer in a C program is a special variable that holds the memory address of a variable stored in memory. On 32-bit processors, a pointer has 32 bits. Each register in Cortex-M processors has 32 bits. Accordingly, a register can hold a pointer or all basic data types listed except double. A double variable takes two registers.
| Basic data type of C language | Typical size in memory |
| char | 1 byte |
| short | 2 bytes or 1 halfword |
| signed/unsigned integer | 4 bytes or 1 word |
| signed/unsigned long | 4 bytes or 1 word |
| signed/unsigned long long | 8 bytes or 1 double word |
| float | 4 bytes or 1 word |
| double | 8 bytes or 1 double word |
A byte is the smallest unit that can be transferred into or out of memory. Each byte in memory has a memory address.
A halfword, word, and double-word span 2, 4, and 8 consecutive bytes in memory, respectively.
By convention, if a variable takes multiple bytes in memory, the processor uses the lowest memory address of these bytes as the memory address of this variable. For example, if a C integer variable takes four bytes in memory (0x20000000 - 0x20000003), the memory address of this integer variable is 0x20000000.
In general, to modify a bit in memory, a processor should load at least a byte from memory and then operate on the target bit. ARM Cortex-M processors provide a performance-enhancement technique called bit banding, which allows the processor to store or modify a bit directly.
Binary, Octal, Decimal, and Hexadecimal Numbers
We can represent an integer with different base values. Four commonly used bases are binary (base 2), octal (base 8), decimal (base 10), and hexadecimal (base 16). In general, an n-digit integer N in the base b has the following form:
$$a_{n-1}a_{n-2}a_{n-3}...a_{1}a_{0}$$
We can calculate its equivalent decimal value N as follows:
$$N = a_{n-1}*b^{n-1}+a_{n-2}*b^{n-2}+a_{n-3}*b^{n-3}+ ... +a_{1}*b+a_{0}$$
For example, in the decimal system (base 10), the number 201410 means
$$2014_{10}=210^{3}+010^{2}+1*10^{1}+4$$
Similarly, in the octal system (base 8), the number 13758 represents
$$1375_{8}=18^{3}+38^{2}+7*8^{1}+5=765_{10}$$
The below table shows the conversion of a decimal number between 0 and 15 to its equivalent in decimal, binary, octal, and hexadecimal (hex for short). Because binary numbers are verbose, programmers often use hex numbers in programs.
We can convert a binary number to its hex equivalent by separating binary bits into groups of four and replace each group of four binary digits with its equivalent hex digit.
| Decimal | Binary | Octal | Hex |
| 0 | 0000 | 00 | 0x0 |
| 1 | 0001 | 01 | 0x1 |
| 2 | 0010 | 02 | 0x2 |
| 3 | 0011 | 03 | 0x3 |
| 4 | 0100 | 04 | 0x4 |
| 5 | 0101 | 05 | 0x5 |
| 6 | 0110 | 06 | 0x6 |
| 7 | 0111 | 07 | 0x7 |
| 8 | 1000 | 010 | 0x8 |
| 9 | 1001 | 011 | 0x9 |
| 10 | 1010 | 012 | 0xA |
| 11 | 1011 | 013 | 0xB |
| 12 | 1100 | 014 | 0xC |
| 13 | 1101 | 015 | 0xD |
| 14 | 1110 | 016 | 0xE |
| 15 | 1111 | 017 | 0xF |
In C, the prefix "0" represents octal, and the prefix "0x" or "0X" represents hexadecimal. The following gives examples of defining constant numbers in C. Some C compilers do not support directly declaring a binary number.
int k;
k = 0xA; // hex constant, k = 10 in decimal
k = 0XA; // 0X is the same as 0x
k = -0xA; // hex constant, k = -10 in decimal
k = 012; // octal constant, k = 10 in decimal
; = 0b1010; // binary constant, k = 10
Unsigned Integers
How many unique symbols can n binary bits represent? Because each bit has two possible values, either one or zero, n bits can represent a total of 2^n different symbols.
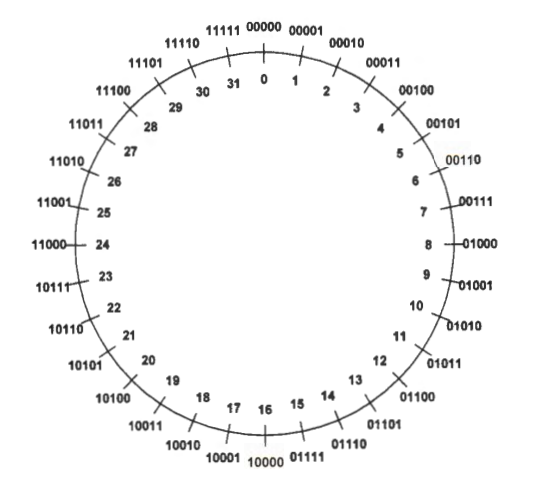
For example, with 5 bits, we can have 2^5 (i.e., 32) symbols, including 0b00000, 0b00001, 0b00010, ..., and 0b11111. To use these symbols to represent numbers, we need to establish a mapping between each symbol and the number it represents.
Let us first look at unsigned numbers. Since each unsigned number can be represented in binary, it is natural for computers to store them using their binary representation directly. The below figure shows the mapping between unsigned numbers and all binary symbols in a five-bit system. If a n-bit string represents an unsigned number, the representable range is 0, 2^n - 1, including zero and 2^n - 1 positive integers.
Signed Integers
There are different ways to map binary symbols to signed integer numbers. Examples include:
Sign-and-Magnitude
uses the most significant bit to represent the sign and the rest of the bits to represent the magnitude.One's Complement
denotes a negative number by inverting every bit of its positive equivalent.Two's Complement
represents a negative number by adding one to the equivalent one's complement.
One common characteristic of these numeral systems is that the most significant bit (also called the leftmost bit) indicates the sign of the number. This bit is also known as the sign bit. The number is non-negative if the sign bit is zero and negative if it is one.
| Binary Bit String | Sign-and-Magnitude | One's Complement | Two's Complement | |
| 0000 | +0 | +0 | 0 | |
| 0001 | 1 | 1 | 1 | |
| 0010 | 2 | 2 | 2 | |
| 0011 | 3 | 3 | 3 | |
| 0100 | 4 | 4 | 4 | |
| 0101 | 5 | 5 | 5 | |
| 0110 | 6 | 6 | 6 | |
| 0111 | 7 | 7 | 7 | |
| 1000 | -0 | -0 | -8 | |
| 1001 | -1 | -1 | -7 | |
| 1010 | -2 | -2 | -6 | |
| 1011 | -3 | -3 | -5 | |
| 1100 | -4 | -4 | -4 | |
| 1101 | -5 | -5 | -3 | |
| 1110 | -6 | -6 | -2 | |
| 1111 | -7 | -7 | -1 |
If the bit string has n bits. The range means the largest and the smallest values that these bit strings can represent.
| Sign-and-Magnitude | One's Complement | Two's Complement | |
| Range | -2^n-1 + 1 : 2^n-1 - 1 | -2^n-1 + 1 : 2^n-1 - 1 | -2^n-1 , 2^n-1 - 1 |
| Zero | Two zeros (+0, -0) | Two zeros (+0, -0) | One zero |
| Unique Numbers | 2^n-1 | 2^n-1 | 2^n |
In C, the range that a signed integer variable can represent depends on its data type. An integer variable of "signed char," "signed short," "signed int," and "signed long long" has at least 8, 16, 32, and 64 bits in size, respectively. The C standard only specifies the minimum size of integer types, and their actual size varies by implementation.
Two's complement is the one used in almost all modern computers to represent signed integers because it simplifies the hardware design from two aspects:
The hardware for two's complement subtraction is the same as that for two's complement addition.
The hardware implementations for adding, subtracting, and multiplying signed numbers are identical to those for unsigned numbers.
Sign-and-Magnitude
$$value = (-1)^{sign} * Magnitude$$
Sign-and-Magnitude is a straightforward way to represent signed integers. It uses the most significant bit to indicate the sign, with one being negative and zero being positive. The remaining n-1 bits represent the value.
For example, in a five-bit system, 0b10111 is -7, and 0b00111 is 7.
There are two ways to represent zero: 0b00000 for +0 and 0b10000 for -0.
Many computer systems do not use the sign-and-magnitude due to two shortcomings.
First, it is difficult for the hardware to perform addition or subtraction because the hardware should consider the sign of both operands. If we add two numbers in a straightforward way, such as
00011(3) + 11011 (-3), we get a wrong answer,11110 (-14).Second, there are two representations of zero: positive zero and negative zero. A system with two zeros complicates the circuit for checking for equality.
One's Complement
$$\tilde{\alpha} = 2^{n} - 1 - \alpha$$
$$\alpha + \tilde{\alpha} = 2^{n} - 1$$
The one's complement representation of a negative number is bitwise NOT of its positive counterpart. For example, in a five-bit system, the one's complement of -1 is 0b11110.
The word "complement" means that two counterparts complete the whole.
Specifically, the one's complement and its counterpart add to 2^n - 1. For example, adding 0b00001(+1) and 0b11110 (-1) leads to 0b11111, which is in fact negative zero.
A simple way to find the one's complement is to toggle every bit in its counterpart. In C, the bitwise NOT operator (~) is also called the one's complement operator.
y = ~y; // Take one's complement in a C program
Earlier processors, such as CDC Cyber 18, which were developed in the 1980s, use one's complement. However, modern computer systems rarely use it.
Two's Complement
$$\bar{\alpha} = \tilde{\alpha} + 1 = 2^{n} - \alpha$$
$$\alpha + \bar{\alpha} = 2^{n}$$
The two's complement (TC) representation of a negative number is bitwise NOT of its positive counterpart plus one.
The opposite is also true. If we take bitwise NOT of a negative number and then add 1 to the result, we obtain the two's complement representation of its positive counterpart.
The following clarifies two confusing terms:
Convert x to two's complement: Find the two's complement representation of x without changing its value.
Calculate or take two's complement of x: Compute the negative of x.
For example, the following C program calculates two's complement of x.
y = ~x; // Toggle every bit
y += 1; // Obtain two's complement
Carry Flag for Unsigned Addition or Subtraction
Cortex-M processors maintain the application program status register (APSR). It holds important flags such as:
Carry flag (C)
Overflow flag (V)
Zero flag (Z)
Negative flag (N)
Saturation flag (Q)
Processors rely on these flags to evaluate whether any abnormal phenomenon occurs at runtime. For example, when two unsigned numbers are added, the carry flag indicates whether the sum is too large to fit into a 32-bit register.
Moreover, processors rely on these flags to implement branch instructions. In the below example, the compiler translates the if-else statement into conditional branch instructions, which check the flag bits to decide whether the processor should execute c =a - b or c = b - a.
if (a > b)
{
c = a - b;
}
else
{
c = b - a;
}
Depending on whether variables a and b are signed or unsigned, the compiler uses different assembly instructions to implement the if-else statement.
The carry flag is for operations on unsigned integers, and the overflow flag is for operations on signed integers.
Let us first review simple addition and subtraction of two integers with only one bit. The carry/borrow flag is set as shown below
| Addition | Subtraction |
| 0 + 0 = 0, Carry = 0 | 0 - 0 = 0, Borrow = 0 |
| 1 + 0 = 1, Carry = 0 | 1 - 0 = 1, Borrow = 0 |
| 0 + 1 = 1, Carry = 0 | 0 - 1 = 1, Borrow = 1 |
| 1 + 1 = 0, Carry = 1 | 1 - 1 = 0, Borrow = 0 |
In an n-bit system, a carry or borrow occurs under the following scenarios.
When two unsigned integers are added, a carry event takes place if the result is larger than the maximum representable unsigned integer
2^n - 1When two unsigned integers are subtracted, a borrow event occurs if the result is negative, smaller than the smallest expressible unsigned integer
0
While addition can modify the carry flag, subtraction can change the borrow flag. However, on ARM Cortex-M processors, the carry flag and the borrow flag are physically the same flag bit in the application program status register (APSR). Thus, the borrow flag is, in fact, called the carry flag.
On Cortex-M, the carry flag is set as follows:
When adding two unsigned integers, the processor sets the carry flag if a carry occurs, i.e., the sum is too large to be stored in a 32-bit register. Otherwise, the carry flag is cleared.
When subtracting two unsigned integers, the processor sets the carry flag if no borrow occurs, implying the difference is positive or zero. Otherwise, the carry bit is cleared.
For subtraction Carry = NOT Borrow.
Overflow Flag for Signed Addition or Subtraction
While the carry flag is for unsigned arithmetic operations, the overflow flag is for signed arithmetic operations. Overflow occurs when the result produced by an arithmetic operation falls outside the representable range [-2^n-1, 2^n-1 - 1] of two's complement.
When adding signed numbers, overflow occurs only in two scenarios:
Adding two positive numbers produces a non-positive result.
Adding two negative numbers yields a non-negative result.
Similarly, when subtracting signed numbers, overflow occurs in two scenarios:
Subtracting a positive number from a negative one creates a positive result.
Subtracting a negative number from a positive one makes a negative result.
Overflow cannot occur when operands with different signs are added or when operands with the same sign are subtracted.
Checking sign bits can detect overflow on addition. Overflow occurs on addition if the signs of the operands are the same, but the sum has a sign different from the operands.
In two's complement arithmetic, the problem of detecting overflow on subtraction can be converted to the issue of detecting overflow of addition. We can transform a subtraction operation into an addition operation. Algebraically, we have
$$A - B = A + (-B)$$
$$= A + TC(B)$$
where TC(B) takes the two's complement of B.
Thus, instead of performing subtraction, we add the negation of B to A. Therefore, the overflow flag of the original subtraction is set or cleared based on the addition result.
-9 - 6 = -9 + (-6) = 0b10111 + 0b11010 = 0b10001 = -15
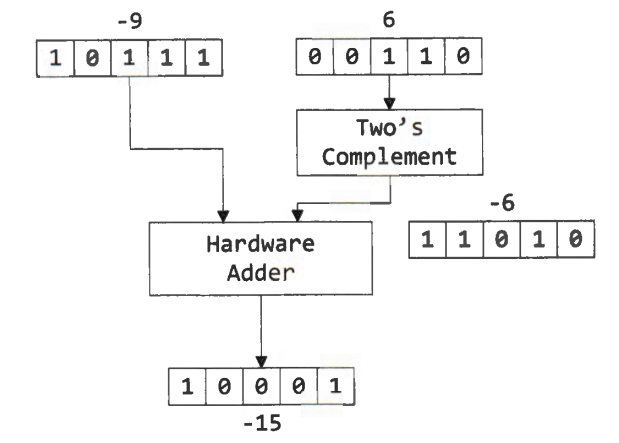
The hardware adder produces 0b10001, which equals -15 in two's complement. This shows that a signed subtraction can be successfully converted to a signed addition by taking the two's complement of the second source operand.
When adding 0b10111 and 0b11010, no overflow has occurred. Therefore, the overflow flag for the signed subtraction 0b10111 - 0b00110 is 0.
Overflow occurs on signed addition, if the carry into the sign bit differs from the carry out of the sign bit. Otherwise, there is no overflow.
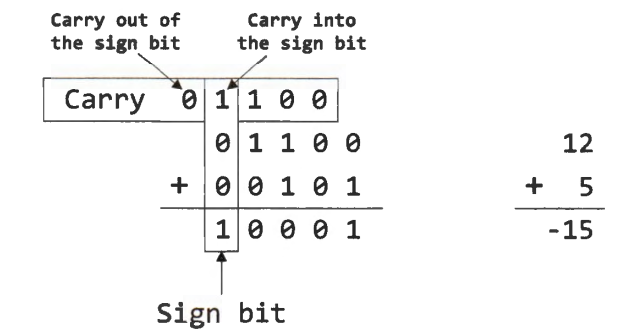
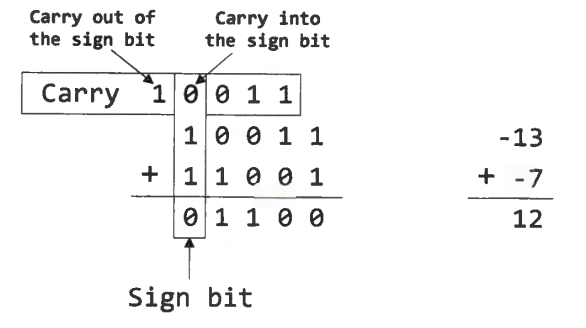
Interpreting the Carry and Overflow Flags
Is 0xFFFFFFFF a signed or unsigned number?
You and the compilers know the answer. But the processor does not know it at runtime.
Suppose in a five-bit system, the binary values of two variables are set as follows:
a = 0b10000
b = 0b10000
When adding these two numbers in an assembly program, should these two binary values represent signed or unsigned integers?
- If a and b are unsigned integers, we have:
a = 16
b = 16
a + b = 32 > 2^5 - 1
Thus, carry has occurred if a and b are unsigned integers.
- if a and b are signed integers, we have:
a = -16
b = -16
a + b = -32 < -2^4
Thus, overflow has occurred if a and b are signed integers.
Should the processor set up the carry flag or the overflow flag when a and b are added?
In fact, when adding these two numbers in an assembly program, the processor does not know whether a and b are signed or unsigned integers. Thus, the processor simply sets both the overflow flag and the carry flag. It is the assembly programmer's responsibility to interpret the flag results.
Assembly programs should appropriately choose to check either the overflow flag or the carry flag in assembly instructions, depending on the software's intention of using them as signed or unsigned integers.
For example, to evaluate the logical expression a+ b > 10, we should use different assembly instructions to check either the carry or overflow flag depending on whether a and bare unsigned or signed integers.
When interpreting the carry flag and overflow flag, one must be careful because they have different meanings for different operations. If the carry flag is set, it means the result is incorrect for addition but correct for subtraction. If the overflow is set, it means the result for both addition and subtraction is wrong. The table below summarizes the carry flag and the overflow flag for unsigned and signed addition/subtraction.
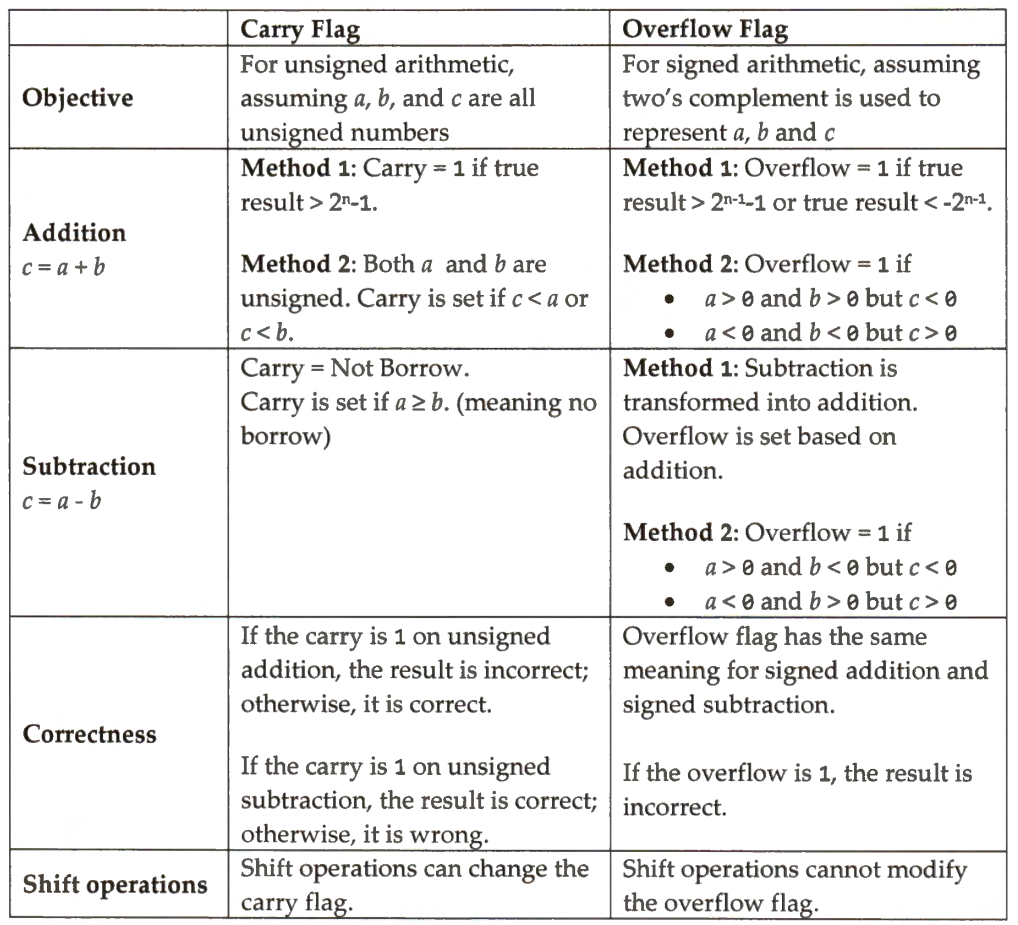
In C, variables a and b are declared explicitly either signed or unsigned by the programmer, such as unsigned int a or int a. Thus, the corresponding assembly program translated from the C program can correctly choose either the carry flag or the overflow flag to interpret the result.
Example: Translating the C statement if (a > b) into assembly
An if-statement in C is translated into a set of assembly instructions involving comparison and conditional branch. When translating if (a > b), C compilers must choose appropriate branch instructions by considering whether the logic expression compares two signed numbers or two unsigned numbers. When performing the comparison, the processor does not know whether they are signed or unsigned. Therefore, the processor hardware will write a value to the carry flag by assuming they are unsigned and simultaneously write a value to the overflow flag by assuming they are signed numbers. The software should choose the appropriate instructions to evaluate the carry flag or the overflow flag based on the following rules.
If variables a and b are declared as
unsignedin C, the compiler appends theHIcondition suffix to the branch instruction (i.e.,BHI), which checks the carry flag.If a and b are declared as
signed, the compiler appends theGTsuffix to the branch instruction (i.e.,BGT), which checks the overflow flag.
Although an if-statement is correctly translated to assembly instructions, most C compilers ignore the occurrence of the overflow and carry when an integer result falling out of the representable range is stored during data operations. In the following example, the leading bytes of the variable i are truncated, but the compiler might not generate any error message to abort compiling. This often leads to an unexpected or erroneous result. Failing to consider overflow and carry is a software bug often made by programmers.
/* Overflow and carry are ignored in C */
signed int i = 0x89ABCDEF; // 32-bit signed integer
signed short s = i; //overflow, s = 0xCDEF, variable i is truncated
signed char c = i; //overflow, c = 0xEF, variable i is truncated
Two's Complement Simplified HW Implementation
Two's complement simplifies the logic implementation of arithmetic functions. Binary data to be processed may be signed or unsigned integers. If two's complement is used to represent signed numbers, the hardware implementation becomes simple. The hardware does not need to worry about whether these operands are signed or unsigned, performs the same addition, subtraction, or multiplication operation, and still obtains the correct result.
Two's Complement Addition
The hardware adder designed for adding two unsigned numbers also works correctly for adding two signed numbers. For example, if two binary numbers, 0b10111 and 0b00110, are added in a five-bit system, the hardware adder performs a simple addition by treating them as unsigned numbers, and we obtain the sum as 0b11101.
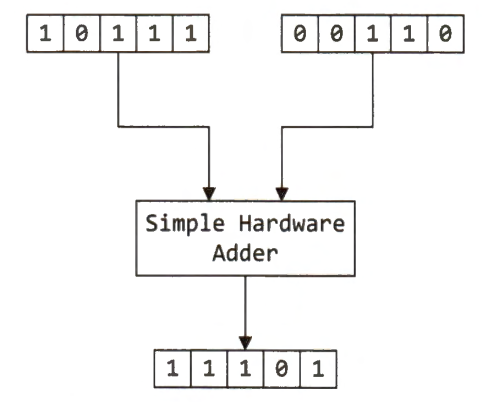
In fact, the binary number 0b11101 equals 29 if it is an unsigned number and -3 if it represents a signed number in two's complement. This implies that a simple adder, which does not distinguish the sign of its operands, can obtain the correct result. Therefore, the same hardware adder works correctly for both signed addition and unsigned addition.
Two's Complement Subtraction
The same subtraction hardware works correctly for both signed subtraction and unsigned subtraction. For example, when we subtract 0b00110 from 0b10111 in a five bit system, we obtain 0b10001.
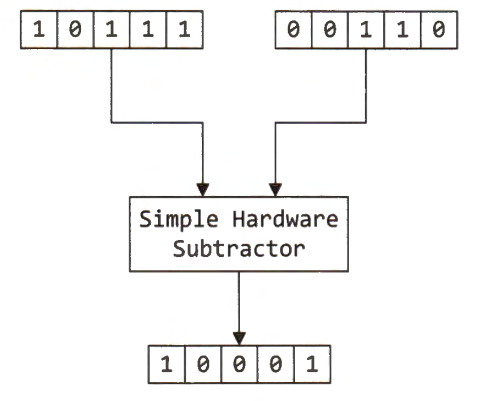
The binary result 0b10001 represents 17 if it is unsigned and -15 if it is signed in two's complement.
Two's complement multiplication
If the product is required to keep the same number of bits as operands, unsigned multiplication hardware works correctly for signed numbers. Given two binary numbers: 0b00011 and 0b11101, the hardware performs a simple multiplication. Since the product must be five bits, the product obtained is 0b10111, with extra leading bits truncated.
If both operands are signed, then in two's complement we have two operands as
0b00011 = 3,0b11101 = -3, and the result as0b10111 = -9.On the other hand, if both operands are unsigned, then we have two operands
0b00011 = 3and0b11101 = 29, and the result0b10111 = 23. While the result is incorrect, it does not mean the hardware has failed. It is only because the result is too large and cannot be fully expressed with 5 bits. To avoid this issue, software should use a more complex multiplication instruction to multiply two large numbers.
On many processors, multiplication instructions do not affect the carry and overflow flags. On ARM Cortex-M, a multiplication instruction leaves the carry flag undefined and the overflow flag unchanged.
Two's complement division
However, signed and unsigned division cannot directly share the same division hardware. For example, we divide -10 (0b10110 in two's complement) by 2 (0b00010 in two's complement) by using a traditional division technique, the quotient obtained is 11 (0b01011 in two's complement). Apparently, the conventional division for unsigned integers does not work for signed integers.
Signed division is harder than unsigned division. A general method of signed division is first to convert both signed numbers to positive numbers, then execute unsigned division, and finally change the result into signed form.
Therefore, there are two 32-bit integer division instructions in Cortex-M processors. The SDIV instruction is signed division, and the UDIV instruction is unsigned division.
Subscribe to my newsletter
Read articles from Ahmed Gouda directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Ahmed Gouda
Ahmed Gouda
Embedded Software Engineer who are interested in Embedded Systems Design, Embedded Software, Electrical Engineering, and Electronics, C\C++ programming, Assembly, Computer Architecture, Microprocessors, Microcontrollers, and Communication Protocols.