Recursion
 Chetan Datta
Chetan Datta
Introduction
Recursion
When a function calls itself
until a specified condition is met.
f(){
print(1);
f();
}
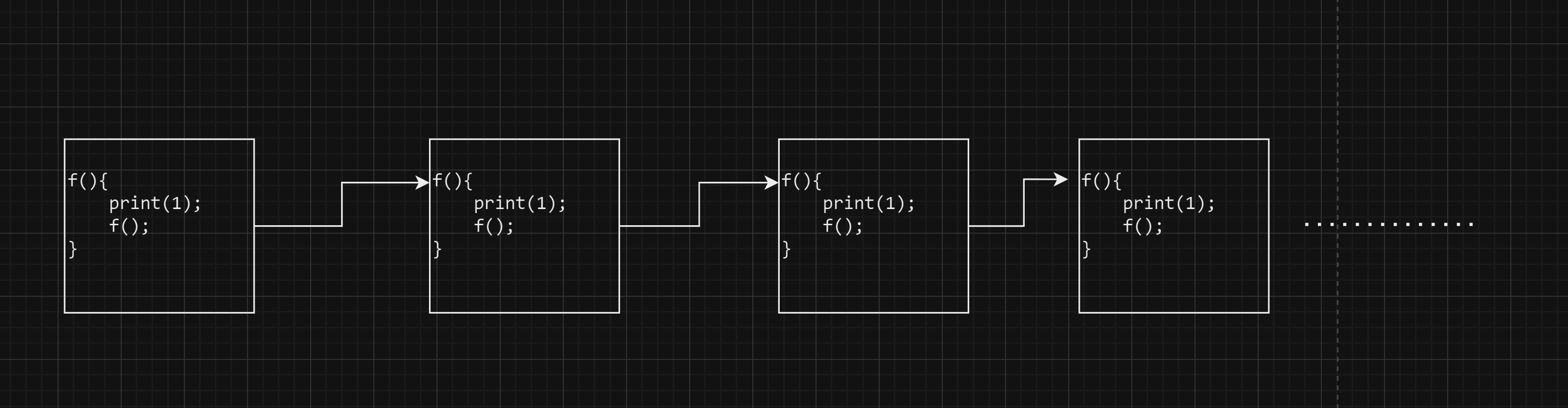
Stack Space
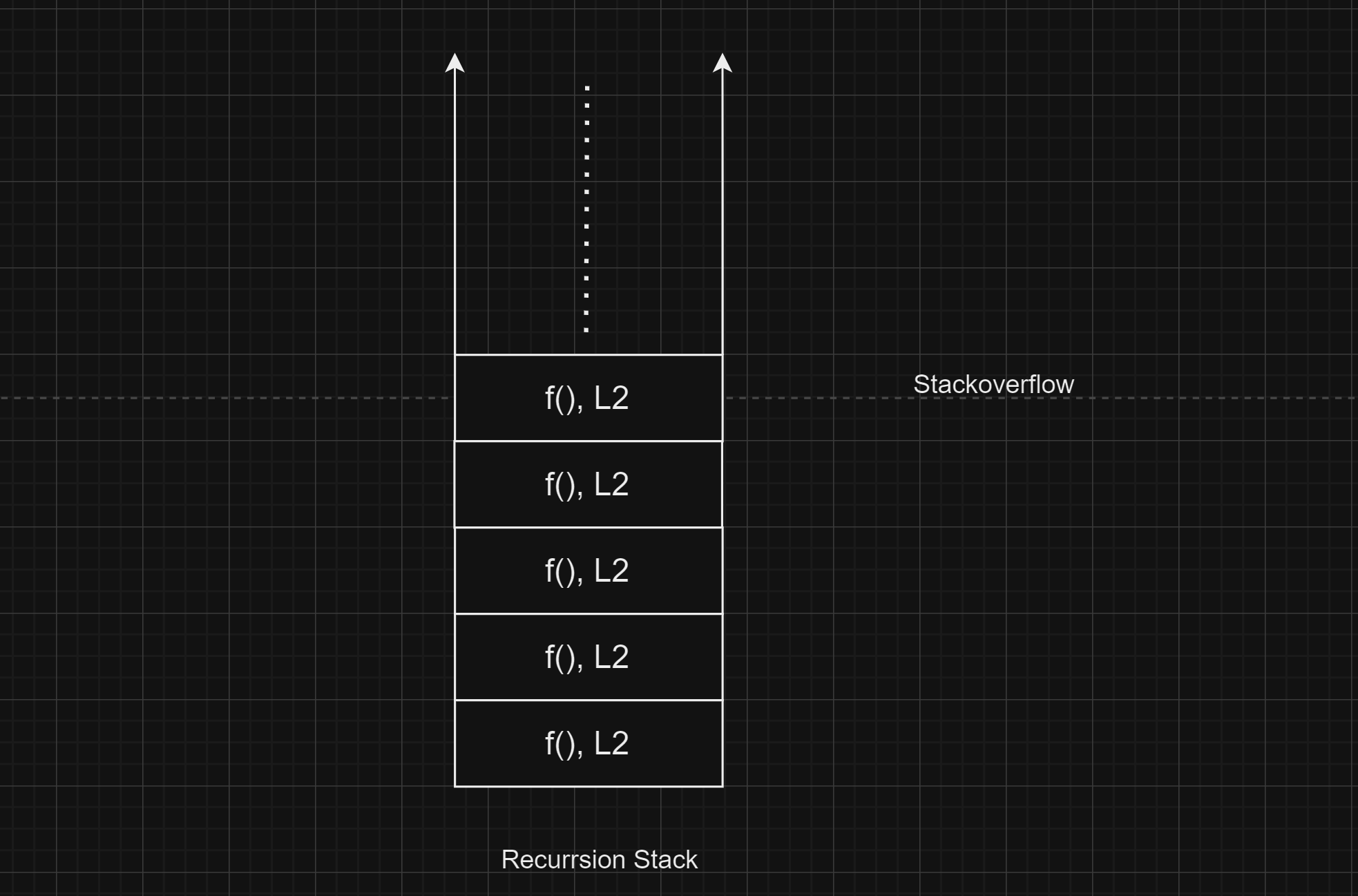
Base Case
The condition that stops the recursion is called the base case.
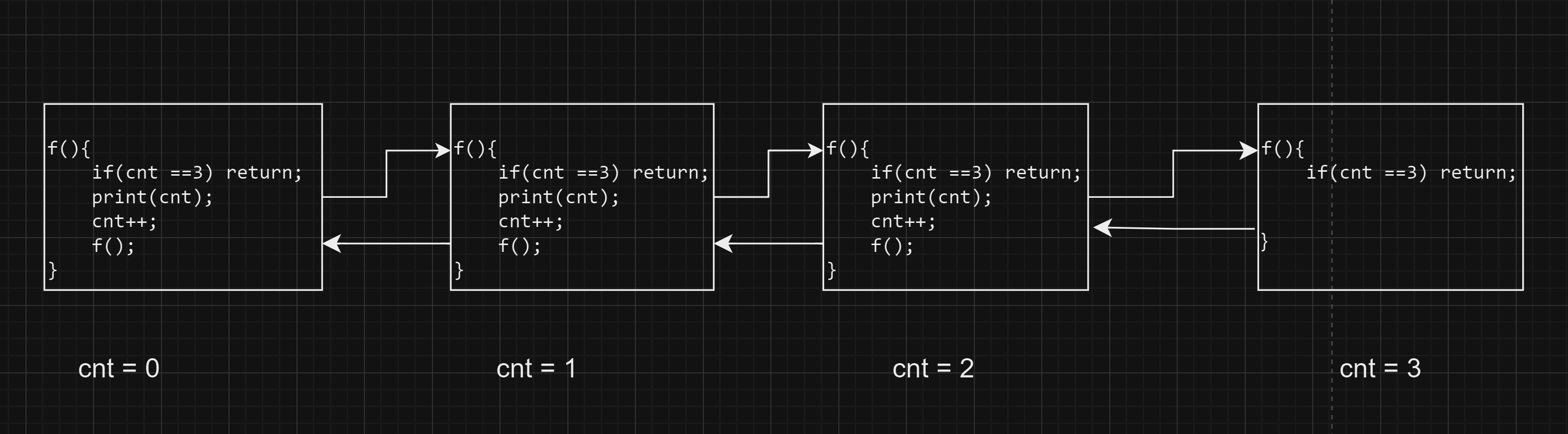
//cnt is a global variable
f(){
if(cnt ==4) return;
print(cnt);
cnt++;
f();
}
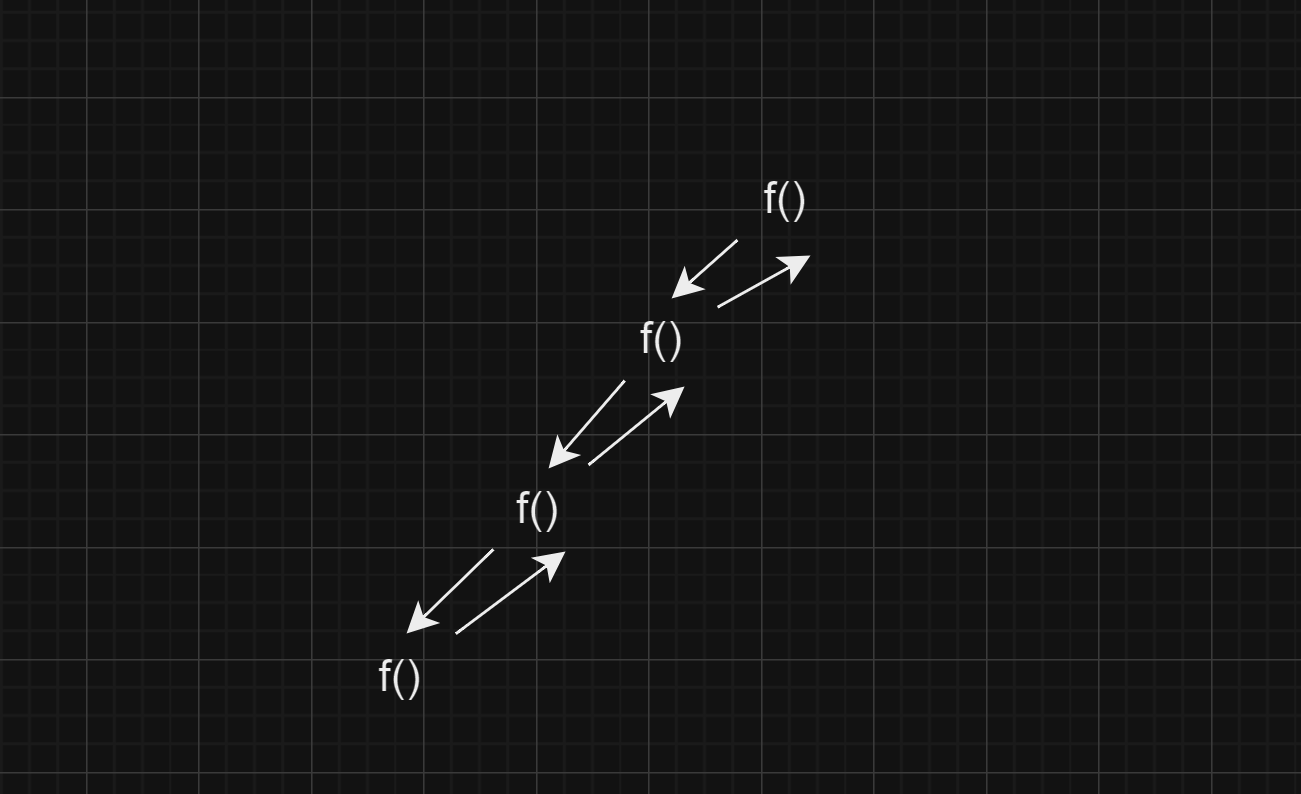
Recursion Tree
Instead of showing the entire code in each step of recursion, we can simplify it by using just the function name and visualizing this as a recursion tree.
Basic Problems
Print Name 5 times
public void f(int i, int N){
if(i>N) return; //Base Condition
System.out.print("name");
f(i+1,N);
}
public static void main(String args[]){
int n = 3;
f(1,n);
}
Print linearly from 1 to N
public void f(int i, int N){
if(i>N) return;
System.out.println(i);
f(i+1,N);
}
//f(1,N)
Print from N to 1
public void f(int i, int N){
if(i<1) return;
System.out.println(i);
f(i-1,N);
}
//f(N,N)
Backtracking
Print Linearly from 1 to N
public void f(int i, int N){
if(i<1) return;
f(i-1,N);
System.out.println(i);
}
//f(N,N)
Print from N to 1
public void f(int i, int N){
if(i>N) return;
f(i+1,N);
System.out.println(i);
}
//f(1,N)
Difference between forward-tracking and Back tracking
Forward-Tracking: In this approach, we complete the execution of all statements in the current step before making the recursive call. This means we finish each step entirely before moving on to the next one.
Backtracking: Here, we make multiple recursive calls from the first step to the last without completing the current step. Once we reach the last step, we start finishing each step in reverse order, moving back to the first step.
Note: Forward-Tracking + BackTracking both exists in any recursion.
Types of Recursion
Parameterized Recursion
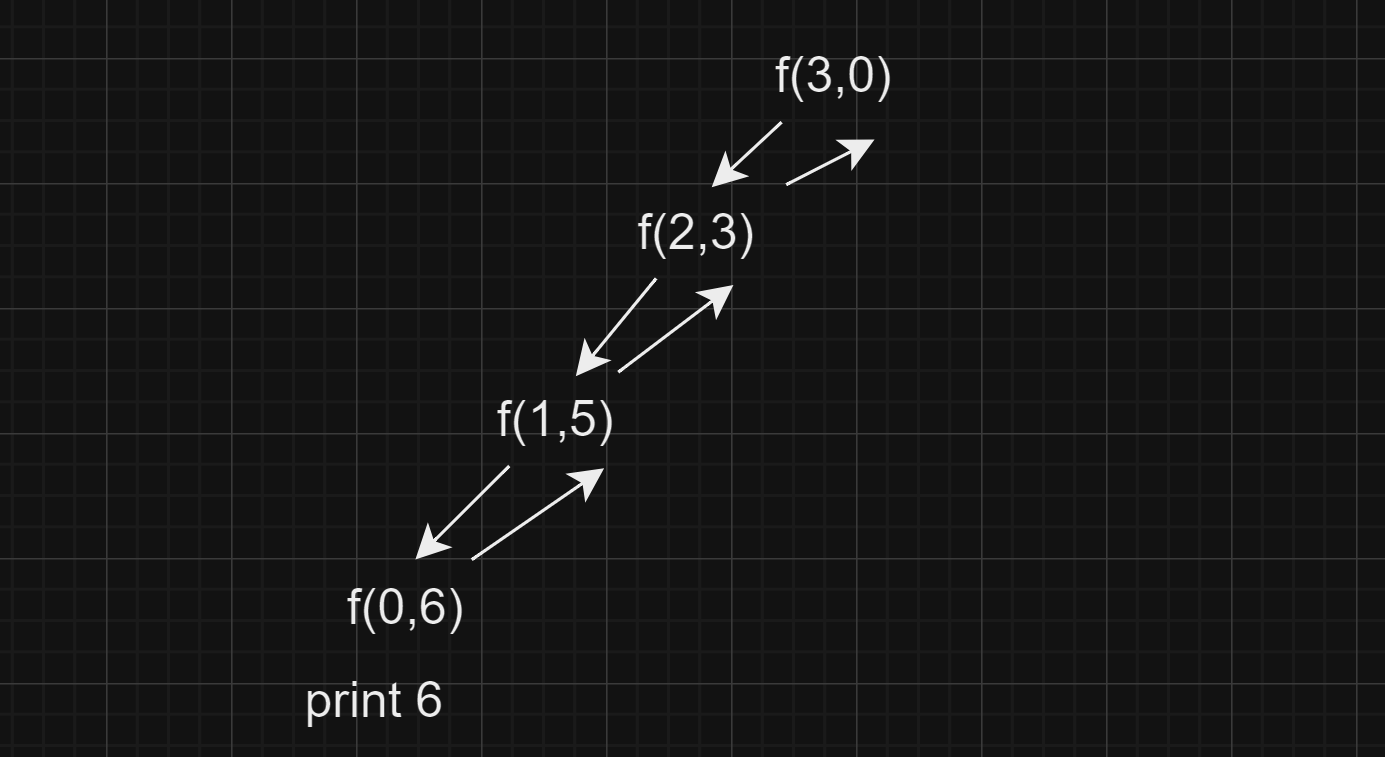
Sum of n natural numbers
f(i,sum){
if(i<1) {
print(sum);
return;
}
f(i-1, sum+i);
}
//f(n,0)
Functional Recursion
Sum of n natural numbers
f(n){
if(n==0) return 0;
return n + f(n-1);
}
//f(n)
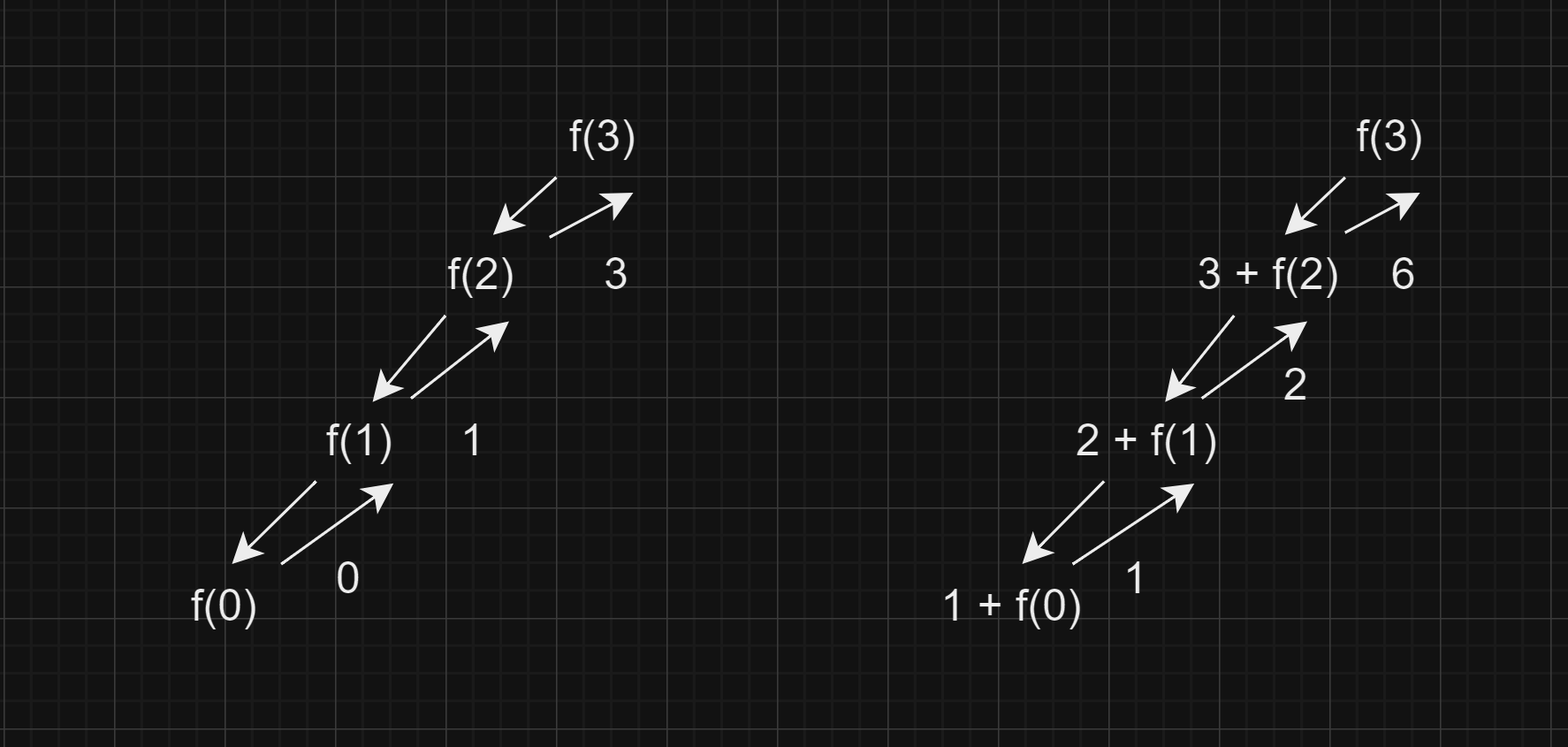
Factorial of n
fact(n){
if(n==0) return 1;
return n * fact(n-1);
}
//fact(n)
Problems on Functional Recursion
Reverse an Array
We place two pointers, left (l) and right (r), at the start (index 0) and end (index n-1) of the array, respectively. We then swap the elements at these pointers, increment left by 1, and decrement right by 1. This process continues until left surpasses or equals right.
f(l,r){
if(l>=r) return;
swap(a[l],a[r]);
f(l+1,r-1);
}
//f(0,n-1);
f(i){
if(i>=n/2) return;
swap(a[i],a[n-1-i]);
f(i+1);
}
//f(0);
Pallindrome
To check if a string ( s ) is a palindrome, we compare the character at index ( i ) with the character at index ( n-1-i ). We increment ( i ) from 0 to ( n/2 ) (the midpoint). If all corresponding characters match, we return true; otherwise, we return false.
f(i){
if(i>=n/2) return true;
if(s[i]!=s[n-1-i]) return false;
return f(i+1);
}
//f(0);
Valid Pallindrome - Leetcode
A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string s, return true if it is a palindrome*, or* false otherwise. (link)
"A man, a plan, a canal: Panama"
Output: true
Explanation: "amanaplanacanalpanama" is a palindrome.
Solution
class Solution {
public boolean findOutPalindrome(int i, String s){
int n = s.length();
if(i>=n/2) return true;
if(s.charAt(i)!=s.charAt(n-i-1)) return false;
return findOutPalindrome(i+1, s);
}
public boolean isPalindrome(String s) {
s = refineString(s);
return findOutPalindrome(0, s);
}
public String refineString(String s){
//a-z 97<->122
//0 - 9 48<->57
//space - 32
// int n = (int) ' ';
// System.out.println(n);
s = s.toLowerCase().replaceAll("\\s","");
StringBuilder root = new StringBuilder();
for(char ch : s.toCharArray()){
int ascii = (int) ch;
if((97<=ascii && ascii<=122) || (48<=ascii && ascii<=57)){
root.append(ch);
}
}
return root.toString();
}
}
Multiple Functional Recursion Calls
If a function calls itself multiple times within its body, it is considered to be making multiple recursive calls.
f(){
...
...
f()
...
...
}
Fibonacii Number
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is, (link)
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).
Example 1:
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Solution
- Pseduo code
f(){
if(n<=1) return n;
last = f(n-1)
slast = f(n-2)
return last+slast;
}
- Code
public int fib(int n) {
if(n<=1) return n;
return fib(n-1) + fib(n-2);
}
Recursion Tree - Multiple recursion calls
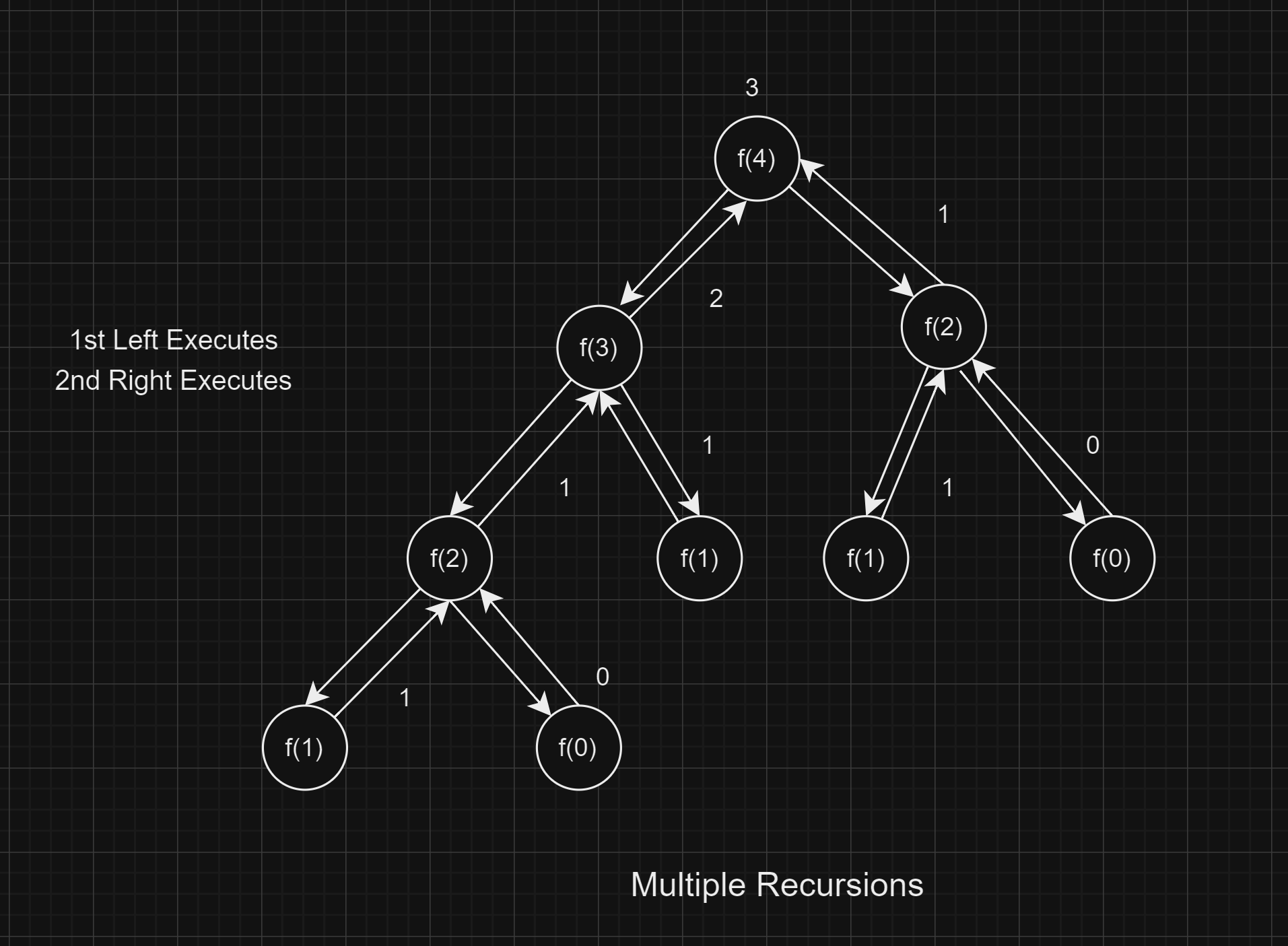
Time Complexity - O(2^n)
The function f(n) requires 2 calls, f(n-1) also requires 2 calls, and f(n-2) needs 2 calls as well. Therefore, the total number of calls is ( 2 x 2 x ..... ) (n times), which equals 2^n. However, it takes fewer than 2^n calls because the second call reduces the problem size from n to n-2.
Subscribe to my newsletter
Read articles from Chetan Datta directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Chetan Datta
Chetan Datta
I'm someone deeply engrossed in the world of software developement, and I find joy in sharing my thoughts and insights on various topics. You can explore my exclusive content here, where I meticulously document all things tech-related that spark my curiosity. Stay connected for my latest discoveries and observations.