Mastering Lexical and Syntax Analysis: An Exploration of Tokenizers and Parsers
 arman takmazyan
arman takmazyan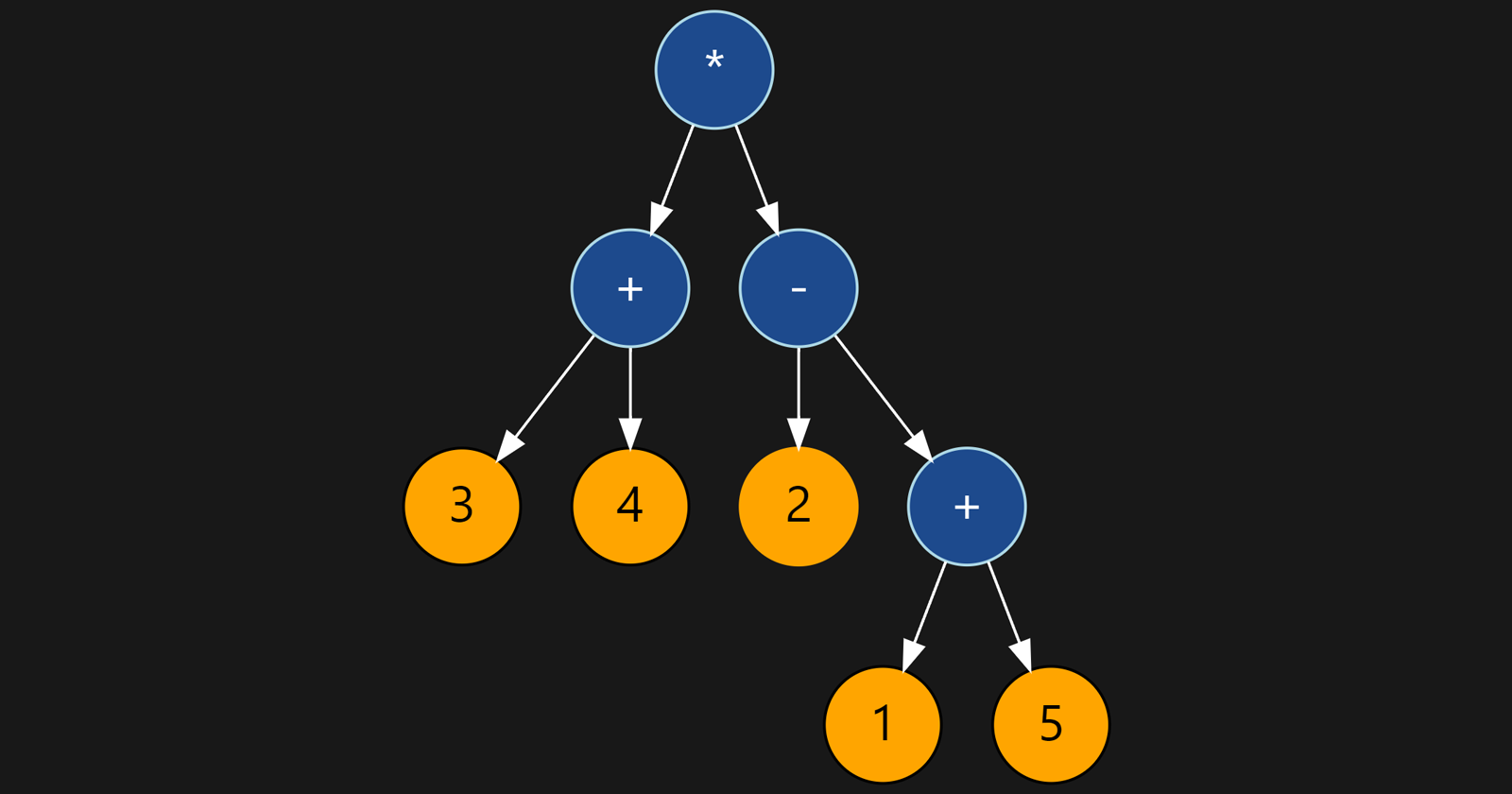
Previous Posts:
Creating TuffScript: Exploring Esoteric Programming Languages and Their Foundations
Mastering Formal Grammars: An Introduction to the Chomsky Hierarchy
Precedence and Associativity in Grammar Rules
Lexical analysis
After defining the grammar for our language, the next step is to create a Tokenizer.
We use the following definitions:
A lexeme is a sequence of characters that matches the pattern for a token and is identified as that token's instance.
A pattern describes the possible forms of a token's lexemes.
Token is a pair consisting of a token name and an optional token value. The token name is a category of a lexical unit.
A lexical analyzer, also known as a tokenizer, is a program that receives text and creates tokens.
| Token Name | Lexeme |
| number | 2 |
| multiplicationOperator | * |
| number | 2 |
| additionOperator | + |
| number | 5 |
In this example, the arithmetic expression '2*2+5' is segmented into tokens. Each token type (number, multiplicationOperator, additionOperator) corresponds to a lexeme ('2', '*', '2', '+', '5'), which are the actual characters and symbols in the expression.
The Tokenizer doesn't figure out what the text means. Its job is to make the text easy to handle for the next steps, like understanding the structure and meaning of the text.
We could choose not to use a Tokenizer. This might be an option for very simple programs, like a basic arithmetic expressions evaluator. However, for more complex situations, such as creating an interpreter for a programming language, it's essential to use a tokenizer. It helps break down and analyze text more easily, making our work simpler and more organized.
Technically, the objects representing the tokens can also include metadata. For instance, they can store the token positions. The position of tokens is crucial for error handling and linting. In general, it is a good idea to include metadata that we can utilize for various text analysis methods.
Syntax analysis
The next step in processing text is parsing. Syntax analysis, also known as parsing, is the process where we check if the source code follows the grammatical rules of the language. During parsing, the sequence of tokens produced by tokenization is analyzed to understand their syntactic relationships. The result of this syntactic analysis is a parse tree, often referred to as a concrete syntax tree (CST). A concrete syntax tree is a hierarchical structure that represents the relationship between a given sequence of tokens, showing how they relate to each other in terms of syntax.
Imagine a tree that represents a sentence. Each branch and leaf of the tree is a part of the sentence, like words and punctuation. The CST shows every part of the sentence and how they are connected, in the exact order they appear. It includes every detail, even small ones that don't change the sentence's overall meaning. This tree helps us see how the sentence is put together, piece by piece, like a detailed map.
There are two main ways to create a parse tree: the top-down approach and the bottom-up approach. We will use the principles of leftmost and rightmost derivation in order to understand how to build a parse tree.
Top-down parsers typically operate under the assumption that the derivation of a string from the grammar can be performed using leftmost derivation, where at each step, the leftmost non-terminal symbol is expanded. The tree construction process for these parsers can be visualized as follows:

You can see that it directly reflects the process of derivation, proceeding from top to bottom and from left to right.
In a rightmost derivation, the grammar's production rules are applied in such a way that at each step, the rightmost non-terminal in the string is replaced first. This process continues until the string is fully derived from the start symbol. The bottom-up parsing technique mirrors this process backward by beginning with the input (which can be seen as the end result of a rightmost derivation) and progressively reducing it to the start symbol through the application of production rules in reverse. Reduction is the opposite of derivation.

It is also known as shift-reduce parsing, which constructs a parse tree for an input string by starting from the leaves (the input tokens) and working its way up to the root (the start symbol).

During bottom-up parsing, each shift operation corresponds to moving forward in the input string, effectively "recognizing" terminal symbols (the leaves of the parse tree). The reduce operation then applies a production rule in reverse, replacing a sequence of symbols on the stack (which corresponds to the right-hand side of a production rule) with the non-terminal on the left-hand side of that rule. This step is equivalent to one step back in the rightmost derivation process, hence the description of bottom-up parsing as executing a rightmost derivation in reverse. Through a series of shift and reduce operations, the parser reconstructs the original derivation from the input back to the start symbol, thereby parsing the input according to the grammar.
Now that we understand the general approaches to parsing grammars, we can move on to creating a diagram of parser types. This diagram will help us visually explore the relationships between different parser types. It's important to note that, in reality, the variety of parsers is vast, and not all will be covered in our diagram. However, the ones we will discuss represent the core variations, encompassing the essential features of most parser types.
As we have already seen, there are two major types of parsers: Top-Down parsers and Bottom-Up parsers. Top-Down parsers can be further divided into those with backtracking and those without backtracking.
Backtracking means that the parser can revisit and apply different production rules if the initial rule does not lead to a correct solution. It's like retracing steps to find the right path after reaching a dead end. This approach might seem to offer greater flexibility, but it can actually make the parsing logic more complicated in practice and increase processing time.
Consider the following grammar:
S → aAb
A → cd | c
Using the target string "acb", let's go step by step to see how a top-down parser with a backtracking approach works.
Parsing Steps:
Start with the start symbol, S.
S → aAb means the string must start with "a", have some derivation of A in the middle, and end with "b".
We match the first "a" of the string "acb" with the "a" in the rule S → aAb.
Now, we need to match A and then "b". According to the rules for A, A can be replaced by "cd" or "c". We first try the option A → cd.
- Attempt 1: Replace A with "cd" (A → cd). We get "acd", which does not match "acb". This path leads to a dead end.
Since the first choice led us to a dead end, we use backtracking to go back to the point where we chose the rule for A.
Now, we try the second option for A, which is A → c.
- Attempt 2: Replace A with "c" (A → c). Now we have "ac" from S → aAb with A replaced by "c", and then we add "b" at the end as specified by S → aAb.
We successfully match the string "acb" with the grammar by following the sequence aAb, choosing A → c, and finally matching the entire string.
Through this process, backtracking allowed us to reconsider our choice for A when the first option led to a mismatch, enabling us to find the correct path that matches the string "acb" to the provided grammar.
![]()
In the case of parsing the string "acb" with the given grammar using a predictive parser, the process differs slightly from the backtracking approach. Predictive parsers are a type of top-down parser that rely on looking ahead at the next input symbols and use decision-making rules (often in the form of parsing tables) to determine which production rule to apply. They do not use backtracking. Instead, they choose the correct production based on the current input symbol and the grammar rules.
Let's see how the parsing steps for the same string look when we utilize predictive parsing:
The parser starts with the procedure for S since it's the start symbol. It matches the first symbol of the input, "a", directly.
Before calling the procedure for A, the parser looks at the next symbol in the input, which is "c". Here, the parser needs to decide which version of A to use (A → cd or A → c). Using lookahead, the parser sees that the symbol following "c" is "b". This information is crucial because:
If the parser were to choose A → cd, it would expect a "d" after "c", but the next symbol is "b", not "d". This choice would lead to a parsing error.
Therefore, the parser correctly decides to use A → c, because it matches the current symbol "c" and anticipates that the string can be correctly continued with the remaining input "b".
The parser calls the procedure for A, choosing A → c based on the lookahead.
After successfully parsing "a" and "c" with the rules S → aAb and A → c, the parser then matches the final symbol "b" in the input with the "b" in the rule S → aAb.
In summary, a predictive parser would parse the string "acb" efficiently by using lookahead to make decisions on which production rules to apply at each step, directly leading to a successful parse without the need for backtracking.
These algorithms can be implemented with recursion or with a table-driven approach. That's why it's important to understand that the division between backtracking and predictive characterizes the algorithm, while the division between recursive and table-driven characterizes the implementation. However, the table-driven approach is generally associated with predictive parsers (like LL parsers), which don't use backtracking because they rely on lookahead and parsing tables to decide which rule to apply.
Recently, I've found a really good visualizer for top-down predictive parsers with a table-driven approach:
https://www.cs.princeton.edu/courses/archive/spring20/cos320/LL1/
You can try it out and see how it works. You'll notice that the tree construction process is quite similar to the visualization we looked at earlier.
Although we’ll be using a recursive parser without backtracking to create our arithmetic expressions evaluator and TuffScript, which constructs the tree a bit differently (we’ll explore this later), it's valuable to understand how the table-driven approach works.
I also recommend checking out the "Introduction to Parsers" from Neso Academy, which explains how parsing tables are created for top-down predictive parsers:
Our parser types diagram now looks like this:
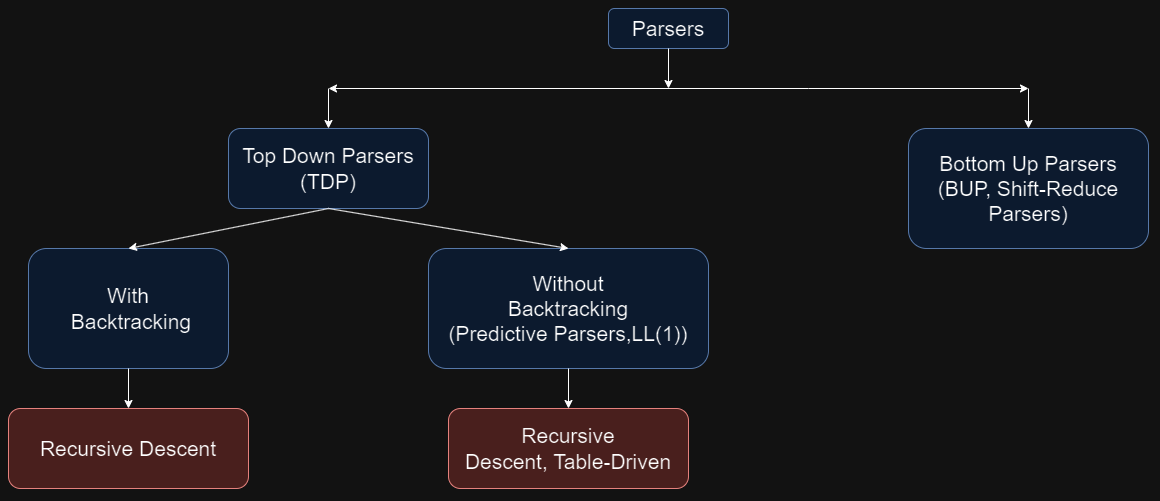
Regarding terminology in LL(k) parsers:
The first "L" stands for reading the input from left to right.
The second "L" represents producing a leftmost derivation.
The "(k)" indicates the number of lookahead tokens the parser uses to make decisions about which rule to apply at any point.
LL(1) parsers are popular because they balance simplicity and effectiveness well. Using just one lookahead token (k=1), they can make most parsing decisions easily, keeping things straightforward. Adding more lookahead tokens (increasing k) makes both the parser and the grammar more complex, which can make parsing harder and the grammar more complicated to design.
Let's now see what kinds of parsers we have for the bottom-up approach:
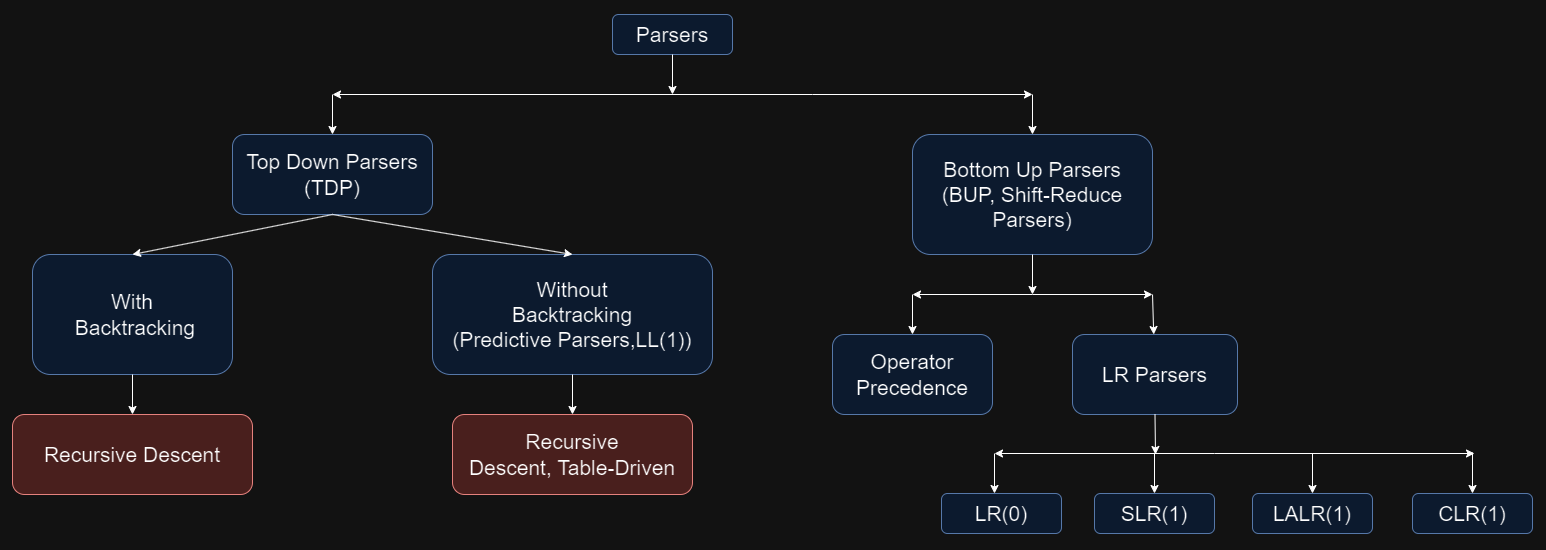
Operator precedence parsers are designed for specific types of grammars that must meet two main properties:
No right-hand side (R.H.S.) of any production contains an epsilon (empty string).
No two nonterminals are adjacent in any production.
Operator precedence parsers can handle ambiguous grammars by using a hierarchy of operations to determine the order of execution. This method resolves ambiguities by assigning priority to specific operations, enabling the parsing of expressions that might have multiple interpretations. This capability distinguishes them from other parsers that require grammars to be unambiguous to parse expressions effectively.
Regarding terminology in LR(k) parsers:
The "L" stands for reading the input from left to right.
The "R" represents producing a rightmost derivation in reverse.
The "(k)" indicates the number of lookahead tokens the parser uses to make decisions about which rule to apply at any point.
All LR(0), SLR(1) (Simple LR), LALR(1) (Look-Ahead LR), and CLR(1) (Canonical LR) parsers are types of shift-reduce parsers. They utilize parsing tables to analyze grammars. The primary differences among them lie in how their parsing tables are constructed and in their complexity levels.
Since we will be creating a recursive descent parser, you can find more information about bottom-up parsers (and parsers in general) in the book Parsing Techniques: A Practical Guide by Dick Grune and Ceriel J.H. Jacobs.
Using the arithmetic expressions grammar we previously created, the concrete syntax tree for the expression "2 * 2 + 5" will appear as follows:
The root of the tree is the <expression>, which in our case is <term> + <term>.
The first <term> is 2*2, which breaks down into <factor> * <factor>.
- Each <factor> here is a <number>, which is a <digit>.
The second <term> is 5, which is a <factor>.
- The <factor> is a <number>, which is a <digit>.
The structure of a CST is a direct reflection of the rules used in the grammar of the language.
CSTs include every detail from the source code, such as parentheses, delimiters, and other syntax tokens, even if they don't contribute to the semantic meaning.
Concrete syntax trees include many details necessary for clearly understanding the source text, although these details don't always relate to the text's actual meaning. To manage the order of operations like addition and multiplication, the grammar uses different levels of expression parts. However, for actual interpretation, it is usually enough to have nodes in the tree that show the operations and their components.
This is where the abstract syntax tree (AST) comes into play. It is a simpler version of the concrete tree, retaining only the essentials to convey the program's meaning. ASTs typically remove redundant information like parentheses or specific details of the syntax that don't affect the semantic meaning of the language. This makes it easier to work with during the later stages of the program's execution. ASTs are commonly used in compilers and interpreters for further analysis, optimization, and code generation.
So the difference between an Abstract Syntax Tree (AST) and a Concrete Syntax Tree (CST), also known as a Parse Tree, lies in the level of abstraction and the type of information they contain about the source code or expression they represent.
The call stack of the recursive descent parser implicitly forms a Concrete Syntax Tree (CST), which is naturally constructed in memory while the parser works to recognize a specific language construct. This characteristic is specific to recursive descent parsers, where each recursive call corresponds to a node in the CST. However, other types of parsers, such as shift-reduce parsers, construct the CST using different mechanisms and do not rely on the call stack.
Interpreter
After parsing an arithmetic expression into an AST (Abstract Syntax Tree), the evaluation process begins.
Evaluation is the process of reducing an expression to a single value. This expression typically consists of a sequence of operands and operators.
Each node in the AST represents a component of the expression, such as a number or an operator. The interpreter processes these nodes, starting from the leaves (outermost nodes) and working towards the root.
When the interpreter encounters an operator node (e.g., +, -, , /), it applies this operation to its child nodes, which are usually numbers or results from other sub-expressions. The traversal order through the AST depends on the rules of operation precedence and association in arithmetic. For instance, in the expression 3+2*4, the multiplication (*) is prioritized over addition (+), leading to the evaluation of 2 * 4 before adding 3.
The interpreter continues to traverse and evaluate all nodes until it reaches the root of the AST. At this point, the final result of the expression is computed. If the AST includes any invalid operations, the interpreter identifies and addresses these errors during traversal, ensuring accurate and reliable evaluation of the expression.
What is interesting is that we can imagine ASTs as multidimensional lists. Each node in an AST corresponds to a list element, while the relationships between nodes are nested lists. This representation captures the hierarchical structure of program syntax. In this case, we can imagine the evaluation process as a sequential reduction of the list expressions.

In this way, we have actually created a dialect of the Lisp programming language.
Conclusion
Understanding lexical and syntax analysis is essential for grasping how programming languages function. With this knowledge, we're one step closer to building a real parser for our arithmetic expressions evaluator. Stay tuned for the upcoming chapters, where we’ll continue to explore and develop the skills needed to bring our parser to life!
Subscribe to my newsletter
Read articles from arman takmazyan directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

arman takmazyan
arman takmazyan
Passionate about building high-performance web applications with React. In my free time, I love diving into the fascinating world of programming language principles and uncovering their intricacies.