Applying Monte Carlo Simulation Methods to NS&I Premium Bonds
 Jason Shiers
Jason Shiers
This article is the first in a series that takes an in-depth look at using Monte Carlo simulations for NS&I Premium Bonds in the UK. It covers prize distribution and winning odds, and explains how to use Monte Carlo methods to simulate prize draws and estimate median returns for different bond holding sizes and durations. The simulation code is written in Python, using random sampling techniques and efficient computing methods to explore realistic outcomes for bondholders.
Introduction to Monte Carlo Simulation
Monte Carlo simulations use repeated random sampling to derive numerical results. Named after Monte Carlo Casino in Monaco, this method was developed by physicist Stanislaw Ulam, who drew inspiration from his uncle's gambling habits.
The method works by taking a variable with uncertainty and assigning it a random value. This value is used to compute an outcome using a model. The process is repeated multiple times with different random values. The results can then be used to determine a probability distribution for the outcome.
According to the Wikipedia article on the subject, the Monte Carlo approach can be applied to three main problem classes: optimisation, numerical integration, and generating draws from a probability distribution. This article will focus on the third of these problem classes.
Introduction to NS&I Premium Bonds
National Savings & Investments (NS&I) is the UK's government-backed savings institution. You can find more information about it here. It offers a variety of savings products to UK consumers. Among these, Premium Bonds stand out as the most popular savings product in the UK.
Premium Bonds are considered a savings product. You can put money into your Premium Bond account and take it out when you want. Instead of earning traditional interest, your returns are determined by a monthly prize draw. Each £1 bond has an equal chance of winning a prize, with amounts ranging from £25 to a jackpot of £1 million. Prizes are allocated by a random number generator named ERNIE (Electronic Random Number Indicator Equipment).
NS&I publishes a 'prize rate', which is the closest equivalent to an interest rate for Premium Bonds. This prize rate describes the mean annual return based on the total prizes awarded and the total number of Premium Bonds issued. However, this rate does not accurately reflect what an average person might win. The odds of winning with a single bond are low (21,000 to 1 at the time of writing), and the smallest prize available is £25. Smaller prizes are much more common than larger ones. Therefore, individuals with a small Premium Bond holding are very unlikely to win anything, and even with a larger holding, the chances of winning one of the top prizes remain extremely slim.
A better way to understand what an average person might win is to look at the median return. This is done by taking a group of people, tracking their winnings, and then ranking them from highest to lowest to see what the person in the middle has won. For a single Premium Bond in a single prize draw, the odds of winning anything are very low, and the median return is zero. The odds of winning improve by increasing the number of bonds held and by holding the bonds for a longer period to participate in more draws. Since the smallest prize is £25, the median winnings can only increase in £25 increments. As more bonds are held for longer, the chances of winning each prize increase. The median return will therefore tend towards the prize rate (mean return). The key questions are: what does that relationship look like, and what are the median returns at various holding sizes and durations?
Premium Bond Characteristics
As mentioned above, the odds of winning a prize with a single bond has been set to 21,000 to 1 at the time of writing. This prize rate is varied from time to time in line with changes to rates in the UK savings market. The breakdown of prizes is also varied. The projected prize matrix for the September 2024 draw is as follows:
| Prize Band | Prize Value | Number on offer |
| Higher (10% of prize fund) | £1 million | 2 |
| £100,000 | 87 | |
| £50,000 | 175 | |
| £25,000 | 350 | |
| £10,000 | 874 | |
| £5,000 | 1,747 | |
| Medium (10% of prize fund) | £1,000 | 18,269 |
| £500 | 54,807 | |
| Lower value (80% of prize fund) | £100 | 2,190,094 |
| £50 | 2,190,094 | |
| £25 | 1,475,218 | |
| Total prizes | 5,931,717 | |
| Total value | £456,742,050 |
There are a few things to note about the above table. First, consider the scale of this operation. With odds of winning set at 21,000 to 1 and 5,931,717 prizes available, the total number of bonds issued is 124.6 billion. The largest prizes make up 10% of the prize fund but only 0.05% of the prizes available. The chance of a bond winning one of the two jackpot prizes is just 2.96 million to 1, and the odds of any bond winning the jackpot are 62 billion to 1. The jackpot makes up 0.4% of the prize fund, while the other large prizes each make up a little under 2%.
A winning bond is much more likely to win a lower prize. There is a 37% chance of winning a £50 prize, the same chance of winning a £100 prize, and a 25% chance of winning a £25 prize. These three lower-value prizes make up 99% of the total prizes. In terms of the prize fund, 48% is in £100 prizes, 24% in £50 prizes, and 8% in £25 prizes.
Based on this initial appraisal, starting with holding 1 bond and then increasing the holding size and/or period, the median prizes won should initially be zero and stay at zero for some time. Then, the value should increase relatively quickly in £25 increments up to an 80% winning rate. After that, the second phase of the curve would gradually approach the prize rate but is unlikely to reach it within a realistic holding size and time frame. Therefore the prize rate is likely to create a misleading impression of what could be won by someone with average luck.
Given the large numbers involved, calculating the precise odds of winning using algebra and probability theory is incredibly complicated. A simpler option, though computationally intensive, is to do this numerically using a Monte Carlo approach.
Solving the problem numerically
Initial analysis of the problem
Let's look at the distribution of prizes graphically:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
PRIZE_MATRIX = {
25: 1_475_218, 50: 2_190_094, 100: 2_190_094,
500: 54_807, 1_000: 18_269, 5_000: 1_747,
10_000: 874, 25_000: 350, 50_000: 175,
100_000: 87, 1_000_000: 2
}
df = pd.DataFrame.from_dict(PRIZE_MATRIX, orient='index',
columns=['Frequency'])
sns.barplot(x=df.index, y=df['Frequency'])
plt.yscale('log')
plt.xlabel('Prize Value')
plt.ylabel('Frequency')
plt.show()
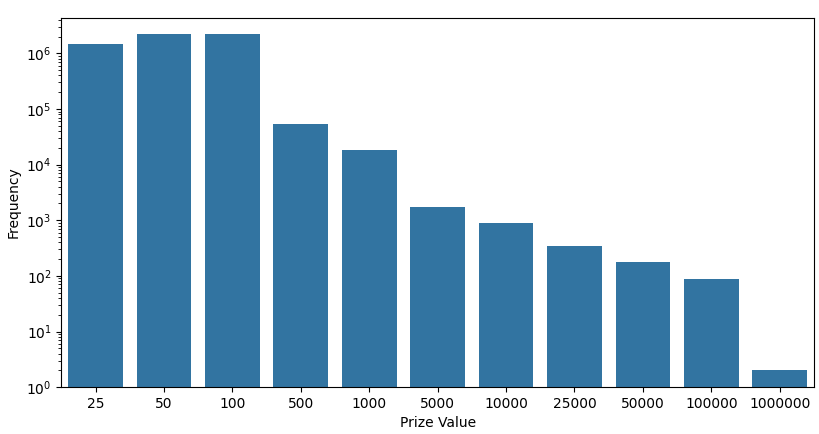
Even with a logarithmic y-axis, there is considerable skew. This can be calculated using the skew function from scipy.
from scipy.stats import skew
skewness = skew(df['Frequency'])
print(f"Skewness: {skewness:.2f}")
The result is 1.14, indicating a significant right tail in the distribution.
When performing the Monte Carlo simulations, it will be useful to have a constant containing the available prizes. This allows a winning bond to be assigned a prize at random without replacement, consistent with the actual draw mechanics. We can use the np.repeat function to generate this as an ndarray, which can be cast to a 32-bit integer type to save memory, given that we'll be working with large numbers (sys.getsizeof PRIZES itself is 22.6 MB).
import numpy as np
PRIZES = np.repeat(
tuple(PRIZE_MATRIX.keys()), tuple(PRIZE_MATRIX.values())
).astype(np.int32)
At this stage, it's interesting to note that the np.mean(PRIZES) is £77, while the np.median(PRIZES) is £50.
Now that we have our pool of prizes set up, we can move on to consider how to simulate a prize draw using random functions. This can be broken down into two parts: determining which bonds within a holding have won a prize, and randomly assigning prizes from the prize pool.
Determining winning bonds
NS&I limits the maximum number of bonds an individual can hold to 50,000. This means a couple could have a total of 100,000 bonds between them, making this a sensible maximum for the simulation. By recording the number of each winning bond, we can use this maximum dataset for smaller holdings by filtering based on bond number. We need to generate 100,000 random numbers to determine which of the 100,000 bonds has won a prize in each simulation. Performing a large number of simulations for each prize draw is necessary to get a representative dataset, so choosing an efficient approach is important. Here are several ways to approach this in Python.
Using the
random.randintfunction with a for loop or list comprehensionMethod_1: Loop over each bond and use
random.randintto check if it equals 1 to signify a winnerMethod_2: Use a list comprehension to achieve the same as above
Using the
numpy.random.randintfunction- Method_3: Create an array of n random integers, then use
np.whereto return the index of each bond that meets the winning condition. This leveragesnp.wherecalling thenp.nonzerofunction when only a condition is provided.
- Method_3: Create an array of n random integers, then use
Using a
numpy.randomgenerator object- Method_4: Pre-compute a set of choices for the generator to select from with replacement. Then, construct the array and filter it in the same way as Method_3.
import timeit
import random
import numpy as np
def method_1(n):
""" random.randint for loop """
winners = []
for i in range(n):
outcome = random.randint(1, 21000)
if outcome == 1:
winners.append(i)
return winners
def method_2(n):
""" random.randint list comprehension """
outcomes = [random.randint(1, 21_000) for _ in range(n)]
winners = [n for n, outcome in enumerate(outcomes) if outcome == 1]
return winners
def method_3(n):
""" numpy.random.randint """
outcomes = np.random.randint(0, 21_000, n) # High value is exclusive
winners = np.where(outcomes == 1)[0]
return winners
WIN_CHOICES = np.arange(21_000).astype(np.int16)
RNG = np.random.default_rng()
def method_4(n)
""" numpy.random generator with precomputed arange of choices """
outcomes = RNG.choice(WIN_CHOICES, size=n)
winners = np.where(outcomes == 0)[0]
n = 100_000
times = {}
for method in [method_1, method_2]:
time = timeit.timeit(lambda: method(n), number=100)
times[method.__name__] = time
for method_name, time in times.items():
print(f"{method_name}: {time:.2f} seconds")
Output:
method_1: 3.26 secondsmethod_2: 3.52 secondsmethod_3: 0.09 secondsmethod_4: 0.03 seconds
There is a 100-fold time saving when using the fourth approach. This will be crucial when we increase the number of iterations from 100 to hundreds of thousands or millions to generate enough data to measure returns over long periods.
Selecting prizes
We can use a similar approach to assign a prize to each winning bond. In this case, we need to perform the RNG.choices function without replacement, since each prize can only be won once per draw. The code is therefore as follows:
prizes = RNG.choice(PRIZES, replace=False, size=len(winners))
Putting it all together
Having selected methods to determine winning bonds in a draw and assign prizes to them, we can create a function to simulate a single prize draw.
import numpy as np
PRIZE_MATRIX = {
25: 1_475_218, 50: 2_190_094, 100: 2_190_094,
500: 54_807, 1_000: 18_269, 5_000: 1_747, 10_000: 874,
25_000: 350, 50_000: 175, 100_000: 87, 1_000_000: 2
}
PRIZES: np.ndarray = np.repeat(
tuple(PRIZE_MATRIX.keys()), tuple(PRIZE_MATRIX.values())
).astype(np.int32)
WINNING_ODDS = 21_000
WIN_CHOICES: np.ndarray = np.arange(WINNING_ODDS).astype(np.int16)
RNG: np.random._generator.Generator = np.random.default_rng()
def prize_draw(holding_size: int) -> list[tuple[int, int]]:
""" Simulate single prize draw with holding_size bonds
returns list of winning (bond, prize) """
# Check each bond for winning condition (value = 0)
outcomes: np.ndarray = RNG.choice(WIN_CHOICES, size=holding_size)
winners: np.ndarray = np.where(outcomes == 0)[0]
# Randomly sample prizes (without replacement) for each winner
prizes: np.ndarray = RNG.choice(
PRIZES, replace=False, size=len(winners))
# Return list of winning bonds and assigned prizes
return list(zip(winners.astype(np.int32), prizes))
Conclusion
We've created a custom function to simulate a Premium Bond prize draw. It offers a clear and efficient way to determine winning bonds and their corresponding prizes. By using numpy's random generator, we ensure a fair and efficient selection process. This method provides a scalable solution that can be applied to various holding sizes and periods.
In the next instalment, we'll explore using the prize_draw function in a Monte Carlo experiment with multiple simulations over different holding periods. Parallel processing will be a key efficiency booster, and we'll need to save the valuable data we generate to disk. Later, we'll analyse this data to understand the distribution of outcomes in various scenarios.
Subscribe to my newsletter
Read articles from Jason Shiers directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
