Understanding and Calculating Cosine Similarity

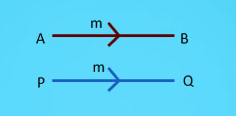
This article is a continuation from the previous article where we explored the mathematical foundation of dot product and cosine similarity and calculated the values for cos(θ) and θ of a two dimensional vector using cosine similarity.

$$A = 3i + 5j \;\; \text{and } \; B = 4i +8j$$

The values obtained from the calculation for cos(θ) and θ were 0.9970 and 4.4° respectively.

In this article we would dive into understanding the different classifications of cosine similarities and practical implementation of them.

It is important to understand that similarity is measured between a value of +1 and -1.Smaller angles between the vectors results in larger cosine values. In the example of the previous article an angle of 4.4° resulted in a cosine value of less than 1.

Similar Vectors

Similar vectors are vectors that have the same direction (they are parallel) but may differ in magnitude. The value of θ between the vectors is close O and the cos(θ) is close to 1.The following schematic represents an Similar vector.

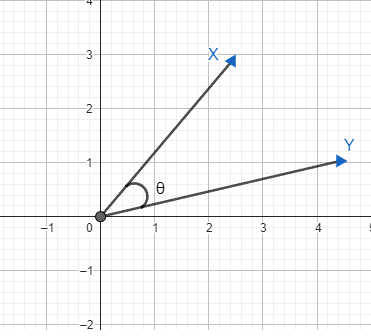
Lets take an example of a Similar vector and see how to check if a given vector is classifies as a similar vector.

Consider the following three dimensional vector

$$A=4i +1j-3k\;\text{and}\;B=8i+2j-6k$$

To verify if these vectors are similar , it is necessary to check if B is a positive scalar multiple of A i.e.

$$B=kA$$

To find k

$$8i+2j-6k=k(4i +1j-3k)$$

Comparing the elements of the vector we get

$$B_i=2A_i\;\text{i.e}\;8=2*4$$

$$B_j=2A_j\;\text{i.e}\;2=2*1$$

$$B_k=2A_k\;\text{i.e}\;6=2*3$$

So B is a positive scalar multiple of A and hence the vectors are similar (i.e., they point in the same direction).

Lets calculate the angle between them to reconfirm if they are indeed similar using the cosine formula

$$cos(θ)= \frac{∣A∣∣B∣}{A⋅B} ​$$

The dot product of the vectors is

$$​A⋅B=(2)(4)+(3)(6)+(−1)(−2)$$

$$A⋅B=8+18+2=28$$

while its magnitude is

$$∣A∣= \sqrt{ (2)^2 +(3) ^2 +(−1)^2 } = \sqrt{4+9+1} ​ = \sqrt{14}$$

$$∣ 𝐵 ∣ = \sqrt{( 4 ) ^2 + ( 6 ) ^2 + ( − 2 ) ^ 2} = \sqrt{16+36+4} = \sqrt{56}$$

value of cos(θ) is

$$cos(θ)= \frac{28}{\sqrt{14 * 56}}=1$$

and value of θ is

$$θ=cos −1 (1)=0^∘$$

Given that the value cos(θ) is 1 and value of θ is O, this reconfirms that the vector is indeed a similar vector.

Orthogonal Vectors

Orthogonal vectors are vectors where the angle between the vectors is almost 90° and value of cos(θ) is O and the dot product of every pair of the vector is O which corresponds to an angle of exactly 90° between them.

The following diagram represents an Orthogonal vector.

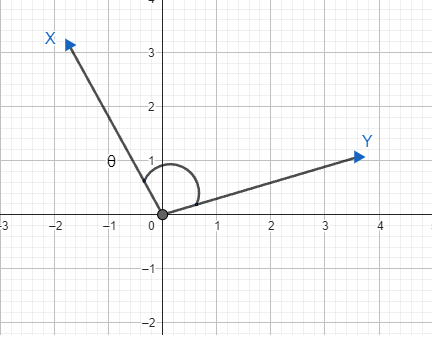
Lets consider a three dimensional vector

$$A=i+2j+3k\;\text{and}\;B=4i+5j−\frac{14}{3}k$$

The value of the dot product is

$$A⋅B=1×4+2×5+3×(− \frac{14}3 ​ )$$

$$A⋅B=4+10−14=0$$

The dot product of the vector is O. Lets reconfirm it by calculating its cos(θ) and the 0 value.

The magnitude of A is

$$∣A∣= \sqrt{(1)^2 +(2)^2 +(3)^2}=\sqrt{14}$$

and magnitude of B is

$$∣B∣= \sqrt{ (4)^ 2 +(5)^ 2 +(− \frac{14}{3} ​ )^2}=\frac{\sqrt{565}}{3}$$

Calculate cos(θ)

$$cos(θ)= \frac{A⋅B}{∣A∣∣B∣} = \frac{0}{\sqrt{14 * \frac{565}{3}}} ​ =0$$

​ and the angle θ between the two vectors is

$$θ=cos^{−1} (0)=90^∘$$

This reconfirms that the vector is an orthogonal vector.

Opposite Vectors

Opposite vectors are vector types that have the same magnitude but the directions are opposite and the angle 0 between the vectors is close to 180° and value ofcos(θ) is close to -1

The following diagram represents an opposite vector.

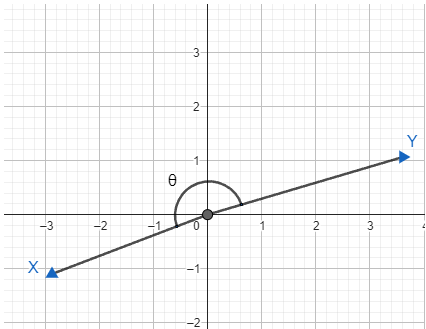
Consider the following vector

$$A=3i+4j−5k\;\;\text{and }\; B=−3i−4j+5k$$

To confirm if these are vectors are opposite vectors we have to check if B=-A.

$$B=−1×(3i+4j−5k)=−3i−4j+5k$$

Since B is negative of A its safe to say that A and B are opposite vectors.

To reconfirm it we can calculate the value of θ and cos(θ)

The value of the dot product is

$$A⋅B=(7)(−7)+(−2)(2)+(4)(−4)$$

$$A⋅B=−49−4−16=−69$$

and the magnitude of A is

$$∣A∣= \sqrt{(7)^2 +(−2)^2 +(4)^2} ​ = 49+4+16 ​ = 69 ​$$

and the magnitude of B is

$$∣B∣= \sqrt{ (−7) 2 +(2) 2 +(−4) 2} ​ = 49+4+16 ​ = 69$$

Calculate cos(θ)

$$cos(θ)= \frac{A⋅B}{∣A∣∣B∣} = \frac{-69}{\sqrt{69} *\sqrt{69} } ​ =-1$$

​ and the angle θ between the two vectors is

$$θ=cos −1 (−1)=180^∘$$

The vectors have have an angle of 180° between them and cos(θ) is -1.This confirms that the vectors are indeed opposite vectors.

Lets Test

We will use a python script to test the cosine similarity. The vectors are the same vectors that were used to manually compute the cosine similarity in the previous article.The calculated value was 0.99.

import numpy as np

#numpy arrays
v1 = np.array((3,5))
v2 = np.array((4,8))

dot_product = np.dot(v1, v2)

x_magnitude = np.sqrt(np.sum(v1**2)) 
y_magnitude = np.sqrt(np.sum(v2**2))

cos_similarity = dot_product / (x_magnitude * y_magnitude)

print(cos_similarity)

the output is

We could also use the Scikit-learn’s inbuilt cosine_similarity function

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity

A = np.array([[3, 5]])
B = np.array([[4, 8]])

cos_similarity = cosine_similarity(A, B)
print(cos_similarity)

The output is similar to the previous output

Lets test it on some phrases. The phrases used below are the same phrases that was used in this article to calculate the Euclidean distance between the vectors.

import numpy as np

def ret_cos_similarity(v1, v2):

    dot_product = np.dot(v1, v2)
    x_magnitude = np.sqrt(np.sum(v1**2)) 
    y_magnitude = np.sqrt(np.sum(v2**2))

    cos_similarity = dot_product / (x_magnitude * y_magnitude)
 return cos_similarity


corpus = [ 'Paris is capital of France',
           'Boeing and Airbus are two companies that build aircrafts',
           'Rome is capital of Italy'  ]

from sklearn.feature_extraction.text import CountVectorizer

V = CountVectorizer().fit_transform(corpus).toarray()

v1=(V[0, :])
v2=(V[1, :])
v3=(V[2, :])

print('Similarity between: ')
print('\tPhrase 1 and Phrase 2: ',ret_cos_similarity(v1,v2))
print('\tPhrase 2 and Phrase 3: ', ret_cos_similarity(v2,v3))
print('\tPhrase 1 and Phrase 3: ', ret_cos_similarity(v1,v3))

I created a custom cosine similarity function ret_cos_similarity

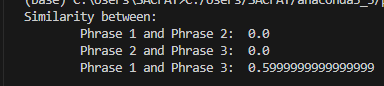
As expected Phrase1 and Phrase2 & Phrase2 and Phrase3 are orthogonal vectors given the calculated value of cos(θ) is O while Phrase1 and Phrase3 are similar vectors as the value of cos(θ) is closer to 1.

You could also use Scikit-learn’s inbuilt cosine_similarity function

import numpy as np
from scipy.spatial import distance
from sklearn.metrics.pairwise import cosine_similarity

corpus = [ 'Paris is capital of France',
           'Boeing and Airbus are two companies that build aircrafts',
           'Rome is capital of Italy'  ]

from sklearn.feature_extraction.text import CountVectorizer

V = CountVectorizer().fit_transform(corpus).toarray()

v1=(V[0, :] )
v2=(V[1, :] )
v3=(V[2, :] )


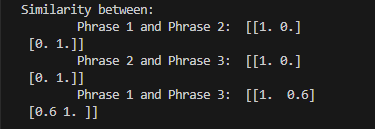
print('Similarity between: ')
print('\tPhrase 1 and Phrase 2: ',cosine_similarity((v1,v2)))
print('\tPhrase 2 and Phrase 3: ', cosine_similarity((v2,v3)))
print('\tPhrase 1 and Phrase 3: ', cosine_similarity((v1,v3)))

The output is in form of a matrix which isnt that intuitive.

Closing Notes

Cosine similarity is a powerful and widely-used metric for measuring the similarity between vectors in high-dimensional spaces. It is one of the most widely used metric for vector analysis. Hope this article has helped to provide some insights into the mathematical intricacies of cosine similarity and its practical usage.

Thank you for reading !!!