Mastering the Two-Pointer Technique in Java: A Detailed Guide

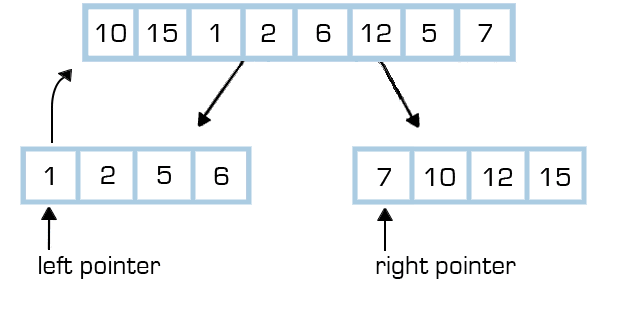
What is the Two-Pointer Technique?

The two-pointer technique is a pattern often used in scenarios where you need to search for pairs in a sequence or compare elements in a sorted array or list. As the name suggests, it involves using two pointers, typically initialized at different positions, which traverse the data structure according to specific conditions.

When to Use the Two-Pointer Technique?

This technique is most useful in problems like:

• Finding pairs in a sorted array that sum up to a target value.

• Removing duplicates from a sorted array.

• Merging two sorted arrays.

• 

  Solving problems related to palindromes or detecting subarrays with specific properties.

• Finding the maximum area of water that can be contained between lines (Container with Most Water problem).

• Partitioning arrays based on certain conditions.

Example 1: Finding a Pair with a Given Sum

Let's start with a classic problem where the two-pointer method shines: finding a pair of numbers in a sorted array that add up to a given sum.

Problem Statement:

Given a sorted array of integers and a target sum, find the pair of numbers in the array that add up to the target.

Approach:

1. Initialization: Set one pointer at the beginning (left) and the other at the end (right) of the array.

2. Iteration:

   • If the sum of the elements at the two pointers equals the target, return the pair.

   • If the sum is less than the target, move the left pointer to the right to increase the sum.

   • If the sum is greater than the target, move the right pointer to the left to decrease the sum.

3. Termination: The loop continues until the pointers meet.

Java Implementation:

public class TwoPointerExample {
    public static int[] findPairWithSum(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left < right) {
            int sum = nums[left] + nums[right];

            if (sum == target) {
                return new int[]{nums[left], nums[right]};
            } else if (sum < target) {
                left++;
            } else {
                right--;
            }
        }
        return new int[]{-1, -1}; // Return -1 if no pair is found
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 6, 8, 10};
        int target = 10;

        int[] result = findPairWithSum(nums, target);

        if (result[0] != -1) {
            System.out.println("Pair found: " + result[0] + ", " + result[1]);
        } else {
            System.out.println("No pair found with the given sum.");
        }
    }
}

Output:

Pair found: 2, 8

Example 2: Removing Duplicates from a Sorted Array

Another common application of the two-pointer technique is removing duplicates from a sorted array in-place.

Problem Statement:

Given a sorted array nums, remove the duplicates in-place such that each element appears only once and returns the new length.

Approach:

1. Initialization: Use two pointers, i (slow-runner) and j (fast-runner). Start both at the beginning of the array.

2. Iteration:

   • Move j forward and compare nums[j] with nums[i].

   • If they are different, increment i and assign nums[j] to nums[i].

3. Termination: The array up to index i will have no duplicates.

Java Implementation:

public class RemoveDuplicates {
    public static int removeDuplicates(int[] nums) {
        if (nums.length == 0) return 0;

        int i = 0; // Pointer for the position of the last unique element

        for (int j = 1; j < nums.length; j++) {
            if (nums[j] != nums[i]) {
                i++;
                nums[i] = nums[j];
            }
        }

        return i + 1; // Length of array without duplicates
    }

    public static void main(String[] args) {
        int[] nums = {1, 1, 2, 3, 3, 4, 4, 5};
        int newLength = removeDuplicates(nums);

        System.out.print("Array after removing duplicates: ");
        for (int k = 0; k < newLength; k++) {
            System.out.print(nums[k] + " ");
        }
    }
}

Output:

Array after removing duplicates: 1 2 3 4 5

Example 3: Merging Two Sorted Arrays

The two-pointer technique is ideal for merging two sorted arrays into one sorted array efficiently.

Problem Statement:

Given two sorted arrays arr1 and arr2, merge them into a single sorted array.

Approach:

1. Initialization: Use two pointers, i for arr1 and j for arr2.

2. Iteration:

   • Compare the elements at arr1[i] and arr2[j].

   • Add the smaller element to the merged array and move the corresponding pointer.

3. Termination: Once one array is exhausted, append the remaining elements of the other array.

Java Implementation:

import java.util.Arrays;

public class MergeSortedArrays {
    public static int[] mergeArrays(int[] arr1, int[] arr2) {
        int[] merged = new int[arr1.length + arr2.length];
        int i = 0, j = 0, k = 0;

        // Merge until one array is exhausted
        while (i < arr1.length && j < arr2.length) {
            if (arr1[i] < arr2[j]) {
                merged[k++] = arr1[i++];
            } else {
                merged[k++] = arr2[j++];
            }
        }

        // Append remaining elements
        while (i < arr1.length) {
            merged[k++] = arr1[i++];
        }

        while (j < arr2.length) {
            merged[k++] = arr2[j++];
        }

        return merged;
    }

    public static void main(String[] args) {
        int[] arr1 = {1, 3, 5, 7};
        int[] arr2 = {2, 4, 6, 8, 10};

        int[] merged = mergeArrays(arr1, arr2);
        System.out.println("Merged Array: " + Arrays.toString(merged));
    }
}

Output:

Merged Array: [1, 2, 3, 4, 5, 6, 7, 8, 10]

Example 4: Container With Most Water

This problem involves finding two lines that together with the x-axis form a container, such that the container contains the most water.

Problem Statement:

Given an array height where each element represents the height of a vertical line at that index, find two lines that together with the x-axis form a container that holds the most water.

Approach:

1. Initialization: Use two pointers, left at the start and right at the end of the array.

2. Iteration:

   • Calculate the area formed by the lines at left and right.

   • Move the pointer pointing to the shorter line inward to potentially find a larger area.

3. Termination: Continue until the pointers meet.

Java Implementation:

public class ContainerWithMostWater {
    public static int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int maxArea = 0;

        while (left < right) {
            // Calculate the area
            int width = right - left;
            int minHeight = Math.min(height[left], height[right]);
            int currentArea = width * minHeight;

            // Update max area if needed
            maxArea = Math.max(maxArea, currentArea);

            // Move the pointer pointing to the shorter line
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return maxArea;
    }

    public static void main(String[] args) {
        int[] height = {1,8,6,2,5,4,8,3,7};
        System.out.println("Maximum area: " + maxArea(height));
    }
}

Output:

Maximum area: 49

Example 5: Palindrome Checking

Using the two-pointer technique, you can efficiently check if a given string is a palindrome.

Problem Statement:

Determine whether a given string is a palindrome, considering only alphanumeric characters and ignoring cases.

Approach:

1. Initialization: Use two pointers, left at the start and right at the end of the string.

2. Iteration:

   • Move left forward and right backward until alphanumeric characters are found.

   • Compare the characters at left and right.

   • If they don't match, the string is not a palindrome.

3. Termination: If all corresponding characters match, the string is a palindrome.

Java Implementation:

public class PalindromeChecker {
    public static boolean isPalindrome(String s) {
        int left = 0, right = s.length() - 1;

        while (left < right) {
            // Move left pointer to the next alphanumeric character
            while (left < right && !Character.isLetterOrDigit(s.charAt(left))) {
                left++;
            }

            // Move right pointer to the previous alphanumeric character
            while (left < right && !Character.isLetterOrDigit(s.charAt(right))) {
                right--;
            }

            // Compare characters
            if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) {
                return false;
            }

            left++;
            right--;
        }

        return true;
    }

    public static void main(String[] args) {
        String s1 = "A man, a plan, a canal: Panama";
        String s2 = "race a car";

        System.out.println("\"" + s1 + "\" is a palindrome? " + isPalindrome(s1));
        System.out.println("\"" + s2 + "\" is a palindrome? " + isPalindrome(s2));
    }
}

Output:

"A man, a plan, a canal: Panama" is a palindrome? true
"race a car" is a palindrome? false

Example 6: Partitioning Arrays (Dutch National Flag Problem)

This problem involves rearranging elements in an array based on a pivot value using the two-pointer approach.

Problem Statement:

Given an array containing only 0s, 1s, and 2s, sort the array in-place so that all 0s come first, followed by 1s, then 2s.

Approach:

1. Initialization: Use three pointers:

   • low for the next position of 0.

   • mid for current element.

   • high for the next position of 2.

2. Iteration:

   • If the current element is 0, swap it with low and move both low and mid pointers forward.

   • If the current element is 1, move the mid pointer forward.

   • If the current element is 2, swap it with high and move the high pointer backward.

3. Termination: Continue until mid exceeds high.

Java Implementation:

public class DutchNationalFlag {
    public static void sortColors(int[] nums) {
        int low = 0, mid = 0, high = nums.length - 1;

        while (mid <= high) {
            switch (nums[mid]) {
                case 0:
                    swap(nums, low, mid);
                    low++;
                    mid++;
                    break;
                case 1:
                    mid++;
                    break;
                case 2:
                    swap(nums, mid, high);
                    high--;
                    break;
            }
        }
    }

    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public static void main(String[] args) {
        int[] colors = {2, 0, 2, 1, 1, 0};
        sortColors(colors);
        System.out.print("Sorted array: ");
        for (int color : colors) {
            System.out.print(color + " ");
        }
    }
}

Output:

Sorted array: 0 0 1 1 2 2

Why the Two-Pointer Technique is Efficient

The efficiency of the two-pointer technique lies in its ability to reduce the time complexity. In the above examples:

• Finding a Pair with a Given Sum: Reduced from O(n²) to O(n).

• Removing Duplicates: Achieved in O(n) time and O(1) space.

• Merging Two Sorted Arrays: Performed in O(n + m) time, where n and m are the lengths of the arrays.

• Container With Most Water: Solved in O(n) time.

• Palindrome Checking: Done in O(n) time.

• Dutch National Flag Problem: Sorted in O(n) time with a single pass.

This makes the two-pointer technique particularly useful in scenarios where performance is crucial, such as processing large datasets or in real-time applications.

Other Applications of the Two-Pointer Technique

• Finding Subarrays with Specific Properties: Such as finding the smallest subarray with a given sum.

• Sliding Window Problems: Where you need to find a window that satisfies certain conditions.

• Intersection of Two Arrays: Finding common elements between two arrays.

• Three-Sum and Four-Sum Problems: Extending the two-pointer approach for more complex scenarios.

Conclusion

The two-pointer technique is a powerful tool in your algorithmic arsenal. By mastering it, you can tackle a wide range of problems more efficiently. Whether you are preparing for coding interviews or just want to enhance your problem-solving skills, understanding and applying this method is a must. Practice with various problems to get comfortable with different scenarios where the two-pointer technique can be applied.