Mastering the Sliding Window Technique in Problem Solving

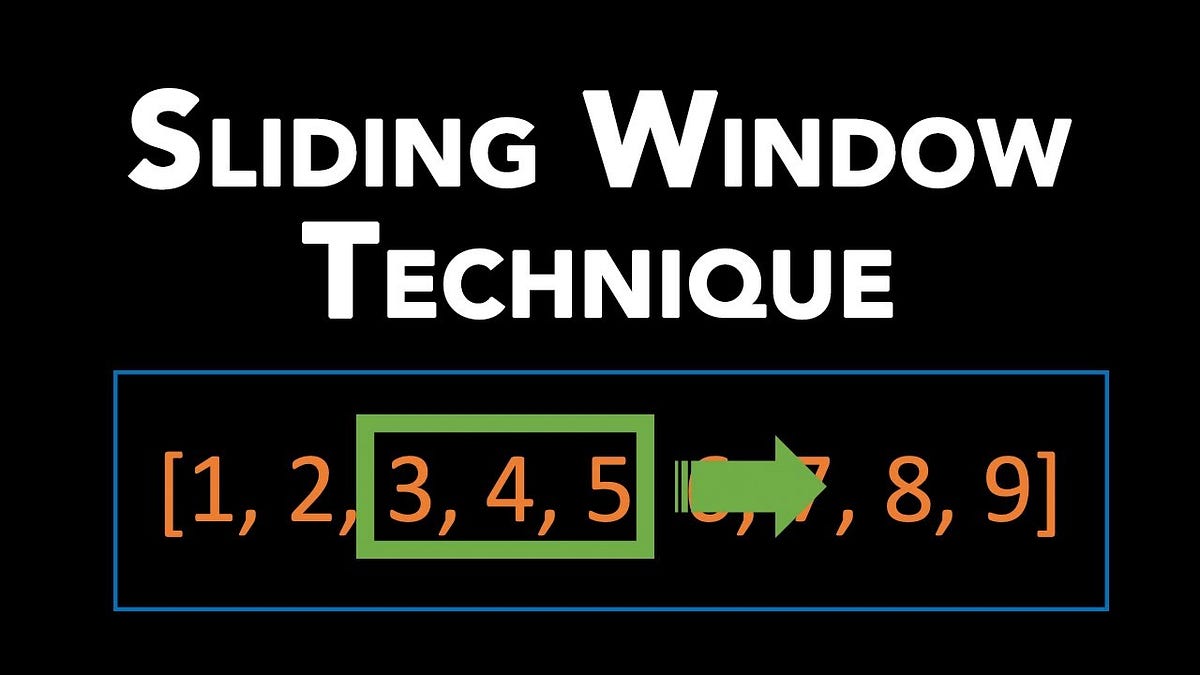
The sliding window method is a powerful technique that helps in optimizing solutions for a variety of problems, particularly those involving arrays or sequences. This approach is often more efficient than traditional methods like nested loops, making it a must-know for anyone looking to improve their problem-solving skills.

What is the Sliding Window Technique?

The sliding window technique is used to solve problems where you need to consider a subset of data that "slides" across the entire dataset. This subset, or "window," can be fixed or variable in size, depending on the problem requirements.

Examples of Sliding Window Technique

1. Fixed-Length Sliding Window

In a fixed length sliding window, the size of the window remains constant as it slides across the data. This approach is often used in problems where you need to find the maximum, minimum, or sum of elements within a subarray of a given length.

Example 1: Maximum Sum of k Consecutive Elements

Problem: Find the maximum sum of k consecutive elements in an array.

Solution:

1. Start by calculating the sum of the first k elements.

2. Then slide the window one element at a time, subtracting the element that goes out of the window and adding the one that comes into the window.

3. Keep track of the maximum sum encountered during this process.

Java Implementation:

public int maxSum(int[] nums, int k) {
    int maxSum = 0, windowSum = 0;

    for (int i = 0; i < k; i++) {
        windowSum += nums[i];
    }

    maxSum = windowSum;

    for (int i = k; i < nums.length; i++) {
        windowSum += nums[i] - nums[i - k];
        maxSum = Math.max(maxSum, windowSum);
    }

    return maxSum;
}

Example 2: Maximum Number of Vowels in a Substring

Problem: Given a string s and an integer k, find the maximum number of vowels in any substring of length k.

Solution:

1. Initialize a count of vowels for the first k characters.

2. Slide the window across the string, updating the count by adding the vowel count of the new character and subtracting the vowel count of the character that exits the window.

3. Track the maximum count of vowels.

Java Implementation:

public int maxVowels(String s, int k) {
    int maxVowels = 0, currentVowels = 0;

    for (int i = 0; i < k; i++) {
        if (isVowel(s.charAt(i))) {
            currentVowels++;
        }
    }

    maxVowels = currentVowels;

    for (int i = k; i < s.length(); i++) {
        if (isVowel(s.charAt(i))) {
            currentVowels++;
        }
        if (isVowel(s.charAt(i - k))) {
            currentVowels--;
        }
        maxVowels = Math.max(maxVowels, currentVowels);
    }

    return maxVowels;
}

private boolean isVowel(char c) {
    return "aeiouAEIOU".indexOf(c) != -1;
}

2. Variable-Length Sliding Window

In a variable-length sliding window, the size of the window can change as it slides, based on the conditions of the problem. This approach is useful in problems where you need to find the smallest or largest subarray that meets a certain condition.

Example 3: Smallest Subarray with a Given Sum

Problem: Find the smallest subarray with a sum greater than or equal to a given value.

Solution:

1. Start with an empty window and expand it by adding elements until the sum exceeds the given value.

2. Once the condition is met, try to shrink the window from the left to find the minimum length that still satisfies the condition.

3. Keep track of the minimum window size found.

Java Implementation:

public int minSubArrayLen(int target, int[] nums) {
    int minLength = Integer.MAX_VALUE;
    int left = 0, windowSum = 0;

    for (int right = 0; right < nums.length; right++) {
        windowSum += nums[right];

        while (windowSum >= target) {
            minLength = Math.min(minLength, right - left + 1);
            windowSum -= nums[left];
            left++;
        }
    }

    return (minLength == Integer.MAX_VALUE) ? 0 : minLength;
}

Example 4: Longest Substring Without Repeating Characters

Problem: Given a string s, find the length of the longest substring without repeating characters.

Solution:

1. Use a sliding window to expand the substring by adding characters to the window.

2. If a character repeats, shrink the window from the left until the character is no longer in the window.

3. Track the maximum length of the substring encountered.

Java Implementation:

public int lengthOfLongestSubstring(String s) {
    int[] charIndex = new int[128];
    int maxLength = 0;
    int left = 0;

    for (int right = 0; right < s.length(); right++) {
        char c = s.charAt(right);
        left = Math.max(charIndex[c], left);
        maxLength = Math.max(maxLength, right - left + 1);
        charIndex[c] = right + 1;
    }

    return maxLength;
}

Common Use Cases

• Maximum or Minimum Sum Subarray: Problems where you need to find the maximum or minimum sum within a subarray.

• Substring Problems: When dealing with problems related to substrings or subarrays where certain conditions need to be met.

• Finding Unique Elements: Problems that require finding the maximum number of unique elements within a subarray of a given length.

Why Sliding Window is Efficient

The sliding window technique reduces the time complexity of problems that would otherwise require nested loops. Instead of recalculating the sum or condition for each subarray, the sliding window efficiently updates the result as it moves across the array, leading to significant performance improvements.

Conclusion

Mastering the sliding window technique can be a game-changer in your problem-solving toolkit. It not only simplifies complex problems but also provides an optimal solution in terms of time complexity. The key is to identify whether a problem can be approached using this technique and then implement it effectively.

---

By understanding and applying the sliding window technique, you can tackle a wide range of problems more efficiently. Give it a try on your next coding challenge, and you'll likely see the benefits immediately.

Feel free to share your thoughts and any questions you have in the comments below! Happy coding!