Part 4: a First Run Attempt
 Greg Alt
Greg Alt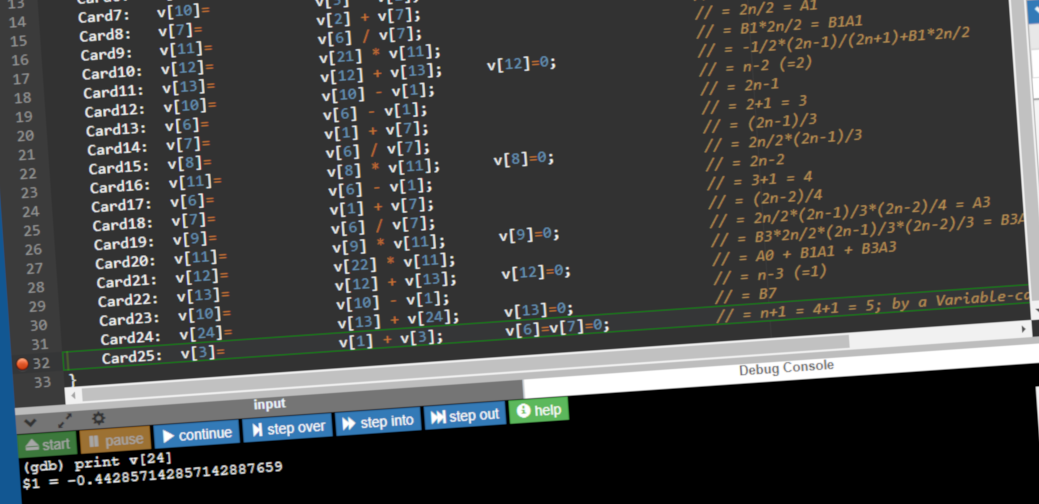
This is the fourth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program
In the previous blog post, I gave some background on what it has meant to run a program across three different eras, the 1840s, the 1940s, and the modern era since the 1950s.
That leads to a question: how exactly am I going to run Lovelace's program?
How am I going to run this program?
Running on a physical Analytical Engine is out of the question at the moment, as none yet exist. There is an effort to build one, but without Babbage leaving a clear and definitive single set of plans, it has not been an easy task.
Even when this is built, though, it’s not clear that Ada Lovelace’s program could run on it. I’ll talk about this more, but she found it necessary to extend the design of the Engine to support an auto-increment indexing variable card, something Babbage suggested was possible but never fully specified.
Emulators?
The next option, more promising, would be to manually convert the table into a machine language of virtual cards and then load these into one of several Analytical Engine emulators. I know of a few, and others might exist
Enigmatic Code's Analytical Engine Emulator in Python—this last one is especially interesting because the author built it specifically to run Lovelace's program from Note G. As such it added support for auto-increment indexing, an essential feature of the virtual machine that Lovelace coded for.
My understanding is that aside from the Python emulator, the last one in the list, these were created based on Babbage’s known design, so they suffer the downside of not supporting auto-increment indexing, and are therefore unable to run the program as originally intended by the programmer.
It is a reasonable, principled direction to take, staying true to Babbage’s design without embellishments, but it creates a problem when Lovelace herself seems to have relied on one such embellishment in her program. This highlights a key point, that the virtual machine embodied in Babbage's explicit designs is distinct from the virtual machine that Lovelace programmed for.
For this reason, my general feeling about emulators is that they are primarily a tool for studying the hardware (or virtual hardware design) they emulate. In this, they are a fascinating and essential tool. However, they are not the best choice for my project.
For my goal of studying the program itself, I already have a set of tools for running, debugging, and understanding code, and adding the complexity of an emulator to the process pushes me farther away from the code itself.
My Choice: Transliteration to C
That leaves my final choice, convert the program to a modern programming language, and then compile and run that using modern tools I’m familiar with.
Others have gone this route before, and I’m greatly indebted to them for what I learned exploring their conversions. This route, though, is not free of tradeoffs, and people are forced to choose based on their goals.
First is a Two-Bit History's What Did Ada Lovelace's Program Actually Do? This is an excellent introduction to the program, giving a good background on the Bernoulli Number math as well. I'll talk more about the distinction in my next post, but they present a translation of Lovelace's program to C. Presenting the code with modern embellishments like "while (v6 > 2 * v3 - (2 * (v3 - v10) - 2))" is fine for the goal of understanding what the program does, but for my purposes it creates too much distance from the original code.
I especially appreciated their calling out of the v4/v5 typo and also highlighting how Lovelace differed from Menabrea's views on the complexity of programming itself, that vast endeavor that lives between abstract math and physical complexities of computer hardware:
Lovelace also grasped that “the making of the cards” would not be a mere afterthought and that it could be done well or done poorly. This is hard to appreciate without understanding her program from Note G and seeing for oneself the care she put into designing it.
Another source I found especially valuable was Enigmatic Code's blog series, "Running the first program" I've mentioned their Python emulator, but they also presented a couple different implementations of Lovelace's program directly in Python. First, they presented a more modern translation into Python, using Fraction rational numbers. This is another good starting point for understanding what the program does. The second Python implementation was especially interesting—it presented a much more faithful transliteration.
Honestly, I probably could have saved myself some time if I had more closely studied this second version. Instead, I started out on my journey, looking to make a more direct and dumber transliteration, and only later read through the rest of the blog. I find it interesting in looking back at their Python code, I see that we encountered similar problems and addressed them in much the same way. I feel that my coming to the same conclusions serves as an independent confirmation of their results.
Their key results are:
Using auto-increment as Lovelace intended, in a simple and elegant way
Finding and fixing a negation bug in operation 24, among others.
Implementing an outer loop to match the expected physical loop of cards
Transliterating the original code
Successfully running “indefinitely from the very beginning”
Though I came to many of the same conclusions, my preferred route was to transliterate to C instead of Python, for a few reasons. It is a ubiquitous language, with mature tools to compile, run, and debug on nearly every modern platform. It is low-level, still allowing goto statements, which allows a level of flow control comparable to assembly language. Importantly, the structure of C allows for the very dumb, mechanical transliteration I am aiming for. And, lastly, it is a language I’m very familiar with.
As a starting point, I made a digital transcription of Lovelace’s original table. I kept it as much as possible identical to the original, just in more machine-readable text. I chose a spreadsheet for this, as spreadsheets are a modern digital evolution of paper spreadsheets used before the 1970s. Excel and Google Sheets both also support basic string substitution operations, which should suffice for a very dumb transliteration of the transcribed table. To better share the transliteration process, I ported these spreadsheet formulas to a simple Python script. I will share this in a later blog post.
All that remains is some very minimal C boiler-plate and the table can be compiled and run as C code. This will be my starting point.
A Transcribed, Digital Table
Here’s a transcription of the table I showed in a previous post, as a Google Sheets spreadsheet. This is transcribed as-is, staying as true to the published table as possible, with no attempt to correct known typos in the original: TranscribedNoteG-NoCorrections
A Trivial Transliteration
After transcribing the table, I did a trivial, automated transliteration of the first six columns of the numbered rows in the table. This doesn’t yet handle conditional branches. The result is this fairly straightforward, legal C code. At the top is some simple C boilerplate and definitions for the variables listed at the top of the table.
int main() { long double v[100] = { 0 };
v[1]= 1; // [1]
v[2]= 2; // [2]
v[3]= 4; // [n]
v[21] = 1.0/6.0; // [B1]
v[22] = -1.0/30.0; // [B3]
v[23] = 1.0/42.0; // [B5]
Card1: v[4]=v[5]=v[6]= v[2] * v[3]; // = 2n
Card2: v[4]= v[4] - v[1]; // = 2n-1
Card3: v[5]= v[5] + v[1]; // = 2n+1
Card4: v[11]= v[5] / v[4]; v[5]=v[4]=0; // = (2n-1)/(2n+1)
Card5: v[11]= v[11] / v[2]; // = 1/2*(2n-1)/(2n+1)
Card6: v[13]= v[13] - v[11]; v[11]=0; // = -1/2*(2n-1)/(2n+1) = A0
Card7: v[10]= v[3] - v[1]; // = n-1 (=3)
Card8: v[7]= v[2] + v[7]; // = 2+0 = 2
Card9: v[11]= v[6] / v[7]; // = 2n/2 = A1
Card10: v[12]= v[21] * v[11]; // = B1*2n/2 = B1A1
Card11: v[13]= v[12] + v[13]; v[12]=0; // = -1/2*(2n-1)/(2n+1)+B1*2n/2
Card12: v[10]= v[10] - v[1]; // = n-2 (=2)
Card13: v[6]= v[6] - v[1]; // = 2n-1
Card14: v[7]= v[1] + v[7]; // = 2+1 = 3
Card15: v[8]= v[6] / v[7]; // = (2n-1)/3
Card16: v[11]= v[8] * v[11]; v[8]=0; // = 2n/2*(2n-1)/3
Card17: v[6]= v[6] - v[1]; // = 2n-2
Card18: v[7]= v[1] + v[7]; // = 3+1 = 4
Card19: v[9]= v[6] / v[7]; // = (2n-2)/4
Card20: v[11]= v[9] * v[11]; v[9]=0; // = 2n/2*(2n-1)/3*(2n-2)/4 = A3
Card21: v[12]= v[22] * v[11]; // = B3*2n/2*(2n-1)/3*(2n-2)/3 = B3A3
Card22: v[13]= v[12] + v[13]; v[12]=0; // = A0 + B1A1 + B3A3
Card23: v[10]= v[10] - v[1]; // = n-3 (=1)
Card24: v[24]= v[13] + v[24]; v[13]=0; // = B7
Card25: v[3]= v[1] + v[3]; v[6]=v[7]=0; // = n+1 = 4+1 = 5; by a Variable-card. by a Variable card.
}
That looks like something we can run! I just need to compile it and then run it in a debugger I’m familiar with.
Let’s Run It!
Everyone has their favorite tools, but there are a few online C debuggers that make this especially simple to try out. You just paste the code in and click by the line number to get a dot showing the breakpoint. Then you hit the “Debug” button and type “run” in the debug console. When the breakpoint hits, you can see all of the variables and their values on the right. Typing “c” to continue starts execution again until it ends or hits another breakpoint.
Putting a breakpoint on the Card25 line, I run and display v[24] as a watch expression. Aside from the lack of fire and steam, this is much like how an operator might run a program on an Analytical Engine and look at the variables physically displayed.
What’s the result?
-0.442857142857142887659
The table says v24 should be B7 at this point. Sadly that doesn’t look much like what I was expecting, which was:
B7 = -1/30 = -0.03333333333…
That’s ok. As any programmer will tell you, things never run flawlessly the first time. And honestly, I was especially impatient to run this code.
Time to debug…
I find debugging is easiest when I can pull up a seat next to the programmer that wrote the code, and we can go over it together. That’s not possible with this program, obviously, but Lovelace wrote extensively about this code in Note G. I’ll do my best to pair-debug some more with her to get this thing working.
In my next blog post, I'll make some progress for a better second run.
Subscribe to my newsletter
Read articles from Greg Alt directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
