What is Big-O Notation?

Big-O Notation is a mathematical concept used in computer science to describe efficiency of an algorithm in terms of its time or space complexity as the input size grows. It provides a high-level understanding of how the runtime or the space requirements of an algorithm will scale with increasing input size.

Imagine you're searching for a word in a dictionary. The time it takes you to find the word depends on how you search. Do you flip through each page one by one? Do you divide the dictionary in half and eliminate large sections with each guess? Big-O Notation helps quantify these differences in efficiency.

Why is Big-O Important?

Understanding Big-O Notation is crucial because it allows you to:

Compare Algorithms: Big-O allows you to compare the efficiency of different algorithms, helping you choose the most suitable one for your problem.
Predict Performance: It gives insight into how an algorithm will perform as the input size grows, which is crucial for developing scalable systems.
Optimize Code: Recognize inefficient code can help you make improvements, resulting in faster and more scalable software.

Key Concepts:

Time Complexity: Refers to how the running time of an algorithm increases as the size of the input increases.
Space Complexity: Refers to how the memory usage of an algorithm increases with the size of the input.

Types of Complexities: A Breakdown

Let's explore some common types of complexities you'll encounter:

O(1): Constant time - The algorithm takes the same amount of time regardless of the input size.

Example: Accessing an element in an array by its index.

const element = arr[5];    // Always takes the same amount of time

Visualization: No matter the size of the array, the time to access an element is constant.

O(log n): Logarithmic time - The time increases logarithmically as the input size increases. Often found in algorithms like binary search. Algorithms with O(log n) complexity reduce the problem size with each step resulting in much faster performance for large inputs.

Example: Binary search in a sorted array.

function binarySearch(arr, target) {
    let left = 0, right = arr.length - 1;
    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] === target)
            return mid;
        if (arr[mid] < target) 
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;    // Element not found
}

Visualization: The time increases slowly, even as the input size grows large.

O(n): Linear time - The time increases linearly with the input size. For example, a simple loop that goes through all elements of an array. If you double the input, the time doubles as well.

Example: Searching for an element in an unsorted array.

function findElement(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) {
            return i;
        }
    }
    return -1;    // Element not found
}

Visualization: The time increases directly in proportion to the size of the input.

O(n log n): Linearithmic time - A combination of linear and logarithmic growth, common in efficient sorting algorithms like mergesort and quicksort, where the problem size is repeatedly divided and each division is processed linearly.

Example: Merge sort.

function mergeSort(arr) {
    if (arr.length <= 1) return arr;

    const mid = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, mid));
    const right = mergeSort(arr.slice(mid));

    return merge(left, right);
}

function merge(left, right) {
    let result = [], i = 0, j = 0;
    while (i < left.length && j < right.length) {
        if (left[i] < right[j]) 
            result.push(left[i++]);
        else 
            result.push(right[j++]);
    }
    return result.concat(left.slice(i)).concat(right.slice(j));
}

Visualization: The time complexity grows faster than linear but slower than quadratic.

O(n²): Quadratic time - The time increases quadratically with the input sie. Common in algorithms with nested loops, like bubble sort.

Example: Bubble sort.

function bubbleSort(arr) {
    const n = arr.length;
    for (let i = 0; i < n - 1; i++) {
        for (let j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                const temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
    return arr;
}

Visualization: The time required grows significantly as the input size increases.

O(2ⁿ): Exponential time - The time doubles with each additional element in the input size, common in algorithms that explore all possible combinations.

Example: Calculating Fibonacci numbers using a naive recursive approach.

function fibonacci(n) {
    if (n <= 1)
        return n;

    return fibonacci(n - 1) + fibonacci(n - 2);
}

Visualization: The time complexity grows exponentially, making the algorithm infeasible for large inputs.

O(n!): Factorial time - The time grows factorially with the input size, found in algorithms that generate all permutations of a set.

Example: Generating all permutations of an array.

function permute(arr) {
    const result = [];
    if (arr.length === 0) 
        return [[]];
    const firstElem = arr[0];
    const rest = permute(arr.slice(1));
    rest.forEach((perm) => {
        for (let i = 0; i <= perm.length; i++) {
            const newPerm = perm.slice(0, i).concat([firstElem], perm.slice(i));
            result.push(newPerm);
        }
    });
    return result;
}

Visualization: The time required grows factorially, leading to extremely fast growth even with small input sizes.

O(n³): Cubic time - The complexity arises when there are three nested loops, resulting in a cubic growth of time with the input size.

Example: 3D matrix multiplication.

function cubicAlgorithm(n) {
    let count = 0;
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            for (let k = 0; k < n; k++) {
                count++;
            }
        }
    }
    return count;
}

Visualization: The time required grows cubically with the input size.

Visualizing the Differences

To help you visualize these complexities, here's a comparative graph:

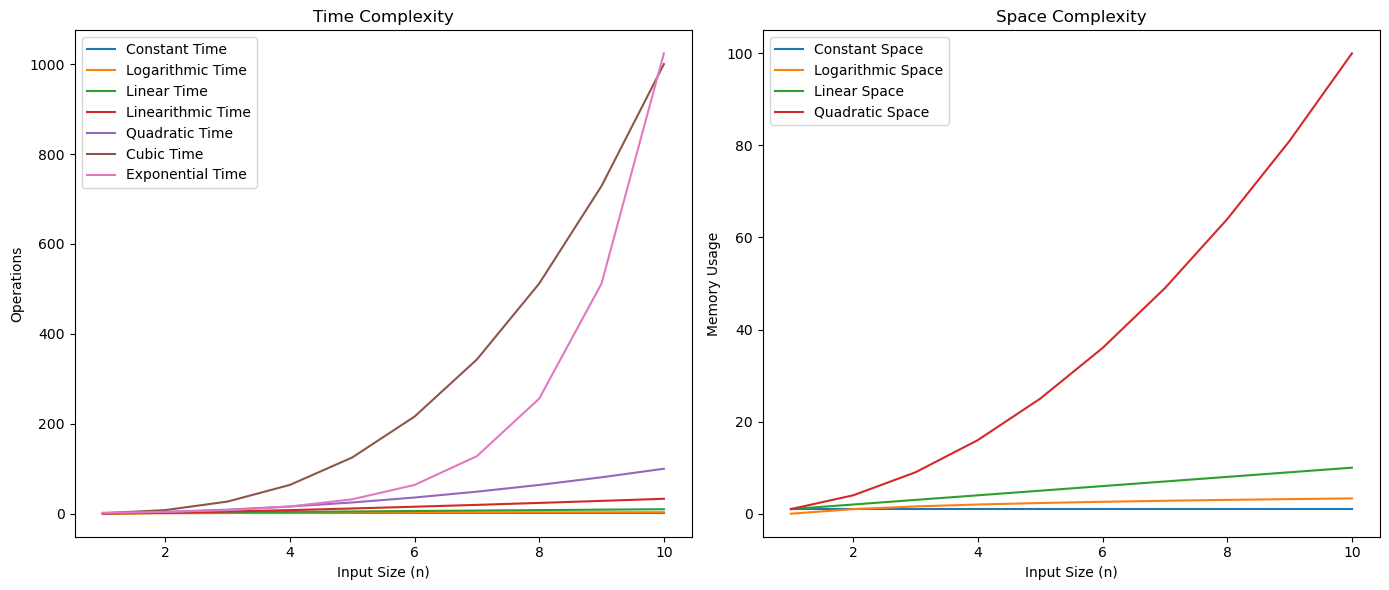
In the graph, you can see how the different time complexities (O(1) - Constant), (O(n) - Linear), (O(log n) - Logarithmic), (O(n log n) - Linearithmic), (O(n²) - Quadratic), O(n³) - Cubic), (O(2ⁿ) - Exponential) grow as the input size increases. While O(1) remains constant and O(log n) grows slowly, the higher-order complexities like O(n²) and O(2ⁿ) shoot up dramatically.

Conclusion

Understanding these different types of time complexities is essential for growing efficient code. Recognizing how your algorithms scale with input size allows you to make informed decisions, optimize performance, and ensure that your software can handle larger datasets effectively.

Keep these concepts in mind as you continue developing, and your code will be well-equipped to handle the challenges of scale. Stay tuned for next week's part of this newsletter where I will share and explain how to answer some of these complexity-related questions. So that we can learn and understand Big-O Notation, Time complexity, and Space complexity a whole lot better.

To learn more about Big-O notation, here is a neat-looking article on freeCodeCamp.

Understanding Big-O Notation