Chapter 32: Heaps(Alpha Plus Batch (Apna College)
 Rohit Gawande
Rohit GawandeTable of contents
- Introduction to Priority Queues and Heaps
- Introduction to Priority Queues (PQ)
- Priority Queues in Java Collection Framework (JCF)
- Priority Queues for Objects
- 🔍 Introduction: Why Custom Objects Need Comparison
- 🧠 What’s Happening Internally?
- 🔧 Defining the Logic: The Comparable Interface
- 📊 Visualization: Diagram Breakdown
- 🎓 Real-Life Use Case: Student Admission Queue
- Reversing the Order (Optional Insight)
- The PriorityQueue Working Mechanism in this Case
- Summary of Important Points
- 🏁 Conclusion
- 📘 Introduction to Heaps
- 🔍 What is a Heap?
- 1️⃣ Binary Tree Property
- 2️⃣ Complete Binary Tree Property
- 3️⃣ Heap Order Property (Heap Invariant)
- 🧠 Why is this Important?
- 📌 Wrap-up
- Heap Implementation Using Complete Binary Tree (CBT)
- Insertion in a Heap
- Peek from a Heap
- Remove from a Heap
- Heap Sort
- Nearby Cars Problem
- Problem Description
- Steps to Solve the Problem
- Summary
- Detailed Explanation of the Nearby Cars Problem with Code
- Connect N Ropes with Minimum Cost
- Weakest Soldier Problem
- Sliding Window Problem
- Conclusion
Introduction to Priority Queues and Heaps
Introduction to Priority Queues (PQ)
A Priority Queue (PQ) is a specialized type of queue where each element is assigned a priority. Elements with higher priority are processed before those with lower priority. Unlike a standard queue, which follows the First-In-First-Out (FIFO) principle, a priority queue ensures that elements are dequeued in the order of their priority rather than their arrival time.
For instance, if you think of a hospital emergency room, patients with more critical conditions are treated before those with less severe conditions, regardless of when they arrived. Similarly, in a priority queue, elements are removed based on their priority level.
Priority Queues in Java Collection Framework (JCF)
In Java, the PriorityQueue class is a part of the Java Collection Framework (JCF) and provides a concrete implementation of a priority queue. Internally, it uses a data structure called a binary heap to manage the elements. The elements in a PriorityQueue can be ordered either according to their natural ordering (for example, numbers in ascending order) or according to a custom order specified by a comparator.
Key Characteristics of PriorityQueue:
Natural Ordering: Elements are ordered based on their inherent properties. For example, in a queue of numbers, smaller numbers might have higher priority if we're using a min-heap approach.
Custom Ordering: You can provide a custom comparator to determine how elements are prioritized. This allows for more complex sorting criteria beyond natural ordering.
No Duplicate Elements: If an element is added to the queue multiple times, it will be stored as distinct entries if the priority remains the same.
import java.util.PriorityQueue; public class PrioQue { static class Student { int rollno; } public static void main(String[] args) { PriorityQueue<Integer>pq=new PriorityQueue<>(); pq.add(3); pq.add(4); pq.add(1); pq.add(7); while (!pq.isEmpty()) { System.out.println(pq.peek()); pq.remove(); } } }
Priority Queues for Objects
"Understanding Priority Queues with Custom Objects in Java – Student Admission Use Case"
🔍 Introduction: Why Custom Objects Need Comparison
In real-world applications like college admissions, we often need to manage data for multiple entities (like students) and prioritize them based on specific attributes (like rank). To handle such scenarios, Priority Queues (PQs) are an ideal data structure.
But here's the challenge:
Priority Queues can handle primitive types like integers directly (e.g., a queue of numbers), but when dealing with custom objects like Student, the priority queue has no idea how to compare them unless we explicitly tell it how.
This is where Java’s Comparable interface comes into play.
🧠 What’s Happening Internally?
A PriorityQueue in Java arranges its elements according to natural ordering or a custom comparator. It keeps the lowest-priority element at the front by default (min-heap behavior).
If we want to store student objects and prioritize them by rank (say, lower rank = higher priority), we need to define how two students should be compared. The queue will repeatedly compare elements as it rearranges them to maintain the priority order.
🔧 Defining the Logic: The Comparable Interface
To make our custom class (e.g., Student) work with a priority queue, we implement the Comparable interface, which means we must override the compareTo() method.
This method returns:
A negative number if the current object is less than the other.
A positive number if the current object is greater than the other.
Zero if both are equal.
In our case, the logic for comparison is simple:
this.rank - other.rank
This line tells the queue:
"Compare two students by subtracting their ranks. Whoever has the smaller rank comes first in the queue."
📊 Visualization: Diagram Breakdown

We have two student objects:
S1: "abc", Rank = 15
S2: "xyz", Rank = 15
Now, depending on what ranks are being compared:
12 - 15 = -3 → Result is negative
→ Means: Object 1 < Object 2 (S1 < S2)15 - 12 = +3 → Result is positive
→ Means: Object 1 > Object 2 (S1 > S2)15 - 15 = 0 → Result is zero
→ Means: Both objects are equal
This is the heart of how the compareTo() function governs the positioning of objects in the priority queue.
import java.util.PriorityQueue;
public class PriQJCF {
static class Student implements Comparable<Student> {
int rank;
String name;
Student(String name,int rank){
this.rank=rank;
this.name=name;
}
@Override
public int compareTo(Student s2){
return this.rank-s2.rank;
}
}
public static void main(String[] args) {
PriorityQueue<Student>pq=new PriorityQueue<>();
/* for reverse
* PriorityQueue<Student>pq=new PriorityQueue<>(Comparator.reverseOrder());
*/
pq.add(new Student("A",4));
pq.add(new Student("B",3));
pq.add(new Student("C",5));
pq.add(new Student("D",1));
while (!pq.isEmpty()) {
System.out.println(pq.peek().name+"->"+pq.peek().rank);
pq.remove();
}
}
}

🎓 Real-Life Use Case: Student Admission Queue
Suppose you're designing a Student Admission System. Each student has:
A name
A rank (lower rank means higher priority)
You’re asked to create a system that automatically arranges students based on their rank for processing admissions. That’s where the Priority Queue helps.
You:
Create a class
Studentwithnameandrankfields.Implement
Comparable<Student>and overridecompareTo().Use a
PriorityQueue<Student>which automatically keeps the lowest-rank student at the top.
So, when you insert multiple students, the queue automatically organizes them based on rank — without writing sorting logic manually.
When you poll from the queue:
First student is the one with rank 1
Next is rank 2
And so on…
Reversing the Order (Optional Insight)
If you want the reverse behavior — i.e., higher rank = higher priority (like in some competitions where higher scores matter more) — you can use a Comparator with reverse ordering. That’s an alternate approach where you don’t change the class itself but provide a comparator while creating the priority queue.
The PriorityQueue Working Mechanism in this Case
Here’s what happens step-by-step internally:
You insert 5 students: A(4), B(3), C(5), D(1), E(2)
Each time a student is added:
The priority queue uses
compareTo()to determine where the student fits.Internally it performs heapification to restore the min-heap structure.
When you start removing (polling):
The student with the lowest rank (i.e., highest priority) is removed first.
The queue restructures itself again after each removal.
Summary of Important Points
| Concept | Meaning |
| Comparable Interface | Tells Java how to compare two objects of the same class |
| compareTo() | Defines natural ordering (negative = less, positive = greater) |
| this.rank - s2.rank | Compares students by rank |
| PriorityQueue | Automatically organizes elements by priority |
| Min-Heap (Default PQ) | Element with the lowest value comes out first |
| Custom Objects in PQ | Must implement Comparable or provide Comparator |
| Equal comparison | If compareTo() returns 0, elements are considered equal |
🏁 Conclusion
When working with real-world problems like student admissions, using a Priority Queue with custom objects provides an elegant and efficient solution to maintain and retrieve elements based on priority.
Java makes this possible by offering:
The
Comparableinterface for natural ordering.The
PriorityQueueclass for automatic heap-based arrangement.
By overriding compareTo() based on attributes like rank, we can fine-tune the behavior of our queue to match the business logic. It frees developers from writing manual sorting logic and ensures that data retrieval is always in the correct priority order.
Thus, PriorityQueue combined with the Comparable interface becomes a powerful tool in Java — especially when dealing with systems that require dynamic ordering of custom objects like students, tasks, jobs, or even ride-hailing services finding the nearest car.
📘 Introduction to Heaps
Now that we’ve understood the idea of a Priority Queue, let’s take a deep dive into the data structure that powers it behind the scenes — the Heap.
You might be wondering — why are we suddenly shifting toward trees when we've been working with queues so far? Well, the answer lies in how Priority Queues are implemented. Behind the user-friendly interface of a PriorityQueue, there’s a very efficient and elegant structure working silently: a Heap. Specifically, a Binary Heap.
🔍 What is a Heap?
A Heap is a special kind of Binary Tree. But not just any binary tree — it follows some very strict rules to maintain its properties and ensure efficient performance when used inside structures like a priority queue.
When we talk about a heap, we’re really referring to an implementation of a priority queue using a binary tree that maintains a specific ordering property. And interestingly, we do not actually implement the heap using tree nodes and pointers in memory. Instead, we represent it as an array. The binary tree is just a mental model to help us visualize it.
In Java, heaps are commonly implemented using arrays, and the PriorityQueue class internally uses a binary heap to manage priority efficiently. There are two main types of heaps:
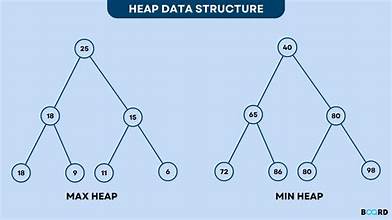
Max Heap: The largest element is always at the root. It is used when you want the maximum element to have the highest priority.
Min Heap: The smallest element is always at the root. It is used when the minimum element has the highest priority.
Now let’s understand the three major properties that define a Heap:
1️⃣ Binary Tree Property
A Heap is always a Binary Tree, which means every node can have at most two children — a left child and a right child.
This restricts the shape of the tree and keeps operations predictable. However, not every binary tree can be called a heap — it must also satisfy other conditions.
2️⃣ Complete Binary Tree Property
This is a key characteristic of heaps. A Complete Binary Tree is a binary tree in which every level is completely filled, except possibly the last level, and the last level must be filled from left to right.
This structure ensures that the binary tree remains balanced, and more importantly, it allows us to implement the tree in a linear array — no need for pointer-based node creation.
This is why heaps are so efficient. We can calculate the parent and children of any element directly using array indices:
Left child:
2*i + 1Right child:
2*i + 2Parent:
(i - 1)/2
The complete binary tree property guarantees that we always know where the next element should be inserted or removed, and that’s critical to performance.
3️⃣ Heap Order Property (Heap Invariant)
This is what truly makes a tree a heap.
Depending on whether it’s a min-heap or a max-heap, the ordering rules change:
Min Heap: Every parent node has a value less than or equal to its children. This ensures that the smallest element is always at the root.
Max Heap: Every parent node has a value greater than or equal to its children. This ensures that the largest element is always at the root.
So, the heap property governs how values are ordered across the tree — not necessarily how they are ordered linearly. In a heap, the only guaranteed ordering is between parents and their immediate children, not across entire levels.
🧠 Why is this Important?
When you insert or remove an element from a heap, you must maintain all three properties:
The binary structure (at most two children)
The complete binary shape
The heap order
That’s why after insertion or deletion, we often perform heapify operations (either upwards or downwards) to restore the heap order.
These properties make heap operations such as insert, delete, and peek extremely efficient — all typically happening in O(log n) time.
📌 Wrap-up
To summarize:
A Heap is a complete binary tree that follows a specific ordering rule (min or max).
It’s implemented using arrays, even though we visualize it as a tree.
It forms the backbone of many efficient algorithms and data structures, most notably the Priority Queue.
In Java, the PriorityQueue class is implemented using a min-heap by default.
Heap Implementation Using Complete Binary Tree (CBT)
Heaps are often implemented using a complete binary tree (CBT), which is a binary tree where all levels are fully filled except possibly for the last level, which is filled from left to right. This structure allows heaps to be efficiently represented in an array.
In an array representation:
The root of the heap is at index
0.The left child of any element at index
iis located at index2*i + 1.The right child of any element at index
iis located at index2*i + 2.The parent of any element at index
iis located at index(i - 1) / 2.
Insertion in a Heap
To insert an element into a heap:
Add the Element: Place the new element at the end of the heap (i.e., the last position in the array).
Restore Heap Property: Compare the added element with its parent and swap them if necessary to maintain the heap property. This process is called "heapify up" or "bubble up".
Repeat: Continue this process until the heap property is restored, or the element reaches the root.
Peek from a Heap
To peek at the heap, simply look at the root of the heap. In a max-heap, this will be the largest element, and in a min-heap, it will be the smallest element. Peeking does not remove the element from the heap.
import java.util.ArrayList;
public class Insert {
static class Heap {
ArrayList<Integer> p=new ArrayList<>();
public void inser(int data){
//Add at Last
p.add(data);
int child=p.size()-1;
int parent=(child-1)/2;
//Swap
while (p.get(child)<p.get(parent)) {
int temp=p.get(parent);
p.set(child, p.get(parent));
p.set(parent, temp);
}
}
public int peek(){
return p.get(0);
}
}
public static void main(String[] args) {
Heap heap=new Heap();
heap.inser(2);
}
}
Remove from a Heap
To remove the root element from a heap:
Replace the Root: Replace the root with the last element in the heap (i.e., the last position in the array).
Remove the Last Element: Remove the last element from the heap.
Restore Heap Property: Reorganize the heap to maintain its properties by "heapifying down" or "sifting down" the new root. This involves comparing the root with its children and swapping it with the appropriate child until the heap property is restored.
import java.util.ArrayList; public class Remove { static class Heap { ArrayList<Integer> p=new ArrayList<>(); public void insert(int data){ //Add at Last p.add(data); int child=p.size()-1; int parent=(child-1)/2; //Swap while (p.get(child)<p.get(parent)) { int temp=p.get(child); p.set(child, p.get(parent)); p.set(parent, temp); child=parent; parent=(child-1)/2; } } public int peek(){ return p.get(0); } private void heapify(int i){ int left=2*i+1; int right=2*i+2; int minidx=i; if(left<p.size() && p.get(minidx)>p.get(left)){ minidx=left; } if(right<p.size() && p.get(minidx)>p.get(right)){ minidx=right; } if (minidx!=i) { // Swap int temp=p.get(i); p.set(i, p.get(minidx)); p.set(minidx, temp); heapify(minidx); } } public int remove(){ int data=p.get(0); //Step 1: Swap First and Last int temp=p.get(0); p.set(0,p.get( p.size()-1)); p.set(p.size()-1, temp); //Step 2:remove p.remove(p.size()-1); //Step3: Heapify heapify(0); return data; } public boolean isEmpty(){ return p.size()==0; } } public static void main(String[] args) { Heap h=new Heap(); h.insert(3); h.insert(4); h.insert(1); h.insert(5); while(!h.isEmpty()){ System.out.println(h.peek()); h.remove(); } } }
Heap Sort
Heap sort is a sorting algorithm that uses a heap data structure to sort elements. The process involves:
Build a Max-Heap: Convert the array of elements into a max-heap.
Extract Maximum: Remove the root (maximum element) of the heap and place it at the end of the array.
Re-heapify: Restore the heap property by heapifying the root.
Repeat: Continue extracting the maximum element and re-heapifying until the heap is empty.
import java.util.Scanner; public class HeapSort { public static void heapify(int arr[],int i,int size){ int left=2*i+1; int right=2*i+2; int maxidx=i; if (left<size && arr[left]>arr[maxidx]) { maxidx=left; } if (right<size && arr[right]>arr[maxidx]) { maxidx=right; } if (maxidx!=i) { //Swap int temp=arr[i]; arr[i]=arr[maxidx]; arr[maxidx]=temp; heapify(arr, maxidx, size); } } public static void heapSort(int arr[]){ //Step 1: Bulid MaxHeap int n=arr.length; for (int i = n/2; i >=0; i--) { heapify(arr, i, n); } //Step 2: Push larget at end for (int i =n-1; i >0; i--) { //Swap int temp=arr[0]; arr[0]=arr[i]; arr[i]=temp; heapify(arr, 0, i); } } public static void main(String args[]){ int arr[]={1,2,4,5,3}; heapSort(arr); for (int i = 0; i < arr.length; i++) { System.out.print(arr[i]+" "); } } }
Nearby Cars Problem
Problem Description
Imagine you're standing at the origin of a 2D plane, which is the point (0,0). You're given the locations of N cars on this plane, and you need to find the k nearest cars to the origin. Each car's location is represented by coordinates (x, y) on this plane.
For instance, let's say you have the following cars:
Car C0 is located at (3,3)
Car C1 is located at (5,-1)
Car C2 is located at (-2,4)
In this case, you want to find the 2 nearest cars to the origin (0,0).
Steps to Solve the Problem
Calculate Distances: The distance of each car from the origin can be computed using the Euclidean distance formula. For a car located at (x, y), the distance from the origin (0,0) is given by:
{Distance} = sqrt{x^2 + y^2}
You don’t need to compute the square root for comparison purposes; the squared distance (x^2 + y^2) is sufficient.
Compute Distances for Each Car:
For Car C0 at (3,3): [ {Distance}^2 = 3^2 + 3^2 = 9 + 9 = 18 ]
For Car C1 at (5,-1): [ {Distance}^2 = 5^2 + (-1)^2 = 25 + 1 = 26 ]
For Car C2 at (-2,4): [ {Distance}^2 = (-2)^2 + 4^2 = 4 + 16 = 20 ]
Compare Distances: Next, compare these distances to determine which cars are the closest to the origin. Based on the squared distances calculated:
Car C0 has a distance squared of 18.
Car C2 has a distance squared of 20.
Car C1 has a distance squared of 26.
Clearly, Car C0 is the closest, followed by Car C2, and then Car C1.
Select the Nearest Cars: Since we need the
knearest cars, andk=2in this example, we select the two cars with the smallest distances:Car C0 (Distance squared: 18)
Car C2 (Distance squared: 20)
Print the Results: The nearest cars to the origin, based on the calculated distances, are Car C0 and Car C2.
Summary
To solve the Nearby Cars problem:
Calculate the squared distance of each car from the origin.
Compare these distances to identify the nearest cars.
Select the
kcars with the smallest distances.
import java.util.PriorityQueue;
public class NearbyCars {
static class Point implements Comparable<Point> {
int x;
int y;
int distSq;
int idx;
public Point(int x,int y,int distSq,int idx){
this.x=x;
this.y=y;
this.idx=idx;
this.distSq=distSq;
}
@Override
public int compareTo(Point p2){
return this.distSq-p2.distSq;
}
}
public static void main(String[] args) {
int pts[][]={{3,3},{5,-1},{-2,4}};
int k=2;
PriorityQueue<Point> pq=new PriorityQueue<>();
for (int i = 0; i < pts.length; i++) {
int distSq=pts[i][0]*pts[i][0]+pts[i][1]*pts[i][1];
pq.add(new Point(pts[i][0], pts[i][1], distSq,i));
}
// Nearest K cars
for (int i = 0; i < k; i++) {
System.out.println("C"+pq.remove().idx);
}
}
}
Detailed Explanation of the Nearby Cars Problem with Code
The code provided demonstrates how to solve the Nearby Cars problem using a priority queue to efficiently identify the nearest k cars from a set of given car positions. Let's break down the code and explain each part in detail:
Code Breakdown
Imports and Class Definition:
import java.util.PriorityQueue;This import statement brings in the
PriorityQueueclass from the Java Collections Framework, which is used to manage a collection of elements ordered by their priority.public class NearbyCars {The
NearbyCarsclass contains the logic to find the nearest cars.Inner Class Definition:
static class Point implements Comparable<Point> { int x; int y; int distSq; int idx; public Point(int x, int y, int distSq, int idx) { this.x = x; this.y = y; this.distSq = distSq; this.idx = idx; } @Override public int compareTo(Point p2) { return this.distSq - p2.distSq; } }The
Pointclass represents a car's position and its distance from the origin. It implements theComparableinterface to allow comparison based on the distance squared (distSq), which is used for sorting in the priority queue.Attributes:
xandyrepresent the coordinates of the car.distSqis the squared distance from the origin, calculated to avoid the overhead of computing square roots.idxis the index of the car, used to identify the car in the output.
Constructor: Initializes the car's position, distance squared, and index.
compareToMethod: This method is used to define the order in which points are stored in the priority queue. It orders the points by their distance squared (distSq), ensuring that the closest points come first.
Main Method:
public static void main(String[] args) { int pts[][] = {{3, 3}, {5, -1}, {-2, 4}}; int k = 2; PriorityQueue<Point> pq = new PriorityQueue<>();pts[][]is a 2D array where each inner array represents the coordinates of a car.kis the number of nearest cars you want to find.pqis a priority queue that will storePointobjects and automatically order them based on their distance squared.
for (int i = 0; i < pts.length; i++) {
int distSq = pts[i][0] * pts[i][0] + pts[i][1] * pts[i][1];
pq.add(new Point(pts[i][0], pts[i][1], distSq, i));
}
This loop iterates through each car's position, calculates the squared distance from the origin (to avoid computing the square root), and adds a new Point object to the priority queue.
for (int i = 0; i < k; i++) {
System.out.println("C" + pq.remove().idx);
}
}
This loop extracts the k nearest cars from the priority queue. Since the priority queue is ordered by distance, removing elements from it gives the nearest cars first. The idx attribute is used to identify and print each car.
How It Works
Distance Calculation:
- The squared distance is calculated for each car using the formula ( {distSq} = x^2 + y^2 ). This avoids the computational expense of taking the square root, which is unnecessary for comparison purposes.
Priority Queue Operations:
- The priority queue automatically maintains the order of elements based on the distance squared. The closest cars (with the smallest distance squared) are always at the front of the queue.
Extracting Nearest Cars:
- By removing the top
kelements from the priority queue, you get the indices of theknearest cars. These indices correspond to the closest cars based on their distance from the origin.
- By removing the top
Summary
This code efficiently finds and prints the nearest k cars from a given list of positions. By using a priority queue, it maintains the nearest cars in a sorted order based on their distance from the origin. The approach ensures that the solution is both effective and efficient, leveraging the properties of the priority queue to handle the sorting and extraction of nearest elements.
Connect N Ropes with Minimum Cost
In this problem, you need to connect N ropes of varying lengths into a single rope with the minimum cost. The cost to connect two ropes is the sum of their lengths. To minimize the total cost, you can use a priority queue to always connect the two shortest ropes first.
Weakest Soldier Problem
The weakest soldier problem involves finding the soldier with the least strength in a line of soldiers. By using a priority queue, you can efficiently determine which soldier has the lowest strength by maintaining an ordered list based on strength values.
Sliding Window Problem
The sliding window problem involves finding optimal solutions within a moving window of elements. This approach is useful for problems like finding the maximum or minimum value in a subarray. A priority queue or deque can be used to manage and update the window's content efficiently as it slides over the sequence.
Conclusion
Understanding priority queues and heaps is fundamental to solving a wide range of computational problems efficiently. Priority queues are versatile data structures that manage elements based on their priority rather than their order of insertion, making them invaluable for tasks such as scheduling, resource management, and real-time systems. The underlying heap structure enables priority queues to offer optimal performance in insertion and removal operations.
Heaps, with their complete binary tree representation, provide a powerful mechanism for implementing priority queues. The heap property ensures that the highest or lowest priority element is always accessible, which is essential for efficiently managing dynamic sets of elements. By maintaining this property, heaps facilitate operations like insertion, deletion, and sorting with predictable performance.
Practical problems such as connecting ropes with minimal cost, finding nearby cars, and sorting elements can all benefit from the principles of heaps and priority queues. Their applications extend to real-world scenarios, including task scheduling, resource allocation, and data stream management.
In summary, mastering priority queues and heaps equips you with the tools to tackle complex problems efficiently and effectively, making these concepts a crucial part of any programmer’s toolkit. Whether you’re dealing with dynamic data sets or optimizing performance for specific tasks, understanding and applying these data structures will significantly enhance your problem-solving capabilities.
Subscribe to my newsletter
Read articles from Rohit Gawande directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
Rohit Gawande
Rohit Gawande
🚀 Tech Enthusiast | Full Stack Developer | System Design Explorer 💻 Passionate About Building Scalable Solutions and Sharing Knowledge Hi, I’m Rohit Gawande! 👋I am a Full Stack Java Developer with a deep interest in System Design, Data Structures & Algorithms, and building modern web applications. My goal is to empower developers with practical knowledge, best practices, and insights from real-world experiences. What I’m Currently Doing 🔹 Writing an in-depth System Design Series to help developers master complex design concepts.🔹 Sharing insights and projects from my journey in Full Stack Java Development, DSA in Java (Alpha Plus Course), and Full Stack Web Development.🔹 Exploring advanced Java concepts and modern web technologies. What You Can Expect Here ✨ Detailed technical blogs with examples, diagrams, and real-world use cases.✨ Practical guides on Java, System Design, and Full Stack Development.✨ Community-driven discussions to learn and grow together. Let’s Connect! 🌐 GitHub – Explore my projects and contributions.💼 LinkedIn – Connect for opportunities and collaborations.🏆 LeetCode – Check out my problem-solving journey. 💡 "Learning is a journey, not a destination. Let’s grow together!" Feel free to customize or add more based on your preferences! 😊