Arithmetic Expressions Evaluator: Part 1

Previous Posts:

The Journey is Just Beginning

It’s been a long journey, but we’ve finally reached the point where we’re ready to create an arithmetic expressions evaluator. This program will demonstrate the essential steps required to build more complex projects, such as programming languages.

We’re going to focus on the Lexer and AST Node structures in this part, and in the next article, we’ll finalize our program and evaluate arithmetic expressions.

Project Structure

As we discussed earlier, creating such an evaluator requires at least three components: a Lexer, a Parser, and an Interpreter. The Interpreter will take the AST and reduce everything to a single value. With this in mind, our project structure will look as follows:

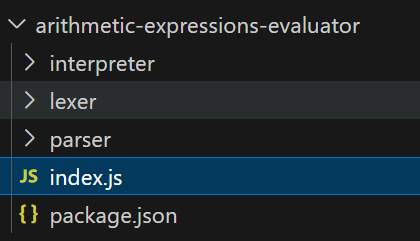
We have a simple Node.js project with separate folders for the interpreter, parser, and lexer. There's a root index.js file that we'll use as the starting point, and, of course, a package.json file.

In the package.json file, we will have a very simple configuration:

{
  "name": "arithmetic-expressions-evaluator",
  "version": "1.0.0",
  "main": "./index.js",
  "license": "MIT",
  "description": "Arithmetic Expressions Evaluator",
  "author": "Arman Takmazyan",
  "sideEffects": false,
  "scripts": {
    "start": "node ./index.js"
  }
}

This configuration sets up a basic Node.js project named "arithmetic-expressions-evaluator". It specifies the entry point as index.js and includes a start script to run the project. The configuration also provides basic metadata like version, author, and license.

Lexer

As we already know, the lexer's primary responsibility is to read text, or source code, and separate it into tokens, which are the building blocks of a language's structure. Now let us explore the process of developing such a program.

First of all, we need to define a TOKEN_KIND object, which is a collection of various token types. It includes types such as "Number", "BinaryOperator", "OpenParen", and "CloseParen", among others. Each type represents a different kind of text snippet that the program might encounter, such as numbers, mathematical operators, or parentheses. Additionally, TOKEN_KIND also includes a special type named "EOF", which stands for "End Of File". This is used to signify the end of the text being processed, serving as a crucial marker in text analysis and processing.

Let's create this constant for our Lexer and place it in the constants.js file within its folder.

const TOKEN_KIND = {
  Number: 'Number',
  BinaryOperator: 'BinaryOperator',
  OpenParen: 'OpenParen', // (
  CloseParen: 'CloseParen', // )
  Space: 'Space',
  Newline: 'Newline',
  EOF: 'EOF', // Signified the end of file
};

Next, we can create a TokenType class, which serves as a blueprint for creating objects that provide detailed descriptions of each token type. Each TokenType object is assigned a name corresponding to one of those listed in TOKEN_KIND and is associated with a regular expression pattern. These regex patterns are specifically designed to identify valid tokens within the text. For example, the regex pattern for a number is crafted to recognize sequences of digits, ensuring that only valid numeric tokens are identified. We can create this class in the token.js file.

class TokenType {
  // name: TokenKind;
  // regex: string;
  constructor({ name, regex }) {
    this.name = name;
    this.regex = regex;
  }
}

Following this, the Token class defines the actual tokens encountered in the text. Each token is an instance of this class and contains information about what type of token it is (TokenType) and its specific text value. We can write it below the TokenType class and export both.

class TokenType {
  // name: TOKEN_KIND;
  // regex: string;
  constructor({ name, regex }) {
    this.name = name;
    this.regex = regex;
  }
}

class Token {
  // type: TokenType;
  // value: string;
  constructor({ type, value }) {
    this.type = type;
    this.value = value;
  }
}

module.exports = {
  TokenType,
  Token,
};

We need a few more constants, though. Specifically, we want constants that map token types to the regular expressions needed to identify those token types, making it easier to create the Lexer class. One of these constants is TOKEN_SPECS, which is a crucial part of this setup. TOKEN_SPECS is a collection of token types, created based on TOKEN_KIND. This collection defines the kinds of tokens the program can recognize and the regular expression patterns used to identify them.

const { TokenType } = require('./token');

const TOKEN_KIND = {
  Number: 'Number',
  BinaryOperator: 'BinaryOperator',
  OpenParen: 'OpenParen', // (
  CloseParen: 'CloseParen', // )
  Space: 'Space',
  Newline: 'Newline',
  EOF: 'EOF', // Signified the end of file
};

const BINARY_OPERATOR = {
  PLUS: '+',
  MINUS: '-',
  MULTIPLY: '*',
  DIVIDE: '/',
};

const TOKEN_SPECS = {
  [TOKEN_KIND.Number]: new TokenType({
    name: TOKEN_KIND.Number,
    regex: '\\d+(\\.\\d+)?',
  }),
  [TOKEN_KIND.BinaryOperator]: new TokenType({
    name: TOKEN_KIND.BinaryOperator,
    regex: '(\\+|-|\\*|\\/)',
  }),
  [TOKEN_KIND.Newline]: new TokenType({
    name: TOKEN_KIND.Newline,
    regex: '[\\n]+',
  }),
  [TOKEN_KIND.Space]: new TokenType({
    name: TOKEN_KIND.Space,
    regex: '[ \\t\\r]',
  }),
  [TOKEN_KIND.OpenParen]: new TokenType({
    name: TOKEN_KIND.OpenParen,
    regex: '\\(',
  }),
  [TOKEN_KIND.CloseParen]: new TokenType({
    name: TOKEN_KIND.CloseParen,
    regex: '\\)',
  }),
  [TOKEN_KIND.EOF]: new TokenType({
    name: TOKEN_KIND.EOF,
    regex: '',
  }),
};

const TOKEN_PATTERNS_LIST = [...Object.values(TOKEN_SPECS)];

module.exports = {
  TOKEN_KIND,
  BINARY_OPERATOR,
  TOKEN_SPECS,
  TOKEN_PATTERNS_LIST,
};

You can also see that we created the BINARY_OPERATOR constant, which we will use later to identify different types of binary operators, as well as the TOKEN_PATTERNS_LIST constant.

The TOKEN_PATTERNS_LIST aggregates all the token specifications from TOKEN_SPECS into a single list. This list can be used by the program to check the text it's analyzing, matching each piece of text with the appropriate token type.

Now we have everything we need to create a lexer. In the index.js file in the same folder, we can start doing that.

class Lexer {
  constructor(sourceCode) {
    this.sourceCode = sourceCode;
    this.position = 0;
    this.tokenList = [];
  }
}

Of course, our lexer instance should have at least three properties: sourceCode, position, and tokenList. We will pass the source code as a parameter when instantiating the class. The sourceCode will be used to analyze the text character by character. As we go through each part of the text, we will update the position (acting as a cursor) to move to the next token and collect all the tokens in the tokenList property.

Let’s consider how the tokenize() method might be implemented. We'll focus on writing the core logic of the function, even without creating all the necessary helper functions at this stage. Let's focus on how we want to traverse the text, identifying and collecting each word:

const { Token } = require('./token');
const { TOKEN_SPECS } = require('./constants');

class Lexer {
  constructor(sourceCode) {
    this.sourceCode = sourceCode;
    this.position = 0;
    this.tokenList = [];
  }

  tokenize() {
    while (this.position < this.sourceCode.length) {
      const token = this.nextToken();
      if (this.includeToken(token)) {
        this.tokenList.push(token);
      }
    }

    // Push EOF token to signal end of source code to the parser
    this.tokenList.push(
      new Token({
        type: TOKEN_SPECS.EOF,
        value: '',
      }),
    );

    return this.tokenList;
  }
}

The tokenize() method is responsible for converting the entire source code into tokens. It works by continuously looping through the source code, generating tokens with the nextToken() method. Relevant tokens are added to the tokenList, and once all tokens are processed, an EOF (End of File) token is appended to signal the end of the source code. The method then returns the complete list of tokens, ready for parsing.

To collect only relevant tokens — since, in our case, we don’t need information about whitespace and newline characters during the parsing stage — you might have already noticed the use of the includeToken(token) method. Implementing this method will be easy:

includeToken(token) {
  if (
    !token ||
    token.type.name === TOKEN_KIND.Space ||
    token.type.name === TOKEN_KIND.Newline
  ) {
    return false;
  }

  return true;
}

Let's now concentrate on the heart and soul of our lexer—the nextToken() method:

nextToken() {
  // EOF reached
  if (this.position >= this.sourceCode.length) return null;

  for (const tokenType of TOKEN_PATTERNS_LIST) {
    const regex = new RegExp(`^${tokenType.regex}`);
    const match = regex.exec(this.sourceCode.slice(this.position));
    const [matchedString] = match ?? [];

    if (matchedString) {
      const tokenEndPosition = this.position + matchedString.length;
      const token = new Token({
        type: tokenType,
        value: matchedString,
      });

      this.position = tokenEndPosition;
      return token;
    }
  }

  const unexpectedCharacter = this.sourceCode[this.position];

  throw new Error(
    `Unexpected character ${unexpectedCharacter} at position ${this.position}`,
  );
}

The nextToken() method is designed to extract the next token from the source code. It begins by checking if we've reached the end of the input. If not, it loops through a list of token patterns, trying to find a match starting from the current position in the source code. When a match is found, it creates a token, updates the position, and returns the token. If no match is found, it throws an error for any unexpected character, indicating that something in the source code doesn't match any known token pattern. This is a lexical error, which might occur before the syntax analysis stage.

Using all the instruments that were previously defined, the Lexer class looks like this:

const { Token } = require('./token');
const { TOKEN_KIND, TOKEN_PATTERNS_LIST, TOKEN_SPECS } = require('./constants');

class Lexer {
  constructor(sourceCode) {
    this.sourceCode = sourceCode;
    this.position = 0;
    this.tokenList = [];
  }

  tokenize() {
    while (this.position < this.sourceCode.length) {
      const token = this.nextToken();
      if (this.includeToken(token)) {
        this.tokenList.push(token);
      }
    }

    // Push EOF token to signal end of source code to the parser
    this.tokenList.push(
      new Token({
        type: TOKEN_SPECS.EOF,
        value: '',
      }),
    );

    return this.tokenList;
  }

  nextToken() {
    // EOF reached
    if (this.position >= this.sourceCode.length) return null;

    for (const tokenType of TOKEN_PATTERNS_LIST) {
      const regex = new RegExp(`^${tokenType.regex}`);
      const match = regex.exec(this.sourceCode.slice(this.position));
      const [matchedString] = match ?? [];

      if (matchedString) {
        const tokenEndPosition = this.position + matchedString.length;
        const token = new Token({
          type: tokenType,
          value: matchedString,
        });

        this.position = tokenEndPosition;
        return token;
      }
    }

    const unexpectedCharacter = this.sourceCode[this.position];

    throw new Error(
      `Unexpected character ${unexpectedCharacter} at position ${this.position}`,
    );
  }

  includeToken(token) {
    if (
      !token ||
      token.type.name === TOKEN_KIND.Space ||
      token.type.name === TOKEN_KIND.Newline
    ) {
      return false;
    }

    return true;
  }
}

module.exports = {
  Lexer,
};

lexical-analysis-01

So, the Lexer is an essential component that breaks down source code into tokens, simplifying the process of analyzing and interpreting programming languages.

Eliminating Left Recursion

We need to create our parser using the arithmetic expressions grammar that we have created earlier. But let's take a look at it one more time:

<expression> ::= <term> | <expression> + <term> | <expression> - <term>

<term> ::= <factor> | <term> * <factor> | <term> / <factor>

<factor> ::= <number> | ( <expression> )

<number> ::= <digit> | <number> <digit>

<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Since we're going to implement a recursive descent parser, you might have already noticed an important problem here. A recursive descent parser is a kind of top-down parser built from a set of recursive procedures, where each procedure implements one of the non-terminals of the grammar. It processes the input from left to right, following a top-down approach by starting with the start symbol, but technically, the construction of AST nodes happens from the bottom up, building from the simplest elements to the more complex structures. Recursive descent parsers cannot parse this grammar because it contains left recursion.

A grammar rule is left-recursive if the non-terminal on the left side of a rule can directly or indirectly appear as the first symbol on the right side of the rule. For instance:

S → Sb | a

This grammar contains left recursion because the non-terminal S recurs on the left side of the production. In other words, in order to parse S, we need to parse S so that we can parse S, and so on.

We can observe the same behavior for this rule from our arithmetic expressions grammar:

<expression> ::= <term> | <expression> + <term> | <expression> - <term>

There is also a concept known as indirect left recursion, which occurs when a non-terminal leads to a left recursion through a series of rules, rather than directly. It's important to understand that while recursion is acceptable in grammars designed for recursive descent parsers, left recursion, whether direct or indirect, must be avoided.

We need to somehow transform this grammar in a way that eliminates left recursion while preserving associativity, precedence, and other properties of the arithmetic operators.

Let's see how the "expression" rule would look with right recursion:

<expression> ::= <term> | <term> + <expression> | <term> - <expression>

However, this modification also alters the left/right associativity of the operators. Additionally, we still have one more problem. Our parser needs to decide which production rule to use. If, for instance, it initially chooses to apply the rule <term> + <expression> but then realizes partway through the expression that it should have used <term> - <expression>, it must start over. This increases complexity, which we aim to avoid.

Generally, backtracking happens when derivations from a rule share initial elements, like in the case of:

X → Yz | Yx

To solve this, we use a method called left factoring. This means we take out the part that's the same in both rules and make a new rule for it. After applying left factoring, our rule will look like this:

<expression> ::= <term> <expression'>

<expression'> ::= + <term> <expression'> | - <term> <expression'> | ε

We introduced a new non-terminal called <expression'> to eliminate direct left recursion. We also use ε to let the parser know when to stop going deeper into recursion. After the transformations, the new version of the grammar is ready for a recursive descent parser without backtracking. This prevents endless loops and ensures that, at every step, the parser clearly knows which rule to use based on the next symbol it sees.

You can learn more about left recursion elimination by following this link: Left Recursion Elimination. Professor Marc Moreno Maza provides a detailed explanation on the topic.

After applying these transformations to all the operators in our arithmetic expressions grammar, we have:

<expression> ::= <term> <expression'>

<expression'> ::= + <term> <expression'> | - <term> <expression'> | ε

<term> ::= <factor> <term'>

<term'> ::= * <factor> <term'> | / <factor> <term'> | ε

<factor> ::= <number> | ( <expression> )

<number> ::= <digit> | <number> <digit>

<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

However, as we noticed earlier, these changes unintentionally altered the operators' associativity, disrupting our grammar to some extent. So, how do we fix this? The solution lies at the parser level. During parsing, we will manually correct the associativity of the operators that were accidentally changed.

Many people skip explaining this aspect when discussing recursive descent parsers. In general, we often make adjustments during parsing to handle associativity, which is a limitation we need to consider. We'll explore how this works technically in the next chapter.

Visitor Pattern

Now we have an appropriate grammar for our recursive descent parser without backtracking. However, there's one more aspect we need to discuss: the Visitor pattern.

Visitor is a behavioral design pattern that lets you separate algorithms from the objects on which they operate. This pattern is particularly beneficial in the development of parsers, interpreters, and compilers, as it enables the addition of new operations without modifying the objects on which those operations are performed.

In the visitor.js file located in our parser folder, let's add the following code:

class ASTVisitor {
  visitNumberNode(node) {
    throw new Error('visitNumberNode not implemented');
  }

  visitBinaryOperationNode(node) {
    throw new Error('visitBinaryOperationNode not implemented');
  }
}

module.exports = {
  ASTVisitor,
};

This ASTVisitor class outlines the basic structure for a visitor capable of handling different types of nodes. Each visit method is specialized to interact with a specific node type. By throwing an error, it requires that any subclass must implement these methods, ensuring that each node type can be appropriately handled.

Schematically, we can represent the visitor pattern logic this way:

So, every node must have the accept method, which lets it work with a Visitor object to perform specific actions. This approach simplifies adding new actions and manages complexity as parsers, interpreters, and compilers grow with more node types and actions.

In the astNode.js file within the same parser folder, we should include the following code:

class ASTNode {
  constructor(type) {
    this.type = type;
  }

  accept(_visitor) {
    throw new Error('accept not implemented');
  }
}

This is the base class for all nodes in the AST. It serves as a generic node with a minimal set of properties and methods necessary for all types of nodes.

The type property is a string that indicates the node's type (e.g., "Number" or "BinaryOperation"). This helps identify the kind of operation or value that the node represents.

The accept(visitor) method by default throws an error, indicating that any subclass should implement this method.

Let's now create NumberNode and BinaryOperationNode using our base ASTNode class.

For the NumberNode, we should write the following:

class NumberNode extends ASTNode {
  constructor(value) {
    super(TOKEN_KIND.Number);
    this.value = value;
  }

  accept(visitor) {
    return visitor.visitNumberNode(this);
  }
}

This is a leaf node in the tree, meaning it does not have child nodes. The value property represents a numerical value associated with this node. It overrides the accept method to invoke the visitNumberNode function on the visitor, passing this as the argument. This allows the visitor to handle the numerical value of this node.

BinaryOperationNode will function as follows:

class BinaryOperationNode extends ASTNode {
  constructor(operator, left, right) {
    super(TOKEN_KIND.BinaryOperator);
    this.operator = operator;
    this.left = left;
    this.right = right;
  }

  accept(visitor) {
    return visitor.visitBinaryOperationNode(this);
  }
}

This node represents a binary operation (e.g., addition, subtraction, multiplication, division) within the AST. It functions as a parent node in the tree, indicating that it contains child nodes.

The 'operator' property is a string that represents the operator of the binary operation (e.g., "+", "-", "*", "/"). left denotes the left child node of the binary operation, which can be another BinaryOperationNode or a NumberNode, enabling nested operations. Similarly, right represents the right child node of the binary operation, with the same potential types as left.

Similar to the NumberNode, this node also overrides the accept method to invoke visitBinaryOperationNode on the visitor, passing this as the argument. This enables the visitor to process the binary operation represented by this node, including evaluating the operation based on the operator and the values or additional operations represented by the left and right child nodes.

We aim to represent mathematical expressions as a tree structure, where each node has a distinct role and a relationship with other nodes. The NumberNode signifies values, whereas the BinaryOperationNode signifies operations involving two values or sub-expressions. The utilization of the Visitor pattern via the accept method enables external entities, such as interpreters, to "visit" each node and perform actions, such as evaluation or translation, based on the node's type and properties. This knowledge is essential for understanding how compilers and interpreters work with source code, including parsing, representing, and modifying it.

By gathering all these functions in our astNode.js file, we now have the following:

const { TokenKind } = require('../lexer/constants');

class ASTNode {
  constructor(type) {
    this.type = type;
  }

  accept(_visitor) {
    throw new Error('accept not implemented');
  }
}

class NumberNode extends ASTNode {
  constructor(value) {
    super(TokenKind.Number);
    this.value = value;
  }

  accept(visitor) {
    return visitor.visitNumberNode(this);
  }
}

class BinaryOperationNode extends ASTNode {
  constructor(operator, left, right) {
    super(TokenKind.BinaryOperator);
    this.operator = operator;
    this.left = left;
    this.right = right;
  }

  accept(visitor) {
    return visitor.visitBinaryOperationNode(this);
  }
}

module.exports = {
  NumberNode,
  BinaryOperationNode,
};

CLI Setup for Our Evaluator

We’re not going to create or evaluate an AST in this chapter, but let's test our tokenizer. To do this, go to the root directory and add the following logic to the index.js file:

const readline = require('readline');
const { Lexer } = require('./lexer');

const readlineInterface = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

function waitForUserInput() {
  readlineInterface.question('Input expression: ', function (input) {
    if (input.toLocaleLowerCase() === 'exit') {
      return readlineInterface.close();
    }

    if (!input.trim()) {
      return waitForUserInput();
    }

    const lexer = new Lexer(input);
    const tokens = lexer.tokenize();

    console.log('Output: ', tokens);
    waitForUserInput();
  });
}

waitForUserInput();

This code sets up a simple command-line interface that reads user input, tokenizes the input using a Lexer class, and then prints the resulting tokens. It repeatedly prompts for input until the user types "exit".

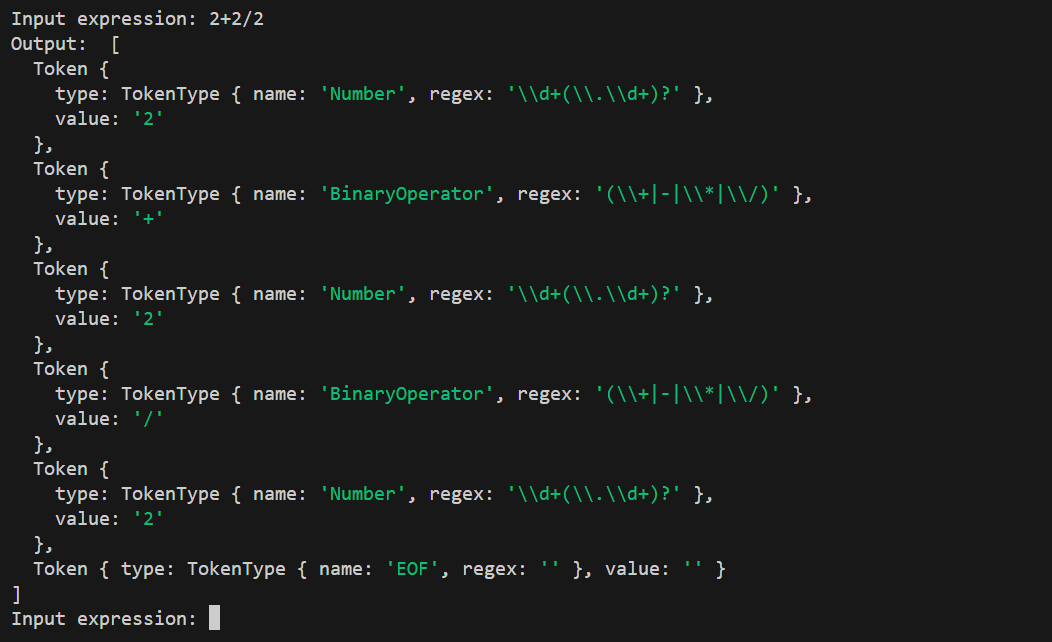
If we open a terminal in the project's root directory and run the start script from package.json, we can test it:

Conclusion

In this first part, we developed the Lexer and explored AST Node structures for our arithmetic expressions evaluator. We covered lexical analysis, resolved the left recursion problem, and introduced the Visitor pattern. With these components in place, we’re ready to build the parser and interpreter in the next article, where we’ll evaluate and compute the results of arithmetic expressions. Stay tuned!