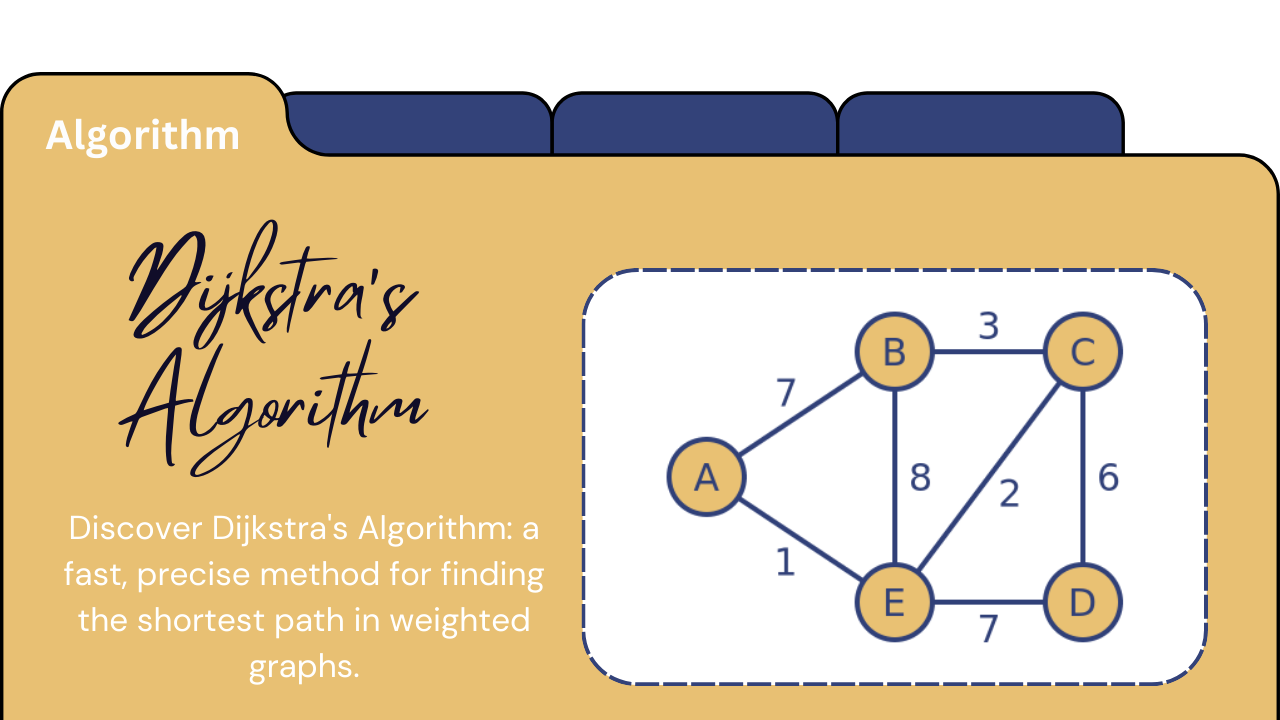
What is Dijkstra's Algorithm?

Dijkstra's Algorithm is a renowned algorithm used to find the shortest paths between nodes in a graph. It is widely used in routing and as a foundation for various network-related applications. Whether you're navigating through a map or optimizing network traffic, Dijkstra's Algorithm provides an efficient way to determine the shortest path.

---

Steps of Dijkstra's Algorithm:

1. Initialization:

   • Set the distance to the source node as 0 and to all other nodes as infinity.

   • Add all nodes to a priority queue with their initial distances to keep track of the nodes with the shortest known distance..

2. Relaxation:

   • Extract the node with the smallest distance from the priority queue.

   • For each neighboring node, calculate the potential new distance and update it if it's shorter than the current known distance.

   • Repeat until all nodes have been processed.

3. Path Reconstruction:

   • Once the shortest paths are determined, reconstruct the shortest path from the source node to the target node using the recorded distances and predecessors.

---

Let's understand the journey to the shortest path!

The algorithm iteratively selects the closest unvisited node and updates the distances of its neighbors. This process continues until the shortest path to each node is found.

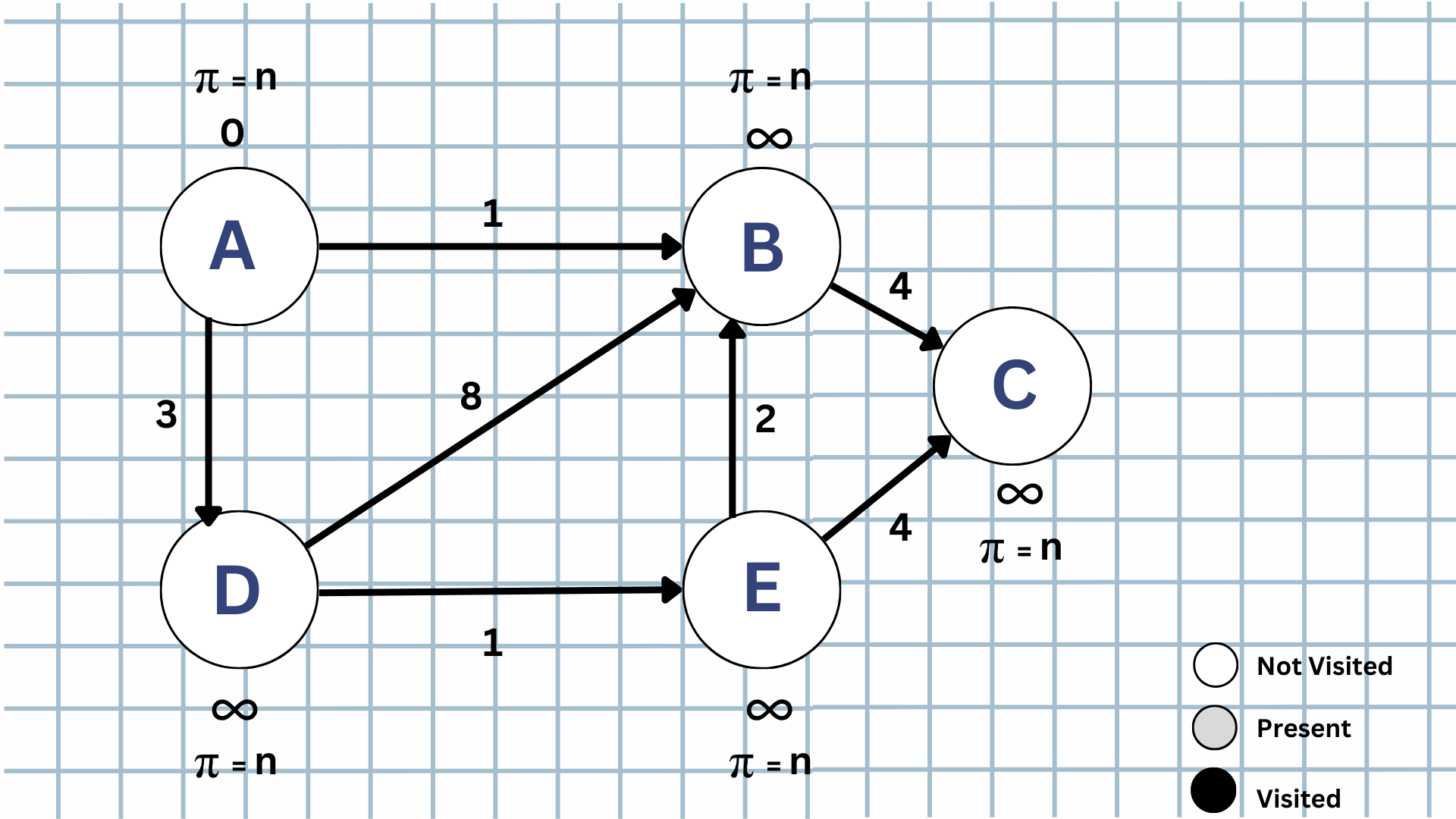
The time complexity is O((V + E) log V), where V is the number of vertices and E is the number of edges.

STEP-1:

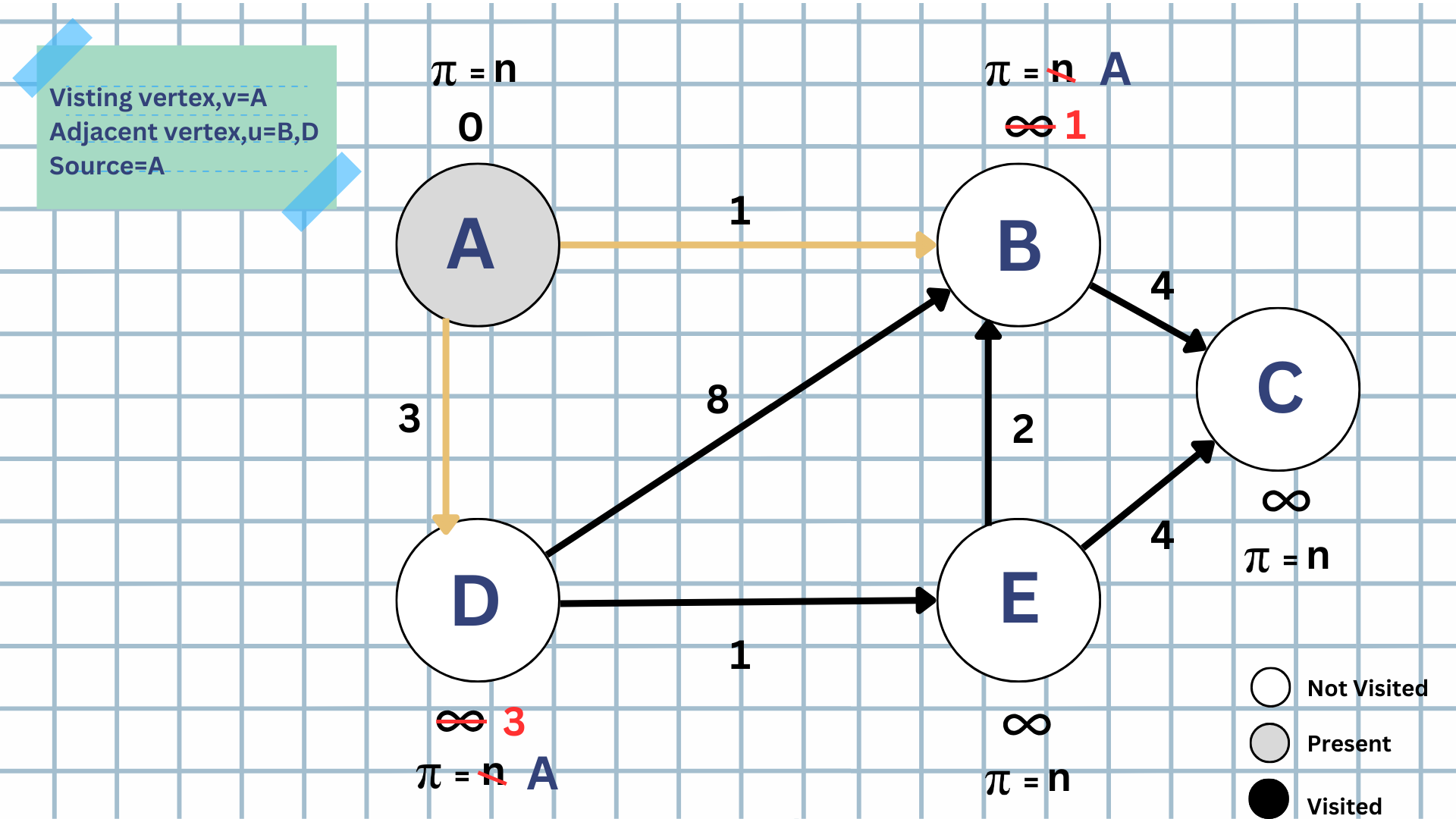
As we consider 'Vertex-A' as our source, its distance from itself is zero. Now, as we travel to the closest unvisited nodes, we see that the adjacent vertices to Vertex-A are D and B.

By relaxing both B and D, we see that the potential new distance is less than infinity. So, we update the value from infinity to the potential new distance. Also, we should remember to update the parent identifier. In both cases, the parent is A.

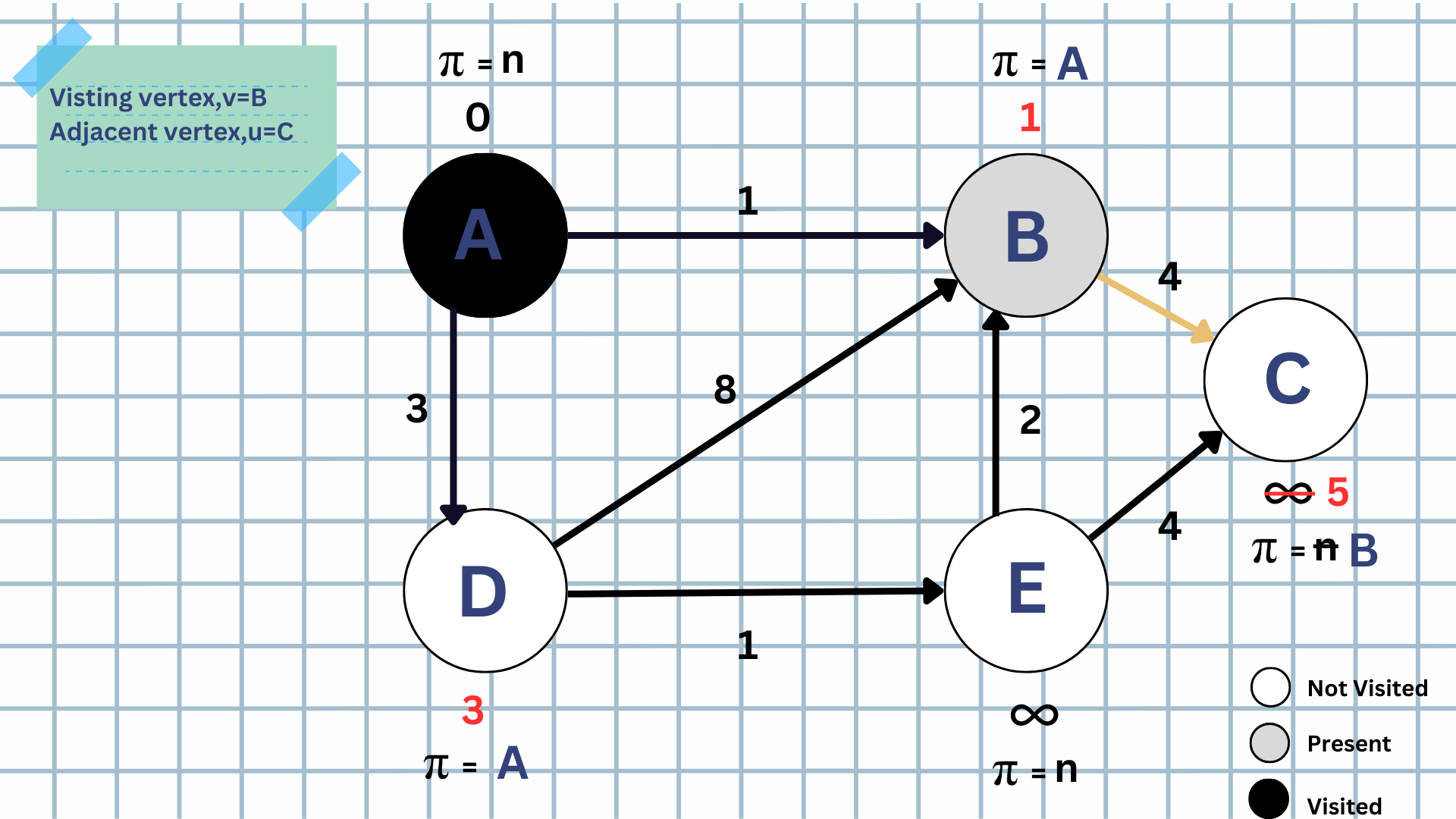
STEP-2:

Now, we choose the next vertex to visit based on its minimum weighted edge value. So, we select "Vertex-B" as our next current visiting point. We then repeat the same process as we did in Step-1.

STEP-3

While currently at "Vertex-D," we see there are two outgoing edges. For the edge from D to B, the new potential distance was supposed to be 11, which is less than the current known distance. Because of this, we don't update its value and keep it as it is. Then, we move forward.

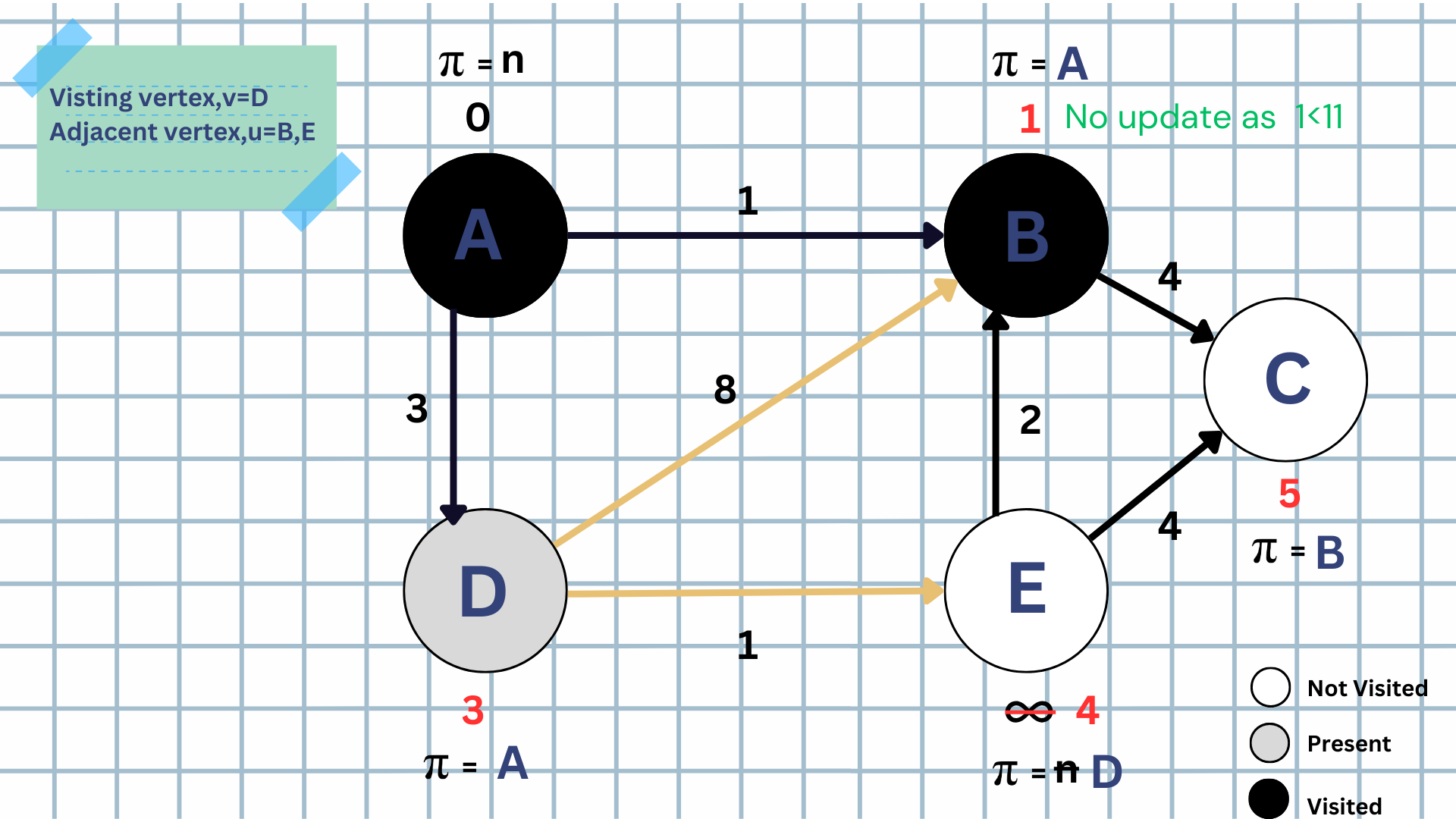
STEP-4:

We stick to our understanding of the algo and carry out our same approach for "Vertex-E".

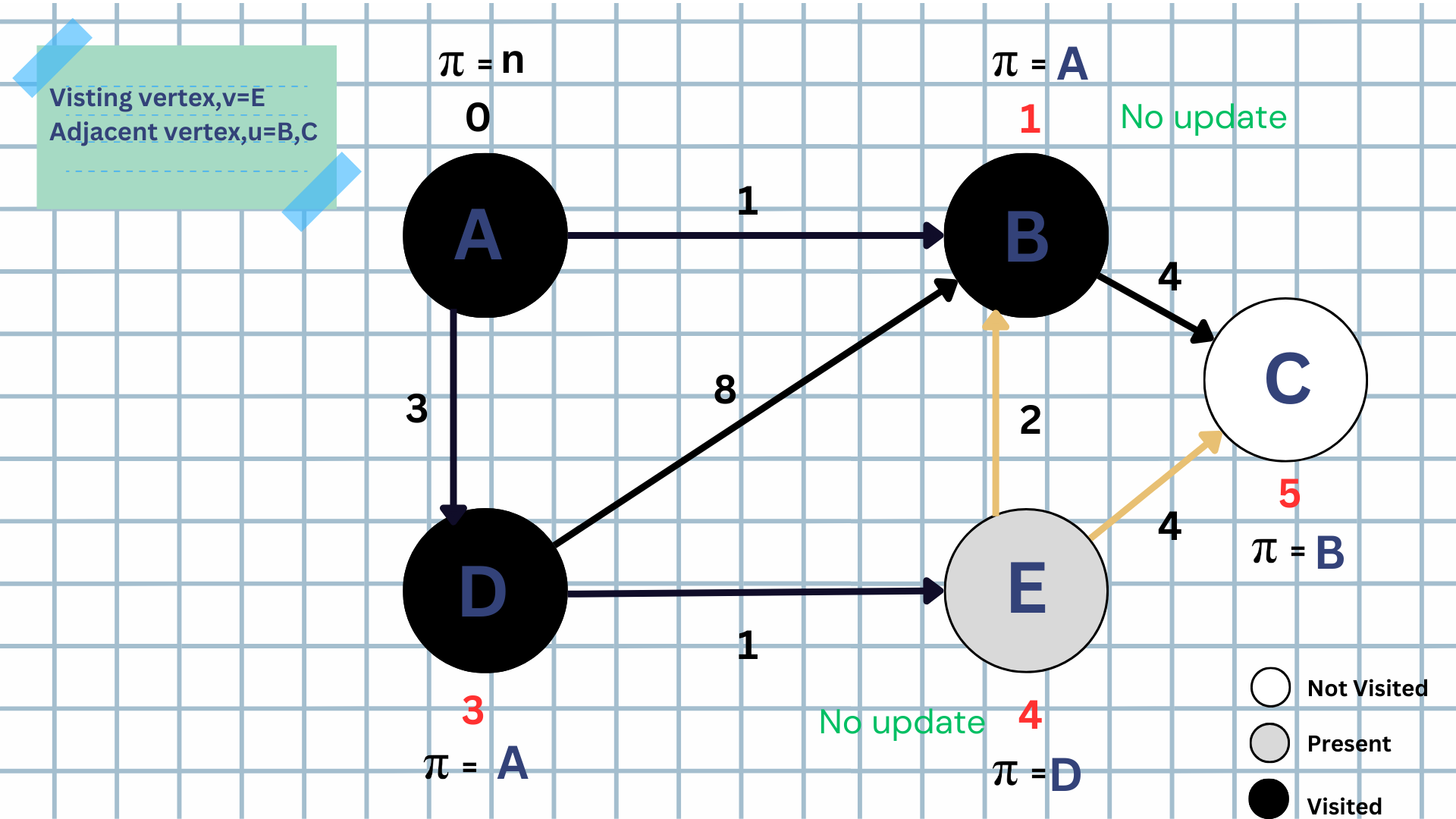
STEP-5:

Now, we reach our last vertex and see no adjacent vertices. So, we mark that node as visited.

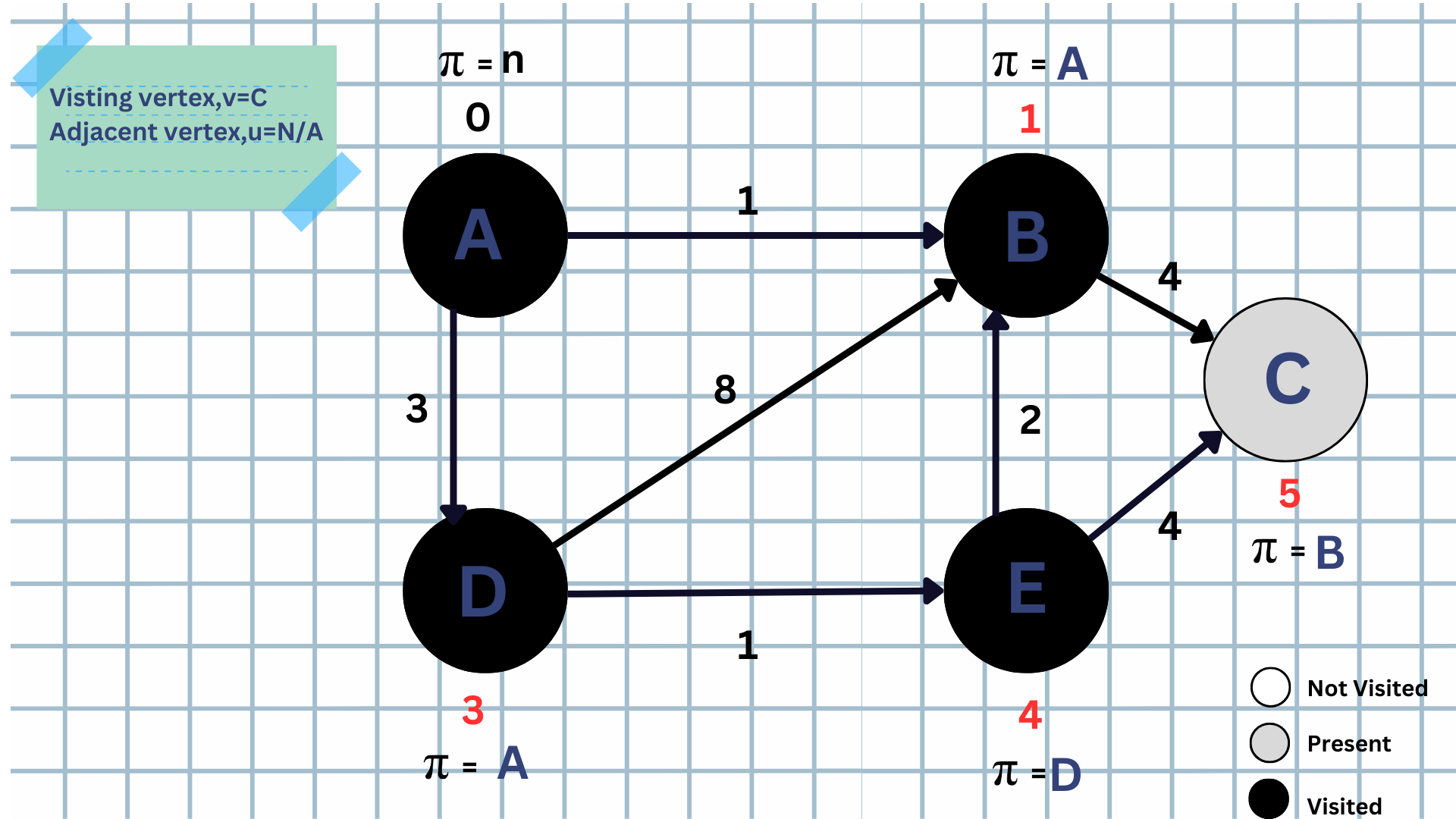
STEP-6:

Yahoo! Our stimulation is done as all the vertices are visited !

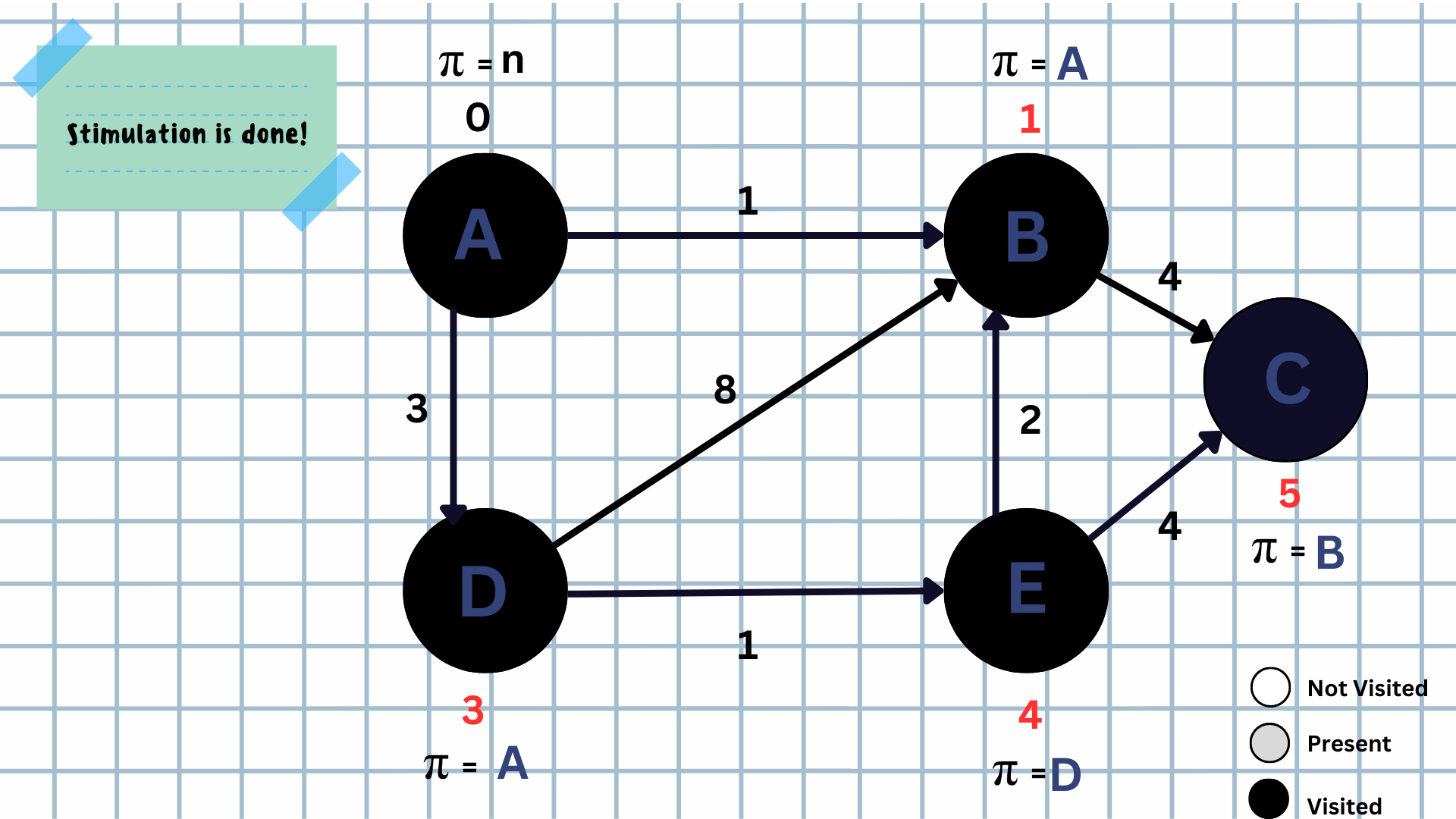
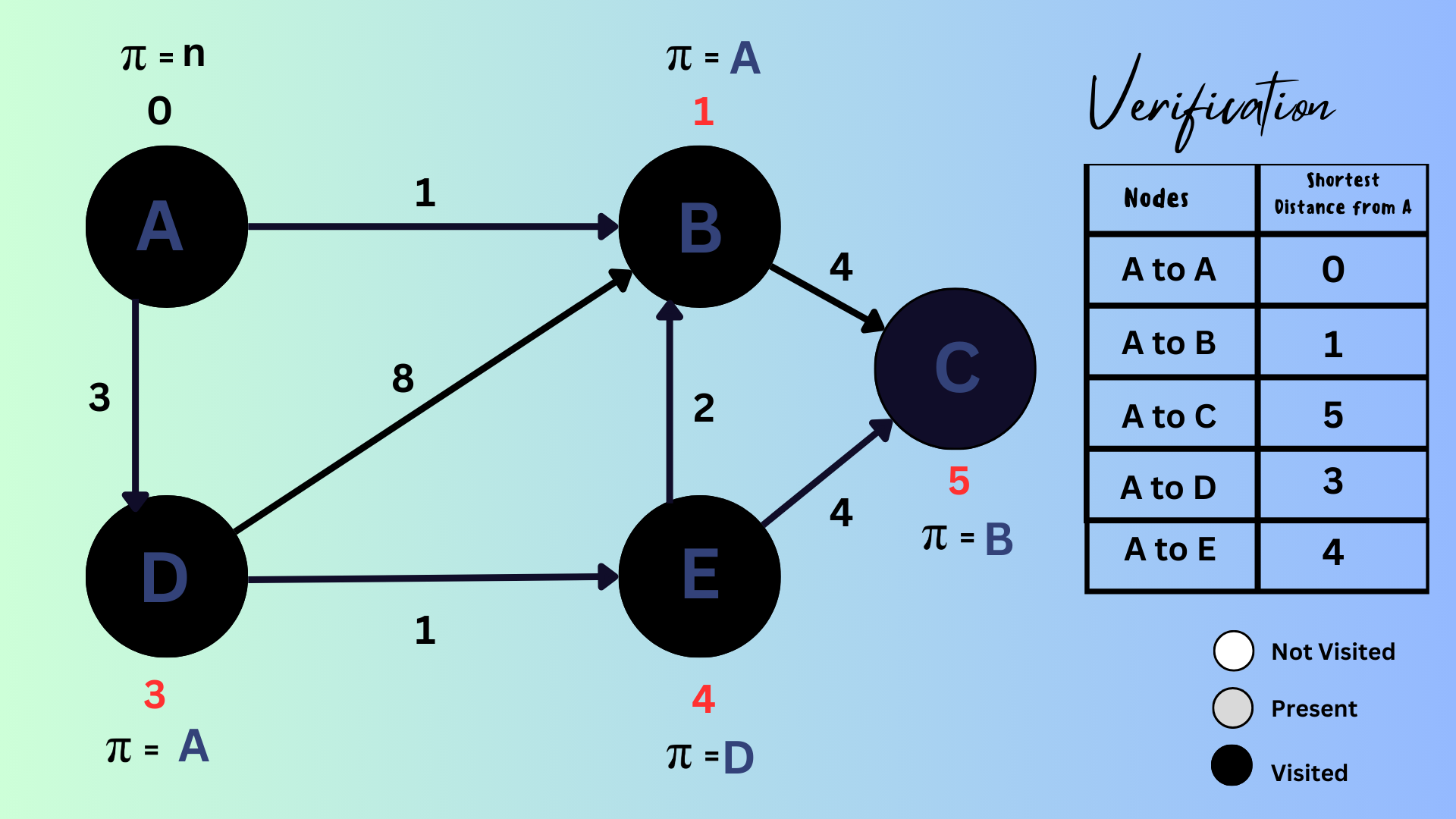
STEP-7: Verification of Dijkstra's Algorithm:

Let's verify our work!

Edge Weights and Path Calculation:

As we go over from A to A path, we already know its distance from itself will be zero.

1. From A to B: Direct edge with weight 1.

2. From A to C: The shortest path is A → B → C, with the total distance being 1 (A to B) + 4 (B to C) = 5.

3. From A to D: Direct edge with weight 3.

4. From A to E: The shortest path is A → D → E, with the total distance being 3 (A to D) + 1 (D to E) = 4.

---

Advantages of Dijkstra's Algorithm

• Efficiency: With a time complexity of O((V + E) log V), Dijkstra’s Algorithm is efficient for large graphs.

• Correctness: It guarantees the shortest path in graphs with non-negative weights.

• Versatility: Can be used in various applications, from network routing to geographical mapping.

---

Disadvantages of Dijkstra's Algorithm

• Dijkstra's Algorithm does not work correctly with graphs that have negative weight edges.

• Although efficient, the performance can degrade with extremely large graphs or dense graphs.

---

Conclusion

Dijkstra's Algorithm is a powerful tool for finding the shortest paths in graphs with non-negative weights. Its efficiency and correctness make it suitable for a variety of applications, from routing in navigation systems to optimizing network paths. Thus, understanding Dijkstra’s Algorithm and its implementation can enhance your problem-solving skills and open doors to more advanced topics in graph theory and algorithm design.