LLM Quantization

What is Quantization?

It is the process of reducing/mapping higher precision weights and activations into lower precision. In simple terms shrinking a model to smaller size that can be used to run on resources with limited memory.

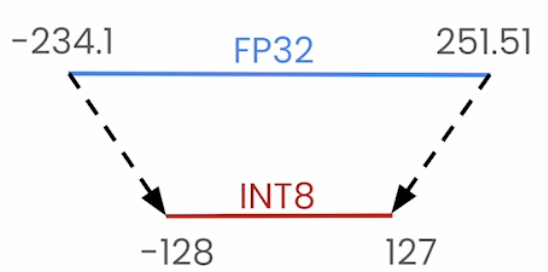
Linear Quantization?

Uses a linear mapping to map the higher precision to lower precision value ex:- FP32 - INT8

Formula for linear quantization

$$q = \text{int}\left(\text{round}\left(z + \frac{r}{\text{s}}\right)\right)$$

r => original tensor
s => scale[stored in the orignal tensor datatype]
q => quantized tensor
z => zero type[stored in the quantized tensor datatype]

How to determine the values of scale and zero point?

$$Scale = \frac{r_{max} - r_{min}}{q_{max} - q_{min}}$$

$$Zero Point = \text{int}\left(\text{round}\left(q_{min} - \frac{r_{min}}{\text{scale}}\right)\right)$$

If zero point is out of range, we can clip it example

if Z < q(min) then z = q(min)

if Z > q(max) then z = q(max)

for detailed derivation click the link: Detailed derivation

Modes in linear quantization

Asymmetric:- The derivation is same as the above
Symmetric:- In the symmetric mode we map the [-r(max), r(max)] to [-q(max), q(max)] we do not need the zero point, since it is zero.

$$Scale = \frac{r_{max}}{q_{max}}$$

$$Zero Point = 0$$

$$q = \text{int}\left(\text{round}\left(\frac{r}{\text{s}}\right)\right)$$

import torch
original_tensor=torch.tensor(
    [[191.6, -13.5, 728.6],
     [92.14, 295.5,  -184],
     [0,     684.6, 245.5]]
)
print(original_tensor.dtype)

torch.float32
# The original tensor is of type FP32 our goal is to convert it into int8

# The below function return the scale and the zero point of asymmetric mode.
def scale_zero_point(orginal_tensor, dtype=torch.int8):

    q_min, q_max = torch.iinfo(dtype).min, torch.iinfo(dtype).max
    r_min, r_max = orginal_tensor.min().item(), orginal_tensor.max().item()

    scale = (r_max - r_min) / (q_max - q_min)

    zero_point = q_min - (r_min / scale)

    if zero_point < q_min:
        zero_point = q_min
    elif zero_point > q_max:
        zero_point = q_max
    else:
        zero_point = int(round(zero_point))

    return scale, zero_point

# Once we get the scale and zero point from scale_zero_point function we can use them to pass through
# the linear_quantization function which outputs a quantized tensor.
def linear_quantization(
    orginal_tensor, scale, zero_point, dtype = torch.int8):

    intermediate_step = orginal_tensor / scale + zero_point # here we are just calculating the ((r/s) + z)

    rounded_tensor = torch.round(intermediate_step) # rounding the tensor

    q_min = torch.iinfo(dtype).min
    q_max = torch.iinfo(dtype).max

    q_tensor = rounded_tensor.clamp(q_min,q_max).to(dtype)

    return q_tensor

scale, zero_point = scale_zero_point(original_tensor)
print(scale," ",zero_point)

3.578823433670343   -77

quantized_tensor = linear_quantization(original_tensor, 
                    scale, zero_point)
quantized_tensor

tensor([[ -23,  -81,  127],
        [ -51,    6, -128],
        [ -77,  114,   -8]], dtype=torch.int8)

We have now perfectly quantized a float32 original tensor to int8 quantized_tensor.
Now that we have quantized the original tensor, we will now dequantize the quantized_tensor.

Dequantization

It is the process of converting the quantized_tensor to the original tensor

def linear_dequantization(quantized_tensor, scale, zero_point):
    return scale * (quantized_tensor.float() - zero_point)

The formula for dequantization is fairly simple

$$r = s \cdot (q - z)$$

dequantized_tensor = linear_dequantization(
    quantized_tensor, scale, zero_point)
dequantized_tensor

tensor([[ 193.2565,  -14.3153,  730.0800],
        [  93.0494,  297.0423, -182.5200],
        [   0.0000,  683.5552,  246.9388]])

The dequantized tensor and the original tensor looks almost the same, but there are discrepancies. The difference is called as quantization error.

Quantization error

It is the average squared difference between the original values and the quantized values.

It’s like saving a high-quality photo as a low-resolution one. The image might still look the same overall, but some fine details are lost, and that’s the "quantization error".

quant_error = original_tensor - dequantized_tensor
quant_error.square().mean()

1.5729731321334839

Thanks for reading until now, this blog is just an introduction to what quantization is but there are many other methods to do it. There are different granularities where quantization can be applied for example

Per Tensor:- This blog covered only this per tensor quantization since we have used the same scale and zero point on the whole tensor.
Per Channel:- This can be applying quantization for each row or column
ex:- using different scale and zero points on each row or column.
Per Group:- We define the group size and each group will have different scales and zero points.

The main goal is to reduce the error. In the next blog will cover different methods other than expansion.

References

https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-quantization#%C2%A7calibration
Huggingface Course:- Quantization in Depth

Getting Started with Quantization

Table of contents