Word Search

Problem

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

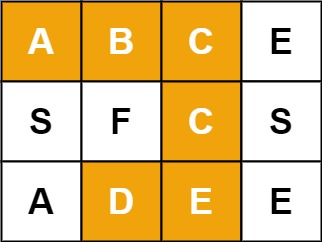
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

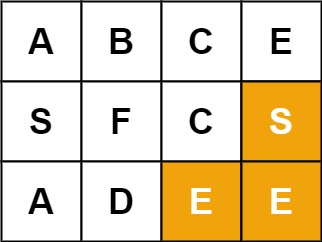
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m == board.length

• n = board[i].length

• 1 <= m, n <= 6

• 1 <= word.length <= 15

• board and word consists of only lowercase and uppercase English letters.

Solution

Recursive Approach (DFS)

The approach involves selecting an index (i, j) and checking if it’s possible to form a word starting with the letter at board[i][j]. We try all elements of the board as the starting letter to see which one forms the desired word.

Each time we check a letter, we verify if the current board[i][j] matches the corresponding letter in the given word. If it doesn’t, we immediately return false. The pointer that keeps track of the given word is index, which we increment by 1 whenever we check the next letter on the board.

If the current board[i][j] matches, we proceed to check the next letter in all four directions. If any direction returns true, we immediately return true without further checks. If all four directions fail, we return false.

Additionally, while on the (i, j) element, we maintain a separate matrix to track whether it has been visited. If we encounter an already visited element, we stop and return false.

Additionally, if the position (i,j) on the board is out of the given size, we return false.

class Solution {
    public boolean check(char[][] board, String word, int i, int j, String currentWord, boolean[][] visited, int index){

        if(word.equals(currentWord)) return true;

        if(i<0 || i>=board.length || j<0 || j>=board[0].length || 
        visited[i][j] || word.charAt(index)!=board[i][j]) return false;

        visited[i][j] = true;
        if(check(board, word, i, j+1, currentWord+board[i][j],visited, index+1) ||
        check(board, word, i+1, j, currentWord+board[i][j],visited, index+1) ||
        check(board, word, i, j-1, currentWord+board[i][j],visited, index+1) ||
        check(board, word, i-1, j, currentWord+board[i][j],visited, index+1)) return true;

        visited[i][j] = false;
        return false;
    }
    public boolean exist(char[][] board, String word) {
        boolean visited[][] = new boolean[board.length][board[0].length];
        for(int i = 0; i<board.length; i++){
            for(int j=0; j<board[0].length; j++){
                if(check(board, word, i, j, "",visited,0)) return true;
            }
        }
        return false;
    }
}

Time and Space Complexity

L - Length of the word

Time

O(nxm) x O(3^L)

We iterate over each element as the starting letter, resulting in O(nxm). From each element, there are 4 possible directions, but effectively 3 or fewer since the caller is on the neighbouring element or if the caller is on the first/last column or row. As we progress through the word index by index, the maximum number of elements we touch is (L) hence there will 3^L possibilities.

Space

O(nxm) + O(L)

We store the visited matrix, which O(nxm), and the maximum stack trace it can take up is O(L), corresponding to the length of the word.