Part 5: A Better Second Run
 Greg Alt
Greg Alt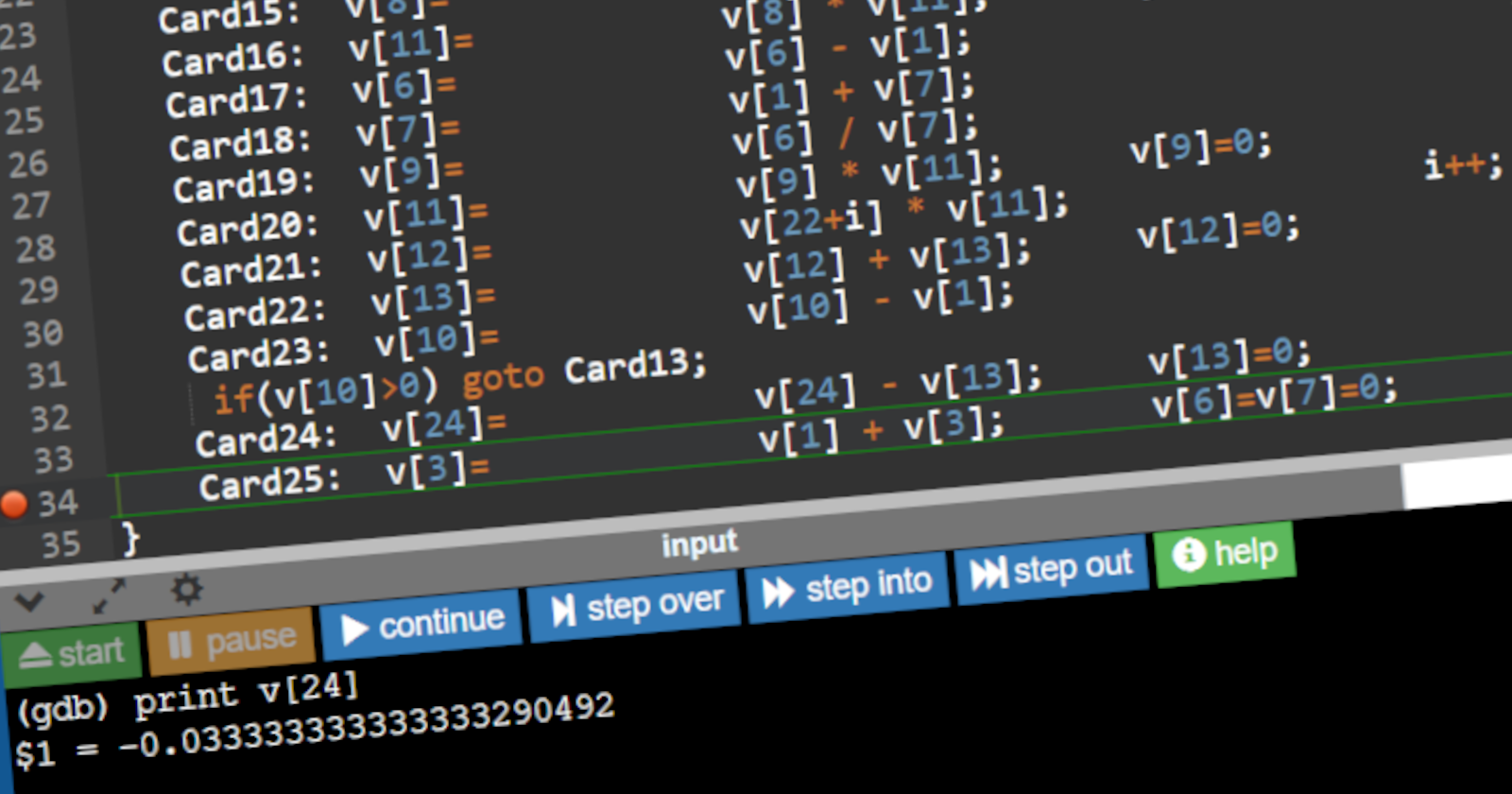
This is the fifth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program
In my last post, I tried a first run of Lovelace's program. Unfortunately, it generated the wrong value for B7. In my rush to run the program, I got ahead of myself. The C code I compiled and ran was a transliteration of a simple digital transcription of Lovelace's original published table. Clearly I missed something in that process.
Transcription, Transliteration, Translation…
As a first step in debugging this program, I'll look at that transcription and transliteration process, starting with a review of what I mean by those terms.
Transcription: a straightforward copying from one medium to another. When I transcribed Lovelace’s table program from a pixel-based image of the published table to a text-based digital spreadsheet, the goal was a table that contained all of the information in the original and that even appeared as identical as possible. Care was taken to avoid any additions, omissions, or modifications.
Transliteration: a dumb conversion from one set of text to another, moving or substituting symbols according to very simple rules. This has been my goal for converting between the spreadsheet format and compilable C code. I strove for as little semantic interpretation of the text as possible.
Translation: typically, a compiler parses source code in a high level language and then based on a semantic understanding of the code, translates to generate code in a lower-level language that accomplishes the same effect. This requires much more than simple text substitution.
As an analogy, if I start with the text, “Hello, World!” I can:
transcribe that to plain text, “Hello, World!”
transliterate it into pig-latin, “Ellohay, Orldway!”
or translate into French, “Bonjour le monde!”
Transliterating to C
To transliterate to C requires conversion of just the first five functional columns plus the sixth for an end of line comment. You can see how this transliteration is a simpler conversion than generally implied by compile or translate:
1st: simply becomes a label:
- | 16 | → Card16:
2nd through 4th: the simple two operand arithmetic operation with one or more destination variables for the result. The upper left indices can be ignored for this transliteration:
- | * | 1v8 * 3v11 | 4v11 | → v[11] = v[8] * v[11];
5th: any variable listed with a 0 as the upper left index on the right-hand side of the equals sign is reset to zero:
- | { 1v8 = 0v8, 3v11 = 4v11 } | → v[8] = 0;
6th: the end of line comment is added:
- | = 2n/2 * (2n-1)/3 | → // = 2n/2 * (2n-1)/3
I’ll talk more later about the fifth column and the need to explicitly reset variables to zero. For now, just remember that simply overwriting a non-zero variable is a modern concept not supported by the Analytical Engine. This is due to the complexity of mechanically turning a base 10 gear to the correct amount.
Altogether, here's the less familiar original notation from the transcription:
| 16 | * | 1v8 * 3v11 | 4v11 | { 1v8 = 0v8, 3v11 = 4v11 } | = 2n/2 * (2n-1)/3 |
Through trivial text substitution rules, this becomes the more familiar C code:
Card16: v[11] = v[8] * v[11]; v[8] = 0; // = 2n/2 (2n-1)/3
I implemented these conversions as simple text substitution functions in the spreadsheet. While this simple automatic transliteration turns the 25 numbered rows into valid C code, it is missing a few pieces from the table, and some additional C boilerplate required to compile.
Some Boilerplate
I added this standard C boilerplate, along with a closing curly brace at the end:
int main() {
Then I added a couple lines to declare the variables and assign the values listed in the table’s header. Note that the variables v[21] through v[23] won't need to be explicitly set once we get things working "from the very beginning":
long double v[100] = { 0 };
v[1]= 1; // [1]
v[2]= 2; // [2]
v[3]= 4; // [n]
v[21] = 1.0/6.0; // [B1]
v[22] = -1.0/30.0; // [B3]
v[23] = 1.0/42.0; // [B5]
But more needs to be done because when we run it, we get the wrong answer. Instead of v[24] being loaded with -0.03333…, the correct value for B7, we get -0.442857142857142887659.
Some Things Missed in the First Run
While I can't directly pair debug this with Ada Lovelace, I will do the next best thing and read what she has written to get better insights into the code. She wrote extensively in the text of Note G, giving the equivalent of almost line by line modern block comments as well as more general commentary on her intent with the program. In addition, the table itself has the equivalent of end of line comments for each operation, plus a table to the right showing a view of the expected value of each variable after each operation. Together, this is a wealth of information to draw from—close to a true pair debugging experience.
First off, I forgot to fix the typo in operation 4 in the original table. Remember, that to match the comment, it should be v4 / v5 and not the other way around.
Card4: v[11]= v[4] / v[5]; v[5]=v[4]=0; // = (2n-1)/(2n+1)
The Inner Loop
There are a couple other missing pieces that I glossed over. For one, my transliteration completely ignored the loop specified in the table with
Here follows a repetition of Operations thirteen to twenty-three.
Clearly this should be converted to a simple conditional jump:
if (...) goto Card13;
That raises the question, what condition should be used here? Let’s consult with Lovelace. In talking about the uses of different variables, she explains:
V10 always decides which of two courses the succeeding processes are to follow, by feeling for the value of n through means of a subtraction.
We can see that V10 is decremented each iteration of the loop in Operation 23 and she makes clear that the loop terminates specifically when V10 reaches 0:
At the termination of the repetition of operations (13…23) [...] the alterations in the values on the Variables are, that [...] V10 = 0.
This is fascinating because this style of loop was rediscovered in the 20th century. As I mentioned in a previous post, the pattern of subtracting one and conditionally branching for a loop, terminating on zero, is so common that many twentieth century architectures included a single complex instruction to do all of that. Examples include Z80’s DJNZ, PDP-11’s SOB, and x86’s LOOP instruction.
If you've written assembly language on modern CPUs, you're probably spoiled with the variety of conditionals available. It wasn't always like that. For example, only one type of conditional jump was supported in the first assembly language, described in Kathleen Booth’s 1947 “Coding for A.R.C.” It was similar to the one Lovelace uses, though it terminated on -1 instead of 0.
Booth's assembly language supported statements of the form, “Cc C to M(+n)”, which means “if number in A >= 0 shift control to M” with n specifying the relative offset. If A is negative, then there is no jump. Execution proceeds to the next instruction. The condition is assumed to always be A >= 0.
In discussing the choice of the single conditional branch instruction Booth stated:
“The inclusion of a conditional transfer order is also well justified from the above points of view, the exact specification of its nature is, however, more speculative”.
In 1842, Babbage made what is thought to be the first mention of user-programmable conditional branching.1 This was later included in an 1845 notebook, where Babbage listed a full working instruction set for the Analytical Engine, including the “small operations” such as “Ascertaining if a variable = 0,” which provides a conditional branch if the variable is zero.2 Additionally, a table that Babbage made in 1838 appears to show a horizontal bar notation for conditional branches. The table doesn't show variables used, so it can't be considered a program, but it appears to be a clear investigation of conditional branching to determine the time required to make a complex calculation.3
While the exact details of the hardware itself are unclear, the language of the table is clear. A way to support this in my transliteration while keeping the C code straightforward is to just compare the last-used destination variable with zero. Operation 23 and the “Here follows a repetition” statement become:
Card23: v[10]= v[10] - v[1]; // = n-3 (=1)
if (v[10] > 0) goto Card13;
This is possible if the transliteration simply replaces “Here follows a repetition of Operations” with “if ([...] > 0) goto Card” and “thirteen to twenty-three” with “13;” And finally, a substitution that goes a bit beyond dumb transliteration–place the destination variable from the previous operation into the conditional.
Does it Work Yet?
It is tempting to try running things again, but, unfortunately, we get another wrong answer, B7 = -0.5 instead of -0.03333…
Consulting with Lovelace again, she points out that:
Operation 21 always requiring its factor from a column one in advance of that which it used the previous time
What does that mean and how do we adjust the code or transliteration to match this intent?
Variable Indexing
Her handling of variable indexing is interesting. In the course of crafting the program to compute the Bernoulli numbers, she encountered a problem that hadn’t been exposed in previous trivial examples. In 1843, Babbage’s work-in-progress design of the Analytical Engine’s hardware did not support programmatically reading or writing to variables in a series. She saw the need to extend this design and wrote her code assuming this extension.
Calculating each Bernoulli number required iterating over all previous ones, and then placing the newly calculated value at the end of the series. This process would then be repeated, extending the series indefinitely. She saw the importance of adding this indexing feature and raised the issue with Babbage in private letters. Not wanting to draw attention to gaps in the evolving hardware design, she handled this “diplomatically” by precisely explaining the software specification she used while leaving the discussion of hardware to just that it would be “easily provided for”:
The only exception to a perfect identity in all the processes and columns used, for every repetition of Operations (13…23), is that Operation 21 always requires one of its factors from a new column, and Operation 24 always puts its result on a new column. But as these variations follow the same law at each repetition (Operation 21 always requiring its factor from a column one in advance of that which it used the previous time, and Operation 24 always putting its result on the column one in advance of that which received the previous result), they are easily provided for in arranging the recurring group (or cycle) of Variable-cards.
Babbage agreed that she was right. Later, in 1859, he privately wrote more about it, suggesting he had incorporated the idea into his evolving design:4
11 Feb 1859 It appears that in the solution of n simple equations the indices of the Variable may be so chosen that they shall follow an arithmetical law. But whenever such indices follow such a law then of course the engine can easily calculate the law and thus by conveying the numbers calculated directly to the apparatus which selects the variable do away with any necessity for cards.
A century later, when computers were actually built in the 1940s, they also initially lacked index registers. For a few years, programmers used self-modifying code as a work-around to read/write data in series. This changed with the Manchester Mark I in 1949, the first to add the now ubiquitous index register feature.5
It’s worth noting that the program in Note G doesn’t require fully random access indexing. A much more limited, simple auto-increment addressing mode is sufficient. In 1953, the “Speedcoding” system for the IBM 701 was developed that supported a primitive auto-increment addressing mode to support computing with arrays of data.
It is fascinating that in both the 1840s and 1940s, only when programmers tried to do something nontrivial did they push the hardware design to add proper support for both array indexing and conditional branching. Programmers now take these two features for granted, but they were far from obvious before the 1950s.
Following the intent laid out in Note G, Operation 21 becomes:
Card21: v[12]= v[22+i] * v[11]; i++;
Let’s try it out and see if that fixes things…
OK, Does it Work Now?
Running again gives us the correct magnitude but wrong sign:
B7 = 0.0333333333333333
A careful reading of the table shows a second bug. The comment makes it clear that v24 should be assigned B7, not -B7. But going back to the original math, equation (9.) shows the source of the error. Doing the next step to solve for B2n-1 means that the rest must be negated:
0 = A0 + A1B1 + A3B3 + A5B5 + ... + B2n-1 (9.)
This appears to not be a simple typesetting error, but an actual bug from when Lovelace translated the math into code, missing the negation. She makes the same mistake in her Note G description of the code, "transfer the value which is on V13 to V24" The fix, though, is simple and straightforward. Modify Operation 24 to subtract v13 from v24, not add:
| 24 | + | 4v13 + 0v24 | 1v24 | { 4v13=0v13, 0v24=1v24 } | = B7 |
becomes:
| 24 | - | 0v24 - 4v13 | 1v24 | { 4v13=0v13, 0v24=1v24 } | = B7 |
And the transliterated C code becomes:
Card24: v[24]= v[24] - v[13]; v[13]=0; // = B7
OK, this Should Work, Right?
OK, here's the updated C code with everything from above:
int main() { long double v[100] = { 0 };
v[1]= 1; // [1]
v[2]= 2; // [2]
v[3]= 4; // [n]
v[21] = 1.0/6.0; // [B1]
v[22] = -1.0/30.0; // [B3]
v[23] = 1.0/42.0; // [B5]
int i=0;
Card1: v[4]=v[5]=v[6]= v[2] * v[3]; // = 2n
Card2: v[4]= v[4] - v[1]; // = 2n-1
Card3: v[5]= v[5] + v[1]; // = 2n+1
Card4: v[11]= v[4] / v[5]; v[5]=v[4]=0; // = (2n-1)/(2n+1)
Card5: v[11]= v[11] / v[2]; // = 1/2*(2n-1)/(2n+1)
Card6: v[13]= v[13] - v[11]; v[11]=0; // = -1/2*(2n-1)/(2n+1) = A0
Card7: v[10]= v[3] - v[1]; // = n-1 (=3)
Card8: v[7]= v[2] + v[7]; // = 2+0 = 2
Card9: v[11]= v[6] / v[7]; // = 2n/2 = A1
Card10: v[12]= v[21] * v[11]; // = B1*2n/2 = B1A1
Card11: v[13]= v[12] + v[13]; v[12]=0; // = -1/2*(2n-1)/(2n+1)+B1*2n/2
Card12: v[10]= v[10] - v[1]; // = n-2 (=2)
Card13: v[6]= v[6] - v[1]; // = 2n-1
Card14: v[7]= v[1] + v[7]; // = 2+1 = 3
Card15: v[8]= v[6] / v[7]; // = (2n-1)/3
Card16: v[11]= v[8] * v[11]; v[8]=0; // = 2n/2*(2n-1)/3
Card17: v[6]= v[6] - v[1]; // = 2n-2
Card18: v[7]= v[1] + v[7]; // = 3+1 = 4
Card19: v[9]= v[6] / v[7]; // = (2n-2)/4
Card20: v[11]= v[9] * v[11]; v[9]=0; // = 2n/2*(2n-1)/3*(2n-2)/4 = A3
Card21: v[12]= v[22+i] * v[11]; i++; // = B3*2n/2*(2n-1)/3*(2n-2)/3 = B3A3
Card22: v[13]= v[12] + v[13]; v[12]=0; // = A0 + B1A1 + B3A3
Card23: v[10]= v[10] - v[1]; // = n-3 (=1)
if(v[10]>0) goto Card13;
Card24: v[24]= v[24] - v[13]; v[13]=0; // = B7
Card25: v[3]= v[1] + v[3]; v[6]=v[7]=0; // = n+1 = 4+1 = 5; by a Variable-card. by a Variable card.
}
And sure enough… running again, we get the correct answer:
B7 = -0.0333333333333333
This is worth celebrating, but Lovelace is already shaking her head.
At this point we have a complex program that does useful work, as Lovelace describes:
the computation for B7 (B1, B3, B5 being supposed given).
This is certainly interesting, but it is not Lovelace’s full intent for the program. Considering this result, she remarks:
It is true that if we consider our computation of B7 as a perfectly isolated calculation, we may conclude B1, B3, B5 to have been arbitrarily placed on the columns; [...] But we are not taking this view. On the contrary, we suppose the engine to be in the course of computing the Numbers to an indefinite extent, from the very beginning;
Fortunately, we are getting close to that goal.
In my next blog post, I'll consult deeper with Lovelace's commentary in Note G to get her program computing to an indefinite extent.
“The first evidence of user-programmable conditional branching appears in an entry dated 19 March 1842 in what Babbage called the 'minor operations' – ascertaining if a variable is zero, and ascertaining if a variable is + or -." Plan 28 Blog, Autumn 2017 report to the Computer Conservation Society
A. G. Bromley, "Babbage's Analytical Engine Plans 28 and 28a. The programmer's interface," in IEEE Annals of the History of Computing, vol. 22, no. 4, pp. 5-19, Oct.-Dec. 2000
"Use of combinatorial cards in the computation of the coefficients in the product of two polynomials," BAB/L/023, The Babbage Papers at the Science Museum, London.
Cambridge sketchbook from Feb. 11, 1859, p.295. comment from Tim Robinson
"Programming the Mark I: Early Programming Activity at the University of Manchester," Martin Campbell-Kelly. Annals of the History of Computing, April, 1980. p135
Subscribe to my newsletter
Read articles from Greg Alt directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
