Introduction to Vector Databases: How They Work and Why They Matter

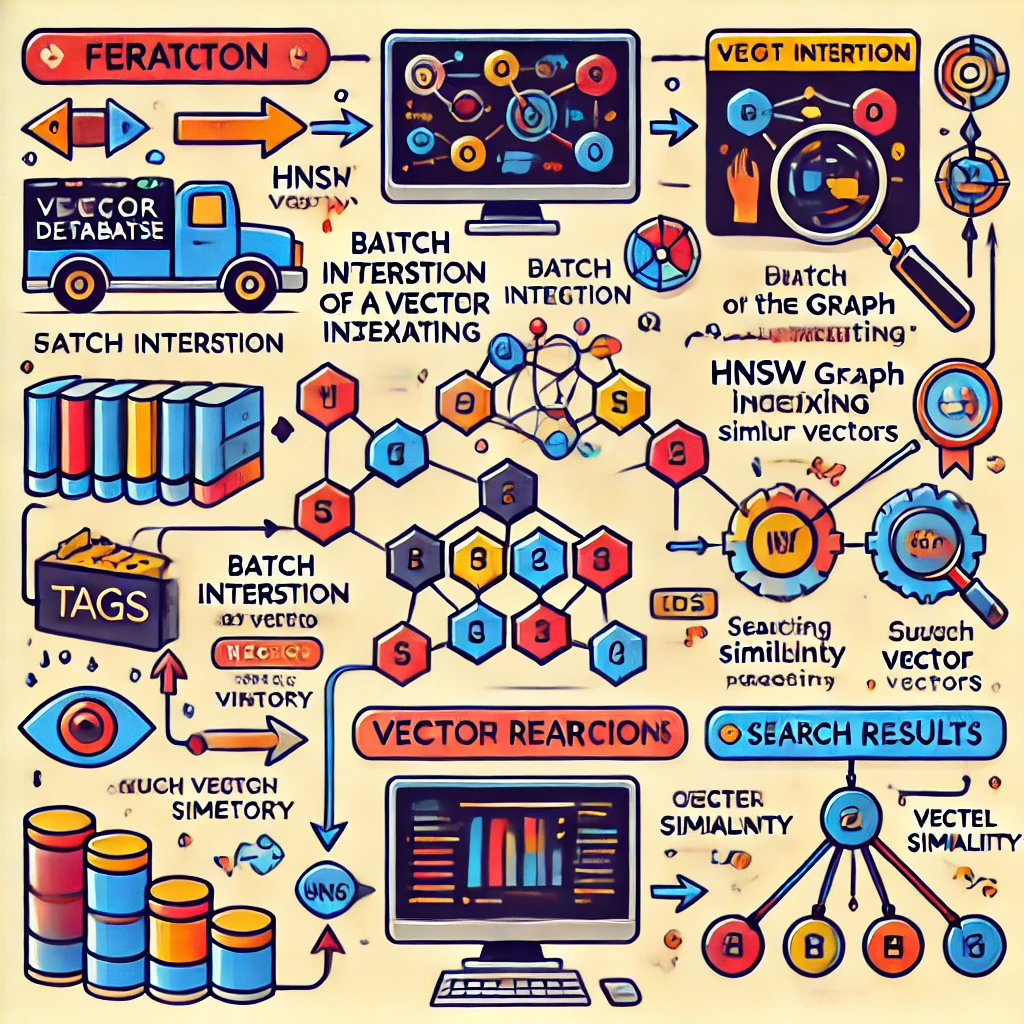
What is Vector Database

A vector database is a collection of data stored as mathematical representations. Vector databases make it easier for machine learning models to remember previous inputs, allowing machine learning to be used to power search, recommendations, and text generation use cases. Data can be identified based on similarity metrics instead of exact matches, making it possible for a computer model to understand data contextually.

When one visits a shoe store, a salesperson may suggest shoes that are similar to the pair one prefers. Likewise, when shopping in an ecommerce store, the store may suggest similar items under a header like "Customers also bought..." Vector databases enable machine learning models to identify similar objects, just as the salesperson can find comparable shoes and the e-commerce store can suggest related products. (In fact, the e-commerce store may use such a machine learning model for doing so.)

To summarize, vector databases allow computer programs to draw comparisons, identify relationships, and understand context*.* This enables the creation of advanced artificial intelligence (AI) programs like large language models (LLMs).

So what does a vector look like? Vector is an array of numerical values eg: [1, -6, 8.3, 0]

How Vector Databases Work

Vector databases employ a combination of specialized indexing, querying, and similarity search techniques to efficiently store vectors and enable fast, scalable, and accurate retrieval of the most similar vectors to a given query.

We can sort numerical data and index them. For text, we have Lucene indexing. so how do we store Vectors? and what index do we need to do to enable faster searches and what are the tradeoffs:

below are a few approaches to index vectors Hashing, Graph-based, and Quantization

• Hashing

• Algorithms like Locality-Sensitive Hashing (LSH) map similar vectors into the same "buckets" or "bins" so that they can be quickly retrieved. Picture a giant game of Sudoku, where each hash bucket is a subgrid containing similar vectors. When a query vector comes in, it gets hashed to a bucket and only needs to be compared to the other vectors in that same bucket. Lets take a mathematical example for this:

  • Step1: Lets consider 3 vectors that need to be stored, By looking at them we can say v1 and v2 are very close

    • v1​=[1,2,3]

    • v2=[1.1,2.1,3.1]

    • v3=[4,5,6]

  • Step2: Consider a hash function, here for simplicity let's consider a hyperplane-based hash function

    • hash vector: r=[0.3,−0.1,0.5]

  • Step 3: Compute Hash Values Let’s compute the dot products:

    • For v1=[1,2,3] the dot product with r is 1(0.3)+2(−0.1)+3(0.5)=0.3−0.2+1.5=1.6. Since this is positive, we assign v1​ to bucket 1.

    • For v2=[1.1,2.1,3.1] the dot product with r is 1.1(0.3)+2.1(−0.1)+3.1(0.5)=0.33−0.21+1.55=1.67. This is also positive, so v2 is assigned to bucket 1.

    • For v3=[4,5,6], the dot product with r is 4(0.3)+5(−0.1)+6(0.5)=1.2−0.5+3=3.7. This is also positive, so v3 is assigned to bucket 1.

  • In this simple example, all vectors ended up in the same bucket, but with more hash functions and different random projections, similar vectors would consistently cluster together across different hash values.

  • The key idea behind LSH is to use hash functions that map similar data points (according to some distance metric) to the same buckets with a higher probability than dissimilar points. LSH is typically used for tasks like:

    • Approximate nearest neighbor search

    • Finding similar documents or images

    • Clustering

  • Here’s a basic example with Python’s datasketch library for LSH:

      pythonCopy codefrom datasketch import MinHash, MinHashLSH
      import numpy as np
    
      # Create MinHash signatures (a type of LSH)
      num_elements = 10000
      dim = 128
    
      # Generate random data points
      data = np.random.randn(num_elements, dim).astype('float32')
    
      # Initialize LSH with parameters
      lsh = MinHashLSH(threshold=0.8, num_perm=128)
    
      # Hash each vector
      for i, vec in enumerate(data):
          m = MinHash(num_perm=128)
          for val in vec:
              m.update(str(val).encode('utf8'))
          lsh.insert(f"vec_{i}", m)
    
      # Querying the LSH index
      query_vec = np.random.randn(1, dim).astype('float32')
      m_query = MinHash(num_perm=128)
      for val in query_vec[0]:
          m_query.update(str(val).encode('utf8'))
    
      # Retrieve similar items
      result = lsh.query(m_query)
      print(result)
    

    How to Determine the Number of Buckets in LSH

    To determine the number of buckets in LSH, we need to consider two parameters:

    1. Number of Hash Functions (L): This defines how many different hash functions we use to generate multiple hash tables. The higher the number of hash functions, the more precise the search (but slower). num_perm in above example

    2. Number of Hash Tables (k): This determines how many times we hash the same data with different random vectors. Increasing k generally leads to higher accuracy but can increase memory usage and slightly decrease the speed.

The trade-off: More buckets (from increasing k) will improve the ability to discriminate between close and distant points but might result in too many buckets with few points. On the other hand, fewer buckets (smaller k) could lead to many points in the same bucket, which increases the number of points to check during the search.

Calculating the Number of Buckets (Optimal Parameters)

To find the optimal number of buckets, you need to balance:

• Recall: How many of the actual nearest neighbors are retrieved.

• Precision: How often the retrieved neighbors are actually correct.

• Speed: How quickly the search can be completed.

You typically need to experiment with the following:

• Bucket Size: Smaller bucket sizes might lead to more precision but slower performance (more false positives to check).

• L and k values: You can choose L and k empirically based on your dataset.

• Graph-based

• HNSW is a graph-based ANN method that builds a multi-layered graph where each node represents a data point (vector). It forms links between the nodes based on proximity, creating a graph with "shortcuts" between close points. This makes it faster to navigate through the graph and find approximate nearest neighbors, a step-by-step approach to how it works

  • Graph Construction: HNSW builds layers of proximity graphs. Each layer has a set of nodes and edges where the edges connect nodes that are close in the metric space. Higher layers contain a sparser graph (fewer nodes), while lower layers are denser with more nodes.

    • Let’s take a small set of vectors as we did earlier:

      • v1=[1,2]

      • v2=[2,3]

      • v3=[4,4]

      • v4=[5,5]

      • v5=[6,7]

      • v6=[7,8]

    • HNSW constructs a multi-layer graph:

      • Upper layers: Fewer points, with long-range connections. These help in quickly navigating to the general area of interest in the search space.

      • Lower layers: Denser connections between nearby points, used to refine the search once you are in the right vicinity.

For simplicity, let’s consider that we are building a two-layer HNSW:

• Layer 1 (Upper layer): Sparse, with long connections between points.

• Layer 0 (Lower layer): Denser connections, where nodes are connected to their nearest neighbors.

Here’s how the graph construction would look conceptually:

Layer 1 (Upper Layer) Connections:

• v1​ might be connected to v3.

• v3 might be connected to v5

These long-range connections help the algorithm make big leaps across the space to quickly get to a region near the query vector.

Layer 0 (Lower Layer) Connections:

• v1​ is connected to v2​ (because they are close).

• v2 is connected to v3

• v4 is connected to v5, and v5 is connected to v6

  • Search Process: When you perform a search, the algorithm starts at the top layer (which is the sparsest) and makes rough moves to get closer to the query vector. As it moves to lower, denser layers, it refines the search and finds more precise neighbors.

  • Now, let’s search for the nearest neighbor of a query vector q=[5.5,6].

• Start at Layer 1: Since this layer is sparse, the algorithm can quickly jump to relevant regions of the space. For example, it might start at v1​, then jump to v3, and then move to v5

• Move to Layer 0: Once the search reaches v5​ (which is close to the query vector), the algorithm moves down to Layer 0 to perform a finer search. Here, it refines the result by checking the neighbors of v5, which might lead it to v6, and finally identifies v5 and v6 as the nearest neighbors of the query vector.

  • Efficient Search: By building a hierarchical graph, HNSW can quickly navigate and prune large parts of the search space, significantly reducing the number of comparisons required for finding nearest neighbors.

  • Here’s how to use HNSW for ANN in Python with the hnswlib library:

  pythonCopy codeimport hnswlib
  import numpy as np
  
  # Number of elements
  num_elements = 10000
  
  # Dimensionality of the vectors
  dim = 128
  
  # Initialize HNSW index
  index = hnswlib.Index(space='l2', dim=dim)  # Use L2 distance
  
  # Randomly generate data (128-dimensional vectors)
  data = np.random.randn(num_elements, dim).astype('float32')
  
  # Initialize the index - maximum number of elements, and parameters
  index.init_index(max_elements=num_elements, ef_construction=200, M=16)
  
  # Add data to the index
  index.add_items(data)
  
  # Perform a search with a query
  query_vector = np.random.randn(1, dim).astype('float32')
  labels, distances = index.knn_query(query_vector, k=10)  # Find 10 nearest neighbors
  
  print(labels)
  print(distances)
  

  • Parameter Tuning in HNSW:

  • M: Controls the number of neighbors each node is connected to.

• Higher M values lead to more accurate searches but require more memory and slower index building.

• Lower M values reduce memory usage and construction time but decrease accuracy.

  • efSearch: The size of the dynamic candidate list during the query process.

• Higher efSearch increases accuracy at the cost of slower queries.

• Lower efSearch speeds up queries at the cost of lower accuracy.

  • ef_Construction: Controls the size of the dynamic list during graph construction.

• Higher ef_Construction builds a more accurate graph but increases construction time.

• Lower ef_Construction speeds up graph building but may reduce accuracy.

• The trade-off summary:

  • Accuracy vs. Speed: Tuning efSearch and M allows you to balance how much accuracy you want versus how quickly you want the search to be performed.

  • Memory Usage vs. Query Time: Larger graphs (higher M values) improve accuracy but increase memory consumption and slow down graph construction.

  • Graph Construction Time vs. Query Efficiency: Spending more time on graph construction (higher ef_Construction) leads to faster and more accurate queries but increases upfront costs.

• Quantization: Methods like Product Quantization (PQ) work by compressing vectors into compact representations. The original vectors are split into smaller subvectors, and each subvector is mapped to a short code based on its closest match in a codebook. Essentially, vectors are converted into a sequence of codes that can be efficiently stored and compared. To search, the query vector is also compressed and the database finds the vectors with the most similar code sequences. a step-by-step approach to how it works

• Vector Subdivision: If the original vector has 128 dimensions (d=128) and you decide to divide it into m=4 parts, each part will have d′= d/m=32 dimensions. now there are 4 sub-vectors and each has 32 dimensions

  • v=[v1​,v2​,…,v128​]

  • You divide it into 4 sub-vectors of 32 dimensions each:

    • v1(1)=[v1,v2,…,v32]

    • v2(1)=[v33,v34,…,v64]

    • v3(1)=[v65,v66,…,v96]

    • v4(1)=[v97,v98,…,v128]

Quantization:

• • For each sub-vector, PQ builds a codebook (a set of representative vectors) using clustering algorithms like k-means.

    • Each sub-vector is quantized to the nearest representative vector from the corresponding codebook.

    • For each sub-vector, you apply k-means to create 256 representative clusters (or codebook entries). When searching for the nearest neighbor, instead of comparing all vectors fully, you compare the query’s sub-vector against the precomputed codebooks.

• Compression:

  • After quantizing each sub-vector, the full vector is represented by the indices of the quantized sub-vectors. This drastically reduces the storage required.

  • If each sub-vector has 256 representative vectors in its codebook, you can store the entire vector as just 4 bytes (since each index is 1 byte).

• Approximate Nearest Neighbor Search:

  • During the search phase, you don’t need to compare all vectors fully.

  • Instead, for each query vector, you quantize it in the same way and compute distances between the query and dataset vectors by only using the precomputed codebook distances, which are much smaller.

  • Here’s how you can implement Product Quantization using the FAISS library, which is highly optimized for large-scale ANN search.

      pythonCopy codeimport faiss
      import numpy as np
    
      # Number of elements
      num_elements = 10000
    
      # Dimensionality of the vectors (128-dimensional vectors)
      dim = 128
    
      # Generate random data (128-dimensional vectors)
      data = np.random.randn(num_elements, dim).astype('float32')
    
      # Create the product quantizer (PQ)
      nlist = 100  # Number of Voronoi cells (centroids)
      m = 8        # Number of sub-vectors (subspaces), i.e., vector is split into 8 parts
      k = 256      # Number of codewords (clusters) in each sub-vector codebook
    
      # FAISS Index with Product Quantization
      index = faiss.IndexIVFPQ(faiss.IndexFlatL2(dim), dim, nlist, m, k)
    
      # Train the index with a subset of the data
      index.train(data)
    
      # Add data to the index
      index.add(data)
    
      # Perform a search with a query
      query_vector = np.random.randn(1, dim).astype('float32')
      k_nearest_neighbors = 10  # Number of nearest neighbors to retrieve
    
      distances, indices = index.search(query_vector, k_nearest_neighbors)
    
      print(f"Indices of nearest neighbors: {indices}")
      print(f"Distances to nearest neighbors: {distances}")
    

    Parameters in Product Quantization:

    • m (Number of Sub-Vectors):

      • The number of sub-vectors the full vector is split into. Increasing this value increases the precision of the quantization but requires more memory and computation.

    • k (Number of Clusters per Sub-Vector):

      • The number of codewords or clusters created in the codebook for each sub-vector. Larger values provide higher precision but also increase memory usage.

    • nlist (Number of Voronoi Cells):

      • The number of centroids used for partitioning the dataset during search. Larger values result in finer partitioning, improving accuracy but increasing memory consumption and training time.

• Trade-Offs:

  • Accuracy vs. Memory: PQ offers a trade-off between accuracy and memory usage. Compressing vectors with more sub-vectors (m) and codewords (k) increases accuracy, but it also increases memory consumption.

  • Speed vs. Precision: Increasing the number of codewords or sub-vectors can make the search slower due to more precise matching, but it provides better results.

After learning how vectors are stored and queried, there are often additional steps before delivering the final results to the user. The vector IDs are typically mapped back to the original data entries they represent. These results may be filtered, ranked, or aggregated based on associated metadata. For instance, when searching for similar images, the results could include metadata like titles, descriptions, or tags that can be used to refine the output.

By implementing this workflow, a vector database simplifies the process of storing, indexing, and searching vast unstructured datasets. It provides a straightforward query interface for finding similar items. As data and models scale, vector databases can deliver fast, relevant results without a proportional increase in compute and storage costs.

Conclusion

Vector databases represent a groundbreaking technology that leverages AI and machine learning to make the massive amounts of unstructured data generated today more easily searchable, analyzable, and actionable. By encoding complex data objects as high-dimensional vectors, they enable new possibilities for searching by semantic similarity, delivering intelligent recommendations, detecting anomalies, identifying patterns, and optimizing data management processes.

In this article, we’ve explored various aspects of vector databases, including their differences from traditional databases, the key components and workflows involved, powerful use cases, and the significant advantages they offer to organizations. This should provide you with a strong understanding of this innovative technology.

However, this is just the beginning of what vector databases can achieve. As the technology evolves and machine learning models advance, their applications will extend into exciting new areas. We are still in the early phases of this vector database revolution, and it’s likely they will become a core element of the modern data stack in the near future.