Q. The question goes like you are given N meetings with their start and end times, find the maximum number of meetings you can attend without any overlap.

Introduction:

It is one of the activity selection problem. Here, we gotta find maximum number of meetings one can attend, without overlapping.

Approach

We are applying greedy algorithm here . The core idea is to always select a meeting that ends early so that we can choose maximum number of meetings. Sorting the meetings with their end times will help us implement this strategy efficiently.

---

Step-by-Step Explanation

1. Input: We start by having two lists—one for start times and one for end times of the meetings.

2. Pair Meetings: First, we create pairs of start and end times for each meeting and store them along with their index.

3. Sort by End Time: Next, we sort the meetings by their end times. Sorting helps us easily find the earliest finishing meeting.

4. Greedy Selection: After sorting, we select the first meeting and then continue selecting meetings that start after the previous meeting ends.

5. Result: The result is a list of indices of the meetings that can be attended without any overlap.

   Code Implementation:

   

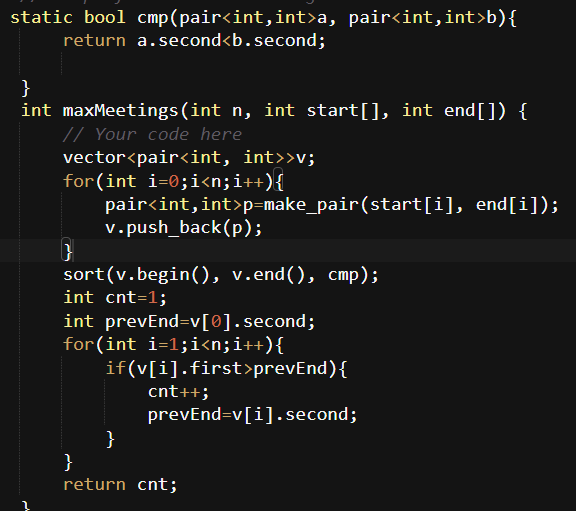
   Time Complexity Analysis

   1. Sorting: Sorting the meetings based on end times takes O(n log n).

   2. Iterating: After sorting, we iterate through the meetings once, which takes O(n).

Thus, the overall time complexity of this solution is O(n log n), where n is the number of meetings.

Space Complexity

The space complexity is O(n) since we store the meetings in a list of pairs, and we also store the result in an additional list.

Why did we use static for the comp function?

The static keyword restricts the function’s scope to the file it's defined in. This is useful when you don't need the function to be accessible from other parts of your program or project. It's often used to avoid naming conflicts in larger codebases where multiple files might have functions with the same name.