Arithmetic Expressions Evaluator: Part 2
 arman takmazyan
arman takmazyan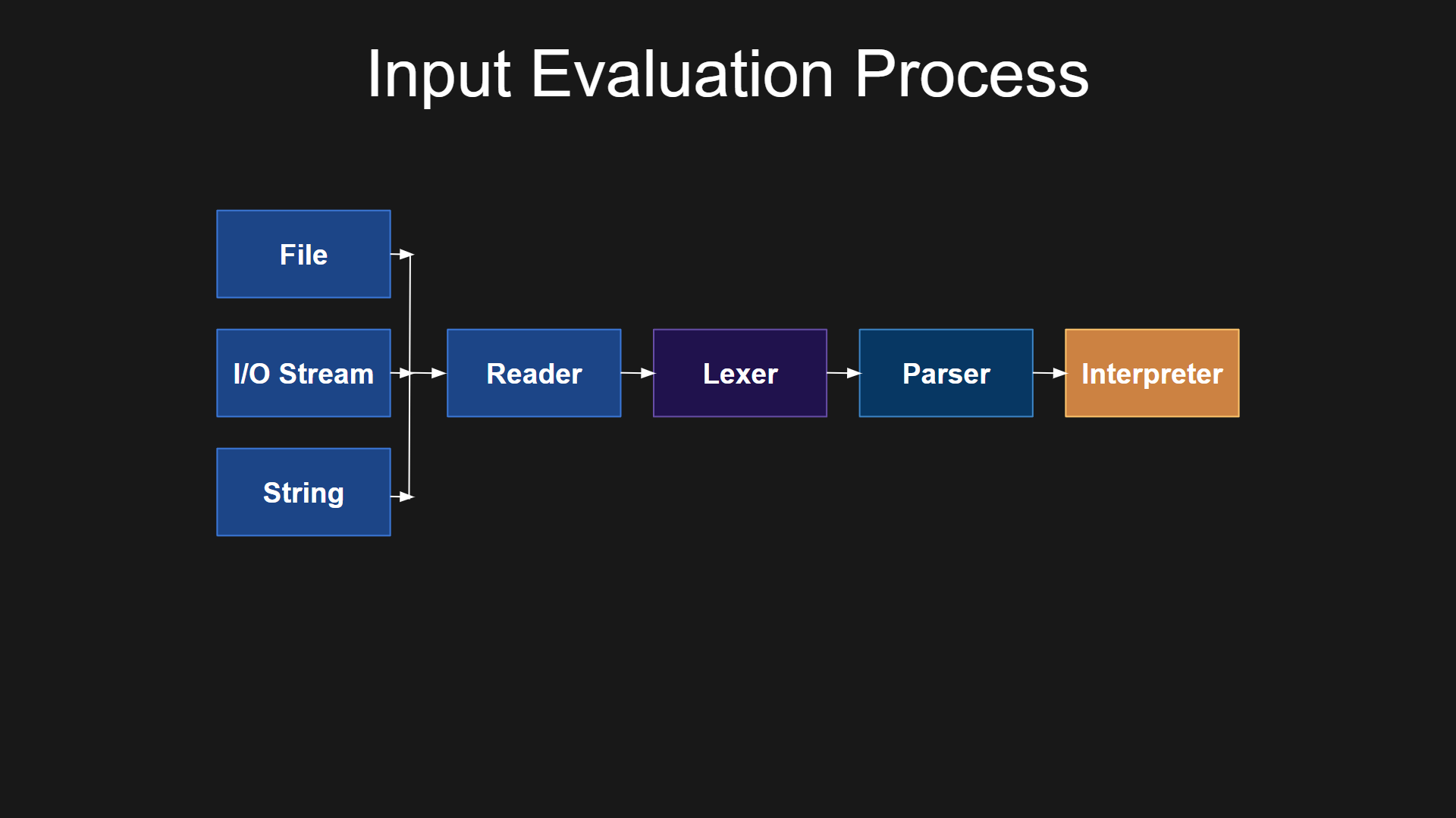
Previous Posts:
Creating TuffScript: Exploring Esoteric Programming Languages and Their Foundations
Mastering Formal Grammars: An Introduction to the Chomsky Hierarchy
Precedence and Associativity in Grammar Rules
Mastering Lexical and Syntax Analysis: An Exploration of Tokenizers and Parsers
Arithmetic Expressions Evaluator: Part 1
Syntax Validator
As you may remember, we defined a parser as a program that checks if the source code follows the grammar rules of a language. For now, let's forget about creating an Abstract Syntax Tree (AST). Let's focus on creating a program that ensures our arithmetic expressions are grammatically correct. As mentioned before, we will create a recursive descent parser that uses mutually recursive functions to process input. Each function corresponds to a non-terminal in the grammar and checks if the input matches that rule by reading tokens one by one. If the sequence of tokens does not match the expected structure, the parser signals an issue. You might have already heard that this approach directly reflects the structure of the grammar. We'll see how it works.
We have the following grammar for arithmetic expressions, which we finished in the last article:
<expression> ::= <term> <expression'>
<expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
<term> ::= <factor> <term'>
<term'> ::= * <factor> <term'> | / <factor> <term'> | ε
<factor> ::= <number> | ( <expression> )
<number> ::= <digit> | <number> <digit>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
We also created a Tokenizer that handles the lexical analysis and raises an error if there are any unexpected characters in the input.
Now, let's look at how our Syntax Validator will work, using the sequence of tokens received from our Lexer.
Let's define the properties our main class should have and the helper functions we can add to make the parsing process more clear and straightforward.
class SyntaxValidator {
constructor(tokens) {
this.tokens = tokens;
this.currentTokenIndex = 0;
}
currentToken() {
return this.tokens[this.currentTokenIndex];
}
nextToken() {
++this.currentTokenIndex;
}
}
Here, the SyntaxValidator class is initialized with an array of tokens. The currentTokenIndex keeps track of which token we are analyzing. The currentToken() function returns the current token, and nextToken() moves to the next one. Of course, it would be good to add some checks to prevent going out of the array bounds. But for now, let's keep things as short and simple as possible. Our simple Syntax Validator will return true or false based on the input.
Let's also create some helper functions to help us check whether the current token matches a specific type or value.
isCurrentTokenKind({ kind }) {
const token = this.currentToken();
return token && token.type.name === kind;
}
isCurrentTokenBinaryOperator({ operator }) {
return (
this.isCurrentTokenKind({ kind: TOKEN_KIND.BinaryOperator }) &&
this.currentToken().value === operator
);
}
To handle error messages, let's create two more functions: one to use when we expect a specific token but receive something else, and another to display a general "unexpected token" message.
require({ expected, message }) {
if (!this.isCurrentTokenKind({ kind: expected })) {
console.error(
message ??
`Expected ${expected}, at position: ${this.currentTokenIndex}`,
);
return false;
}
this.nextToken();
return true;
}
reportUnexpectedToken() {
const token = this.currentToken();
console.error(
`Unexpected token: ${token.type.name} ${token.value}, at position: ${this.currentTokenIndex}`,
);
}
In real-world scenarios, error handling is often more complex and typically involves raising an error instead of just showing an error message. However, the main goal of building our small, simple Syntax Validator is to demonstrate the core principles behind every recursive descent parser algorithm. For our purposes, these basic functions are enough.
Our Syntax Validator needs a main function that will attempt to validate the sequence of tokens we pass to it. In our case, it looks like this:
parse() {
if (this.expression()) {
return this.require({ expected: TOKEN_KIND.EOF });
}
return false;
}
As you can see, it first checks if the token sequence forms a valid expression using the this.expression() method (which we will create next). If the expression is valid, it ensures the input ends with an EOF token. If everything is correct, it returns true; otherwise, it returns false, indicating that either the EOF token wasn't reached or there are other issues in the arithmetic expression.
Now let's create the main expression() method to parse arithmetic expressions and see how it, along with the other methods for non-terminals, reflects the grammar rules.
expression() {
// <expression> ::= <term> <expression'>
if (this.term()) {
return this.expressionPrime();
}
return false;
}
The expression() function corresponds directly to the expression rule in the grammar. It first tries to parse a term (a required part of any expression). If the term is parsed successfully, it moves on to parsing expressionPrime(). If the term was not parsed successfully, it indicates a syntax error, and the function returns false.
The expressionPrime() function will operate as follows:
expressionPrime() {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
this.nextToken();
if (this.term()) {
return this.expressionPrime();
}
return false;
}
// ε case (empty production)
return true;
}
The expressionPrime() function is responsible for handling the continuation of an arithmetic expression with + or -. It first checks if the current token is either a + or -. If it is, the function advances to the next token, calls the term() function to parse the next part of the expression, and then recursively calls expressionPrime() to handle any additional + or - operators. If neither operator is found, the function assumes an empty production (ε) and returns true, indicating the expression has been successfully parsed.
Even without finalizing our Syntax Analyzer, you can already notice that these methods are essentially reflections of our grammar rules. They directly replicate the underlying logic of our grammar.
Moving forward, let's see how the term() method, which corresponds to the non-terminal "term" in our grammar, should work:
term() {
// <term> ::= <factor> <term'>
if (this.factor()) {
return this.termPrime();
}
return false;
}
termPrime() {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
this.nextToken();
if (this.factor()) {
return this.termPrime();
}
return false;
}
// ε case (empty production)
return true;
}
Similar to the methods for handling the "expression" non-terminal, which can contain + or - operators, the "term" non-terminal consists of a "factor" followed by an optional continuation (termPrime()), allowing for * and / operators in our arithmetic expressions.
This structure directly follows the grammar's definition of a "term". Since the term() function is part of the process for evaluating an "expression", it ensures that parts of arithmetic expressions with * or / are evaluated before those with + or -. This matches the expected order of operations in arithmetic.
Now, let's look at how the base of this recursive process works—the factor() method, which handles the "factor" non-terminal in our code:
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
this.nextToken();
return true;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
if (this.expression()) {
return this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
}
return false;
}
this.reportUnexpectedToken();
return false;
}
The factor() function is a crucial part of our parser. It handles both the base case when the current token is a number and the case when we encounter an open parenthesis. An open parenthesis signals the start of a new <expression> non-terminal, triggering a recursive process to evaluate everything inside. This can lead to nested expressions, potentially expanding further, as the parser continues until the entire content within the parentheses is fully processed.
When the function starts, it first checks if the current token is a number. If it is, the base case has been reached, so we "consume" the current token, move forward, and return true.
If the current token is an opening parenthesis, the parser advances to the next token and calls the expression() function to analyze the contents within the parentheses. After processing the expression, we must ensure there is a closing parenthesis. If the closing parenthesis is missing, it indicates a syntax error, so we need to return false and report the issue.
If neither a number nor an opening parenthesis is found when calling factor(), it means there's a syntax error, so the function reports an unexpected token, indicating the input doesn't match the expected format, and returns false.
Now, let's bring everything together in our SyntaxValidator class. Inside the parser folder from the previous article, create a new file named syntaxValidator.js and add the following code:
const { TOKEN_KIND, BINARY_OPERATOR } = require('../lexer/constants');
class SyntaxValidator {
constructor(tokens) {
this.tokens = tokens;
this.currentTokenIndex = 0;
}
currentToken() {
return this.tokens[this.currentTokenIndex];
}
nextToken() {
++this.currentTokenIndex;
}
isCurrentTokenKind({ kind }) {
const token = this.currentToken();
return token && token.type.name === kind;
}
isCurrentTokenBinaryOperator({ operator }) {
return (
this.isCurrentTokenKind({ kind: TOKEN_KIND.BinaryOperator }) &&
this.currentToken().value === operator
);
}
require({ expected, message }) {
if (!this.isCurrentTokenKind({ kind: expected })) {
console.error(
message ??
`Expected ${expected}, at position: ${this.currentTokenIndex}`,
);
return false;
}
this.nextToken();
return true;
}
reportUnexpectedToken() {
const token = this.currentToken();
console.error(
`Unexpected token: ${token.type.name} ${token.value}, at position: ${this.currentTokenIndex}`,
);
}
parse() {
if (this.expression()) {
return this.require({ expected: TOKEN_KIND.EOF });
}
return false;
}
expression() {
// <expression> ::= <term> <expression'>
if (this.term()) {
return this.expressionPrime();
}
return false;
}
expressionPrime() {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
this.nextToken();
if (this.term()) {
return this.expressionPrime();
}
return false;
}
// ε case (empty production)
return true;
}
term() {
// <term> ::= <factor> <term'>
if (this.factor()) {
return this.termPrime();
}
return false;
}
termPrime() {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
this.nextToken();
if (this.factor()) {
return this.termPrime();
}
return false;
}
// ε case (empty production)
return true;
}
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
this.nextToken();
return true;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
if (this.expression()) {
return this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
}
return false;
}
this.reportUnexpectedToken();
return false;
}
}
module.exports = {
SyntaxValidator,
};
Let’s also update our index.js file, which serves as the entry point, to display the validation results.
const readline = require('readline');
const { Lexer } = require('./lexer');
const { SyntaxValidator } = require('./parser/syntaxValidator');
const readlineInterface = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
function waitForUserInput() {
readlineInterface.question('Input expression: ', function (input) {
if (input.toLocaleLowerCase() === 'exit') {
return readlineInterface.close();
}
if (!input.trim()) {
return waitForUserInput();
}
const lexer = new Lexer(input);
const tokens = lexer.tokenize();
const syntaxValidator = new SyntaxValidator(tokens);
const syntaxValidationResult = syntaxValidator.parse();
console.log('Output: ', syntaxValidationResult);
waitForUserInput();
});
}
waitForUserInput();
Now, if we run our program and input something like 2 + 2, we should see the validation results. Additionally, for demonstration purposes, I’ve added console.log statements in the methods that represent non-terminals to show how the call stack is constructed and how the validation process runs.
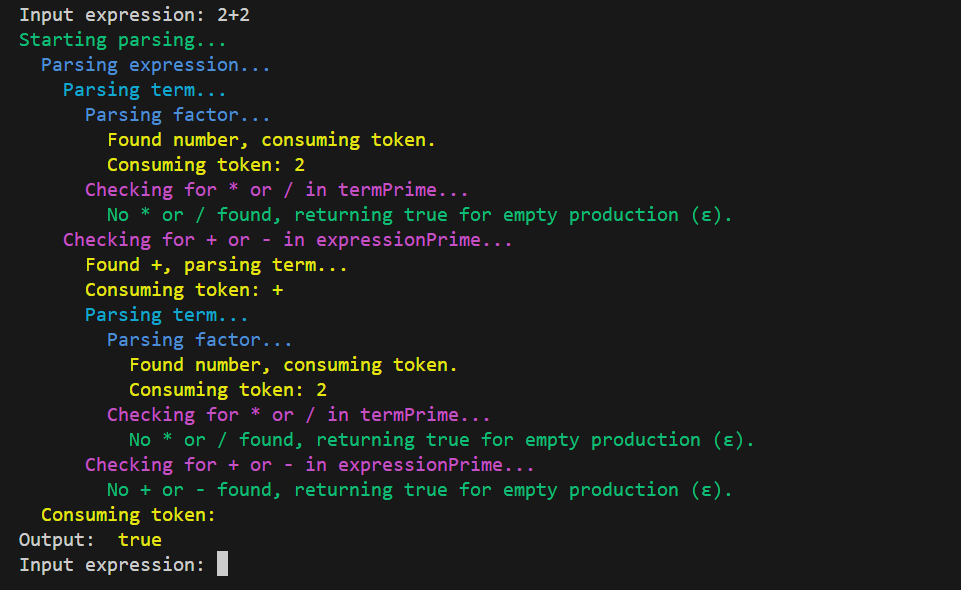
We can also input an invalid expression to see how the Syntax Validator handles it:
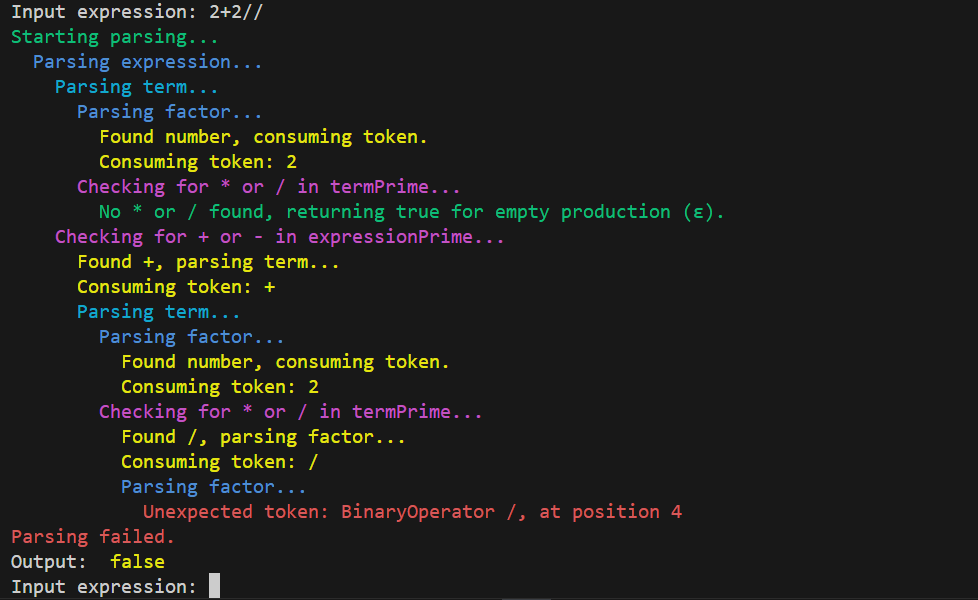
I highly recommend carefully reviewing the order in which the methods are called. Copy and paste the code we’ve written so far, run it yourself using a debugger, and go through each step to see how it works. This is the best way to truly understand how a recursive parser operates.
Building the AST
Now, let’s consider how we can use this process to create an AST.
The main goal is to return AST nodes instead of booleans that merely indicate the validity of the input string's syntax.
Let’s also start throwing errors when we encounter syntax issues, instead of just displaying messages and returning false. We'll need to make a few small adjustments to our helper functions to support error throwing.
require({ expected, message }) {
if (!this.isCurrentTokenKind({ kind: expected })) {
throw new Error(
message ??
`Expected ${expected}, at position: ${this.currentTokenIndex}`,
);
}
this.nextToken();
}
reportUnexpectedToken() {
const token = this.currentToken();
throw new Error(
`Unexpected token: ${token.type.name} ${token.value}, at position: ${this.currentTokenIndex}`,
);
}
Now, let’s review our methods, which correspond to non-terminals, and see what changes need to be made.
Let’s begin with the main parse() method.
Previous implementation:
parse() {
if (this.expression()) {
return this.require({ expected: TOKEN_KIND.EOF });
}
return false;
}
New implementation:
parse() {
const result = this.expression();
this.require({ expected: TOKEN_KIND.EOF });
return result;
}
I believe the changes to this function are straightforward. First, we attempt to parse the main expression by calling the this.expression() method. If everything goes smoothly and no errors are thrown, the result is likely a valid AST. Before returning the result, the only thing we need to check is whether we’ve reached the end of the token list. If we have, everything is fine, and we can return the result of the this.expression() call. However, if the current token is not the end of file (EOF), it means there’s a syntax issue, and the this.require() method will automatically throw an error.
Now, let’s take a look at how the this.expression() function needs to be changed.
Previous implementation:
expression() {
// <expression> ::= <term> <expression'>
if (this.term()) {
return this.expressionPrime();
}
return false;
}
New implementation:
expression() {
// <expression> ::= <term> <expression'>
const term = this.term();
return this.expressionPrime({ term });
}
The key point here is that we first attempt to parse the term, just as we did before, following the grammar. However, since a compound expression may contain operators like - or +, we need to pass the AST node created by the term() method to expressionPrime({ term }). This preserves the context of the previous method, allowing us to create a binary operation node if necessary. And of course, instead of returning booleans, we will return an AST node.
Now, let’s dive into the expressionPrime({ term }) function and explore the differences between the new and previous implementations.
Previous implementation:
expressionPrime() {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
this.nextToken();
if (this.term()) {
return this.expressionPrime();
}
return false;
}
// ε case (empty production)
return true;
}
New implementation:
expressionPrime({ term }) {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.term();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: term,
right: rightNode,
});
return this.expressionPrime({ term: binaryOperationNode });
}
// ε case (empty production)
return term;
}
As you can see, when there are no - or + operators, instead of returning a boolean value indicating an empty production rule, we return the term received as the context value.
However, if we encounter - or + operators, we need to store the operator type and "eat" the current token by calling the .nextToken() method. After that, we proceed to parse the next term as specified by the grammar.
If you recall from the previous article, we discussed fixing operator associativity during the parsing stage. To make the - and + operators left-associative, we use the received term as the left operand when creating a BinaryOperationNode, with the newly parsed term after the operator as the right operand.
Since this process can repeat (for expressions like 2 + 2 + 2 - 2 and so on), we recursively pass the newly created binary expression as the left operand to the next expressionPrime({ term: node }) call. This ensures the process is repeated recursively as needed.
If you understand this recursive part, where the expressionPrime() method calls itself to create binary nodes for consecutive - and + operators, then you're starting to grasp how a recursive descent parser works.
The same logic applies to the term() and termPrime() functions, as the * and / operators are also left-associative and follow a similar AST node construction process. So, let’s briefly review the changes and then move on to the base of the recursion, the factor() method.
The logic for the term() method is as follows.
Previous implementation:
term() {
// <term> ::= <factor> <term'>
if (this.factor()) {
return this.termPrime();
}
return false;
}
New implementation:
term() {
// <term> ::= <factor> <term'>
const factor = this.factor();
return this.termPrime({ factor });
}
Let’s also take a look at the differences between the old and new termPrime() functions.
Previous implementation:
termPrime() {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
this.nextToken();
if (this.factor()) {
return this.termPrime();
}
return false;
}
// ε case (empty production)
return true;
}
New implementation:
termPrime({ factor }) {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.factor();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: factor,
right: rightNode,
});
return this.termPrime({ factor: binaryOperationNode });
}
// ε case (empty production)
return factor;
}
Now, we need to understand how the factor() method works in our new implementation. Once we do that, we’ll be ready to test our parser and see the AST it creates.
Previous implementation:
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
this.nextToken();
return true;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
if (this.expression()) {
return this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
}
return false;
}
this.reportUnexpectedToken();
return false;
}
New implementation:
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
const node = new NumberNode({value: parseFloat(this.currentToken().value)});
this.nextToken();
return node;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
const node = this.expression();
this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
return node;
}
this.reportUnexpectedToken();
}
As you can see, the changes are not as significant as we might have expected. The key difference is that, instead of returning booleans, we now return AST nodes, just like we did for the other methods representing non-terminals.
When we reach the base of the recursion and the token type is a number, we simply create a NumberNode and return it.
If we encounter an open parenthesis, indicating the start of a new expression, we recursively call the this.expression() method, which should return a valid AST. Afterward, we ensure there is a closing parenthesis, and then, instead of returning a boolean, we return the AST node.
Of course, if we reach the base of the recursion and the current token is neither a number nor an opening parenthesis, we throw a syntax error.
After implementing all these changes and creating a file named parserVersion1.js in our parser folder, we get the following result:
const { NumberNode, BinaryOperationNode } = require('./astNode');
const { TOKEN_KIND, BINARY_OPERATOR } = require('../lexer/constants');
class Parser {
constructor(tokens) {
this.tokens = tokens;
this.currentTokenIndex = 0;
}
currentToken() {
return this.tokens[this.currentTokenIndex];
}
nextToken() {
++this.currentTokenIndex;
}
isCurrentTokenKind({ kind }) {
const token = this.currentToken();
return token && token.type.name === kind;
}
isCurrentTokenBinaryOperator({ operator }) {
return (
this.isCurrentTokenKind({ kind: TOKEN_KIND.BinaryOperator }) &&
this.currentToken().value === operator
);
}
require({ expected, message }) {
if (!this.isCurrentTokenKind({ kind: expected })) {
throw new Error(
message ??
`Expected ${expected}, at position: ${this.currentTokenIndex}`,
);
}
this.nextToken();
}
reportUnexpectedToken() {
const token = this.currentToken();
throw new Error(
`Unexpected token: ${token.type.name} ${token.value}, at position: ${this.currentTokenIndex}`,
);
}
parse() {
const result = this.expression();
this.require({ expected: TOKEN_KIND.EOF });
return result;
}
expression() {
// <expression> ::= <term> <expression'>
const term = this.term();
return this.expressionPrime({ term });
}
expressionPrime({ term }) {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.term();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: term,
right: rightNode,
});
return this.expressionPrime({ term: binaryOperationNode });
}
// ε case (empty production)
return term;
}
term() {
// <term> ::= <factor> <term'>
const factor = this.factor();
return this.termPrime({ factor });
}
termPrime({ factor }) {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.factor();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: factor,
right: rightNode,
});
return this.termPrime({ factor: binaryOperationNode });
}
// ε case (empty production)
return factor;
}
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
const node = new NumberNode({value: parseFloat(this.currentToken().value)});
this.nextToken();
return node;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
const node = this.expression();
this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
return node;
}
this.reportUnexpectedToken();
}
}
module.exports = {
Parser,
};
The name "parserVersion1.js" isn't accidental — it's a bit of a teaser. We'll still be making changes to our parser to give it a more classic structure, similar to what you might see in other versions of recursive descent parsers for arithmetic expressions.
For now, let's use it to see the output we get when running our parser.
After updating our main index.js file, here's what we have:
const readline = require('readline');
const { Lexer } = require('./lexer');
const { Parser } = require('./parser/parserVersion1');
const readlineInterface = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
function waitForUserInput() {
readlineInterface.question('Input expression: ', function (input) {
if (input.toLocaleLowerCase() === 'exit') {
return readlineInterface.close();
}
if (!input.trim()) {
return waitForUserInput();
}
const lexer = new Lexer(input);
const tokens = lexer.tokenize();
const parser = new Parser(tokens);
const parserResult = parser.parse();
console.log('Output: ', parserResult);
waitForUserInput();
});
}
waitForUserInput();
Now, for example, running the program with 2+2/2*2-5 as input will produce:
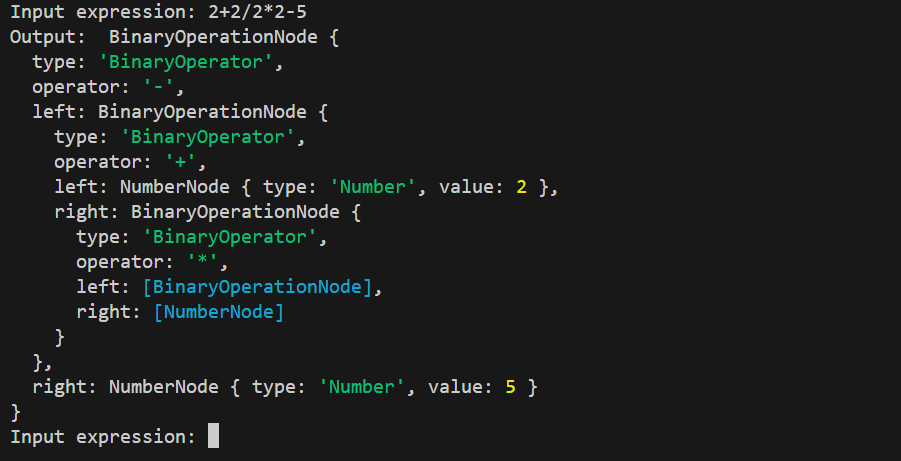
This is a big step! We've finally created an AST based on our grammar, using everything we've learned so far.
Merging Functions for Non-Terminals
Our recursive parser is functioning correctly, and technically, we could stop here and move on to the interpretation stage. However, it's interesting to note that when you search for recursive descent parsers, especially for arithmetic expressions, the methods for handling the "expression" and "term" non-terminals often look a bit different from ours. We've built our parser step by step, starting as a syntax validator and evolving into its current form, to demonstrate the transition from a precise definition of recursive parsers to a more classic implementation, which hides some unnecessary recursive calls.
Now, let's see how we can merge some of our methods for handling non-terminals to give our parser a more traditional structure.
We'll begin by looking at the "expression" non-terminal, which currently contains "expressionPrime", and explore how we can combine the logic of these two functions to handle the + and - operators.
Previous implementation:
expression() {
// <expression> ::= <term> <expression'>
const term = this.term();
return this.expressionPrime({ term });
}
expressionPrime({ term }) {
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
if (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.term();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: term,
right: rightNode,
});
return this.expressionPrime({ term: binaryOperationNode });
}
// ε case (empty production)
return term;
}
New implementation:
expression() {
// <expression> ::= <term> <expression'>
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
let node = this.term();
while (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
const operator = this.currentToken();
this.nextToken();
node = new BinaryOperationNode({
operator: operator.value,
left: node,
right: this.term(),
});
}
return node;
}
You can see that we've merged the logic from the expression() and expressionPrime({term}) methods. While the previous version more accurately reflected our grammatical structure by implementing separate methods for handling the two non-terminals, the new version simplifies things by removing one recursive call. Instead, we use a while loop to collect all the binary nodes produced by consecutive - or + operators.
If you've researched recursive parsers before reading this article, you may have noticed that most of them resemble this new implementation.
Now we can see how we got here, and it's important to remember where we started.
We need to apply the same approach to the term() and termPrime({ factor }) methods.
Previous implementation:
term() {
// <term> ::= <factor> <term'>
const factor = this.factor();
return this.termPrime({ factor });
}
termPrime({ factor }) {
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
if (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
const operator = this.currentToken();
this.nextToken();
const rightNode = this.factor();
const binaryOperationNode = new BinaryOperationNode({
operator: operator.value,
left: factor,
right: rightNode,
});
return this.termPrime({ factor: binaryOperationNode });
}
// ε case (empty production)
return factor;
}
New implementation:
term() {
// <term> ::= <factor> <term'>
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
let node = this.factor();
while (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
const operator = this.currentToken();
this.nextToken();
node = new BinaryOperationNode({
operator: operator.value,
left: node,
right: this.factor(),
});
}
return node;
}
It's almost a copy-paste of the expression() method, but this one is for the "term" non-terminal, of course.
We don't need to change anything else. Let's simply write the final version in the index.js file of our parser folder:
const { NumberNode, BinaryOperationNode } = require('./astNode');
const { TOKEN_KIND, BINARY_OPERATOR } = require('../lexer/constants');
class Parser {
constructor(tokens) {
this.tokens = tokens;
this.currentTokenIndex = 0;
}
currentToken() {
return this.tokens[this.currentTokenIndex];
}
nextToken() {
++this.currentTokenIndex;
}
isCurrentTokenKind({ kind }) {
const token = this.currentToken();
return token && token.type.name === kind;
}
isCurrentTokenBinaryOperator({ operator }) {
return (
this.isCurrentTokenKind({ kind: TOKEN_KIND.BinaryOperator }) &&
this.currentToken().value === operator
);
}
require({ expected, message }) {
if (!this.isCurrentTokenKind({ kind: expected })) {
throw new Error(
message ??
`Expected ${expected}, at position: ${this.currentTokenIndex}`,
);
}
this.nextToken();
}
reportUnexpectedToken() {
const token = this.currentToken();
throw new Error(
`Unexpected token: ${token.type.name} ${token.value}, at position: ${this.currentTokenIndex}`,
);
}
parse() {
const result = this.expression();
this.require({ expected: TOKEN_KIND.EOF });
return result;
}
expression() {
// <expression> ::= <term> <expression'>
// <expression'> ::= + <term> <expression'> | - <term> <expression'> | ε
let node = this.term();
while (
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.PLUS }) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.MINUS })
) {
const operator = this.currentToken();
this.nextToken();
node = new BinaryOperationNode({
operator: operator.value,
left: node,
right: this.term(),
});
}
return node;
}
term() {
// <term> ::= <factor> <term'>
// <term'> ::= * <factor> <term'> | / <factor> <term'> | ε
let node = this.factor();
while (
this.isCurrentTokenBinaryOperator({
operator: BINARY_OPERATOR.MULTIPLY,
}) ||
this.isCurrentTokenBinaryOperator({ operator: BINARY_OPERATOR.DIVIDE })
) {
const operator = this.currentToken();
this.nextToken();
node = new BinaryOperationNode({
operator: operator.value,
left: node,
right: this.factor(),
});
}
return node;
}
factor() {
// <factor> ::= <number> | ( <expression> )
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.Number })) {
const node = new NumberNode({
value: parseFloat(this.currentToken().value),
});
this.nextToken();
return node;
}
if (this.isCurrentTokenKind({ kind: TOKEN_KIND.OpenParen })) {
this.nextToken();
const node = this.expression();
this.require({
expected: TOKEN_KIND.CloseParen,
message: 'Expected closing parenthesis',
});
return node;
}
this.reportUnexpectedToken();
}
}
module.exports = {
Parser,
};
After updating the root index.js file, we get the following:
const readline = require('readline');
const { Lexer } = require('./lexer');
const { Parser } = require('./parser');
const readlineInterface = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
function waitForUserInput() {
readlineInterface.question('Input expression: ', function (input) {
if (input.toLocaleLowerCase() === 'exit') {
return readlineInterface.close();
}
if (!input.trim()) {
return waitForUserInput();
}
const lexer = new Lexer(input);
const tokens = lexer.tokenize();
const parser = new Parser(tokens);
const parserResult = parser.parse();
console.log('Output: ', parserResult);
waitForUserInput();
});
}
waitForUserInput();
If you run the program with the previous input (2+2/2*2-5), you should see the same result as before:

Let’s visualize this process:
I think it's time to finalize our arithmetic expressions evaluator by creating an interpreter that will take the AST and evaluate it.
Interpreter
We're ready to create an interpreter for our arithmetic expressions evaluator, and to be honest, this will be the easiest part for us. Typically, interpreter logic can be much more complex than the code in the parser. However, for our simple interpreter of arithmetic expressions, which will receive a valid AST, we don't need to do much. We'll just use the Visitor Pattern we discussed earlier.
We can even write the entire code for our interpreter all at once. Just create an index.js file in the "interpreter" folder located in the root directory, and add the following code:
const { ASTVisitor } = require('../parser/visitor');
const { BINARY_OPERATOR } = require('../lexer/constants');
class Interpreter extends ASTVisitor {
constructor(root) {
super();
this.root = root;
}
interpret() {
return this.root.accept(this);
}
visitNumberNode(node) {
return node.value;
}
visitBinaryOperationNode(node) {
let left = node.left.accept(this);
let right = node.right.accept(this);
switch (node.operator) {
case BINARY_OPERATOR.PLUS:
return left + right;
case BINARY_OPERATOR.MINUS:
return left - right;
case BINARY_OPERATOR.MULTIPLY:
return left * right;
case BINARY_OPERATOR.DIVIDE:
return left / right;
default:
throw new Error(`Unknown operator: ${node.operator}`);
}
}
}
module.exports = {
Interpreter,
};
And that's it! This is the complete logic of our arithmetic expressions interpreter.
The Interpreter class extends the ASTVisitor class, utilizing the Visitor design pattern to traverse the AST. When an instance of the Interpreter is created, it is initialized with a root node, which represents the top-level node to be interpreted — the starting point of the evaluation.
The interpret() method begins the evaluation process by calling accept on the root node. The accept() method, part of the Visitor pattern, allows the interpreter to visit and evaluate different types of nodes accordingly.
When the interpreter encounters a number node, it simply returns the numerical value using the visitNumberNode() method. This is the most basic form of evaluation, as numbers evaluate to themselves.
The visitBinaryOperationNode() method handles binary operations (e.g., addition, subtraction, multiplication, division) by recursively evaluating the left and right child nodes. Based on the operator (+, -, *, /), it performs the corresponding mathematical operation on the evaluated results of the child nodes.
If the interpreter encounters an unknown operator, it throws an error, indicating that the operation is not supported.
If we visualize this process, it would look like this:

In general, if we visualize the process of evaluating input, the key steps can be illustrated like this:
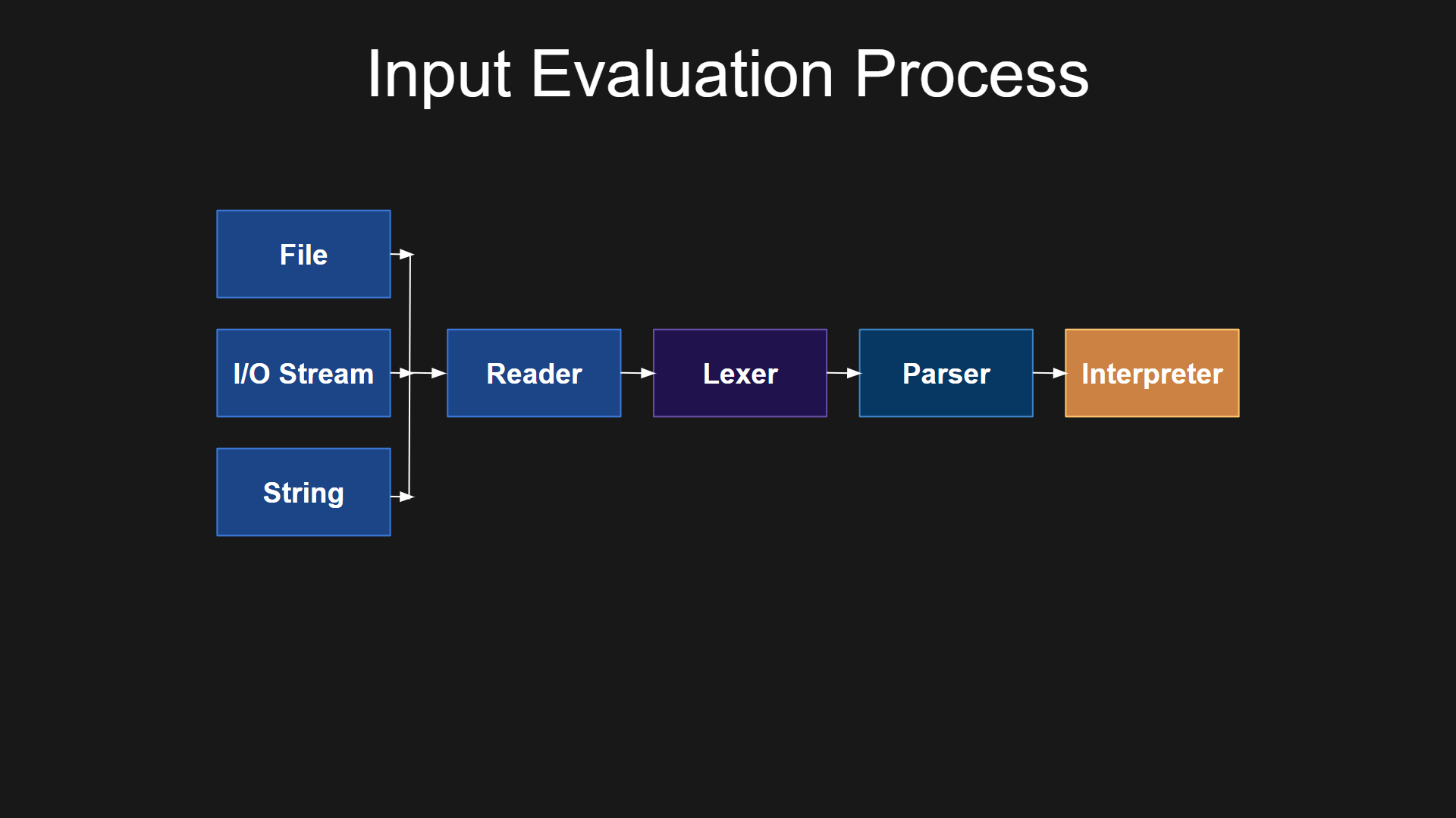
Conclusion
To fully understand the logic of the recursive top-down parser, I highly recommend running the code and walking through each step with a debugger.
We've covered many topics related to grammars, lexical analysis, and various parsing strategies. Now, we've finally created our arithmetic expressions evaluator, which is a big step toward understanding how parsers and interpreters work.
With all these concepts, we're now ready to build more complex programs. For example, a programming language like TuffScript, which we'll be developing.
So, stay tuned for new updates!
Subscribe to my newsletter
Read articles from arman takmazyan directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

arman takmazyan
arman takmazyan
Passionate about building high-performance web applications with React. In my free time, I love diving into the fascinating world of programming language principles and uncovering their intricacies.