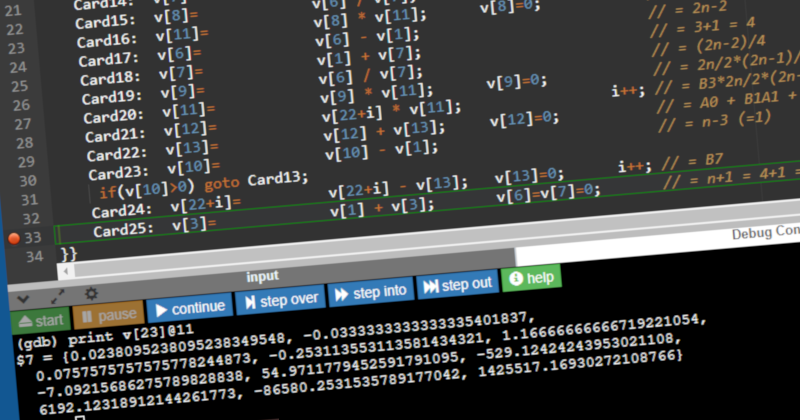
This is the sixth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program

A Recap

In my last post, I ran Ada Lovelace's program and it output the right answer. I ran it on a modern computer by transliterating to C and then using modern tools to build and run. The transliteration was mostly trivial, though the “Here follows a repetition” loop required a bit more thought.

It didn’t work perfectly as-is. There was a typo in Operation 4, likely introduced in publication, and another bug where Operation 24’s output was negated. These were trivially fixed to match the result mentioned in the “Statement of Results” column.

The other change needed was modifying the C for Operation 21 to use auto-increment addressing as discussed in the text of Note G.

In the end, it succeeding in generating B7 correctly as -0.0333333333333333

It Worked, But Not “to an indefinite extent, from the very beginning”

I'm not done, though. In talking about the use of variables in the program, Lovelace makes it clear that the program is expected to continue calculating indefinitely:

It is true that if we consider our computation of B7 as a perfectly isolated calculation, we may conclude B1, B3, B5 to have been arbitrarily placed on the columns; [...] But we are not taking this view. On the contrary, we suppose the engine to be in the course of computing the Numbers to an indefinite extent, from the very beginning;

Implied Outer Loop

The first clue to what we need to do is Operation 25. V3, the variable representing n, is incremented. This would be useless if the program finished at this point. And indeed, Lovelace makes clear her intent after the loop from Operation 13 to 23 completes:

In this state the only remaining processes are, first, to transfer the value which is on V13 to V24; and secondly, to reduce V6, V7, V13 to zero, and to add one to V3, in order that the engine may be ready to commence computing B9. Operations 24 and 25 accomplish these purposes. It may be thought anomalous that Operation 25 is represented as leaving the upper index of V3 still=unity; but it must be remembered that these indices always begin anew for a separate calculation, and that Operation 25 places upon V3 the first value for the new calculation.

Note 20. It is interesting to observe, that so complicated a case as this calculation of the Bernoullian Numbers nevertheless presents a remarkable simplicity in one respect; viz. that during the processes for the computation of millions of these Numbers, no other arbitrary modification would be requisite in the arrangements, excepting the above simple and uniform provision for causing one of the data periodically to receive the finite increment unity.

In Note E, she gives a more general discussion of cycles, including indefinite ones that might now be called infinite loops:

Both for brevity and for distinctness, a recurring group is called a cycle. A cycle of operations, then, must be understood to signify any set of operations which is repeated more than once. It is equally a cycle, whether it be repeated twice only, or an indefinite number of times; for it is the fact of a repetition occurring at all that constitutes it such.

This intent of an indefinite cycle from Operation 1 to 25 would be a simple matter, either causing the cards to automatically back up to the beginning, or possibly physically arranging the cards in a literal loop. As the engine calculated number after number, the operator could watch them appear physically until they choose to halt the engine:

the general form of the whole mass of machinery is that of a quadrangular prism (more or less approaching to the cube); the results always appearing on that perpendicular face of the engine which contains the columns of discs, opposite to which face a spectator may place himself.

Representing this outer, infinite loop in the C transliteration can be done simply by adding boilerplate ‘while(1){ ... }' surrounding operations 1-25.

More Auto-Increment Addressing

In addition to the indefinite cycle, one more piece remains. We need to use auto-increment addressing in Operation 24 the same as we did for Operation 21:

The only exception to a perfect identity in all the processes and columns used, for every repetition of Operations (13…23), is, that Operation 21 always requires one of its factors from a new column, and Operation 24 always puts its result on a new column. But as these variations follow the same law at each repetition (Operation 21 always requiring its factor from a column one in advance of that which it used the previous time, and Operation 24 always putting its result on the column one in advance of that which received the previous result), they are easily provided for in arranging the recurring group (or cycle) of Variable-cards.

As we did before for Operation 21:

Card24: v[24]= v[24] - v[13]; v[13]=0;

Becomes:

Card24: v[22+i]= v[22+i] - v[13]; v[13]=0; i++;

That's it. This is a good point to try another run…

Updated C Code

Here is the updated C transliteration.

int main() { long double v[100] = { 0 };
         v[1]=  1;  // [1]
         v[2]=  2;  // [2]
         v[3]=  3;  // [n]
         v[21] = 1.0/6.0;   // [B1]
         v[22] = -1.0/30.0; // [B3]
while(1){ int i=0;
    Card1:   v[4]=v[5]=v[6]=   v[2] * v[3];                          // = 2n
    Card2:   v[4]=             v[4] - v[1];                          // = 2n-1
    Card3:   v[5]=             v[5] + v[1];                          // = 2n+1
    Card4:   v[11]=            v[4] / v[5];       v[5]=v[4]=0;       // = (2n-1)/(2n+1)
    Card5:   v[11]=            v[11] / v[2];                         // = 1/2*(2n-1)/(2n+1)
    Card6:   v[13]=            v[13] - v[11];     v[11]=0;           // = -1/2*(2n-1)/(2n+1) = A0
    Card7:   v[10]=            v[3] - v[1];                          // = n-1 (=3)
    Card8:   v[7]=             v[2] + v[7];                          // = 2+0 = 2
    Card9:   v[11]=            v[6] / v[7];                          // = 2n/2 = A1
    Card10:  v[12]=            v[21] * v[11];                        // = B1*2n/2 = B1A1
    Card11:  v[13]=            v[12] + v[13];     v[12]=0;           // = -1/2*(2n-1)/(2n+1)+B1*2n/2
    Card12:  v[10]=            v[10] - v[1];                         // = n-2 (=2)
    Card13:  v[6]=             v[6] - v[1];                          // = 2n-1
    Card14:  v[7]=             v[1] + v[7];                          // = 2+1 = 3
    Card15:  v[8]=             v[6] / v[7];                          // = (2n-1)/3
    Card16:  v[11]=            v[8] * v[11];      v[8]=0;            // = 2n/2*(2n-1)/3
    Card17:  v[6]=             v[6] - v[1];                          // = 2n-2
    Card18:  v[7]=             v[1] + v[7];                          // = 3+1 = 4
    Card19:  v[9]=             v[6] / v[7];                          // = (2n-2)/4
    Card20:  v[11]=            v[9] * v[11];      v[9]=0;            // = 2n/2*(2n-1)/3*(2n-2)/4 = A3
    Card21:  v[12]=            v[22+i] * v[11];                 i++; // = B3*2n/2*(2n-1)/3*(2n-2)/3 = B3A3
    Card22:  v[13]=            v[12] + v[13];     v[12]=0;           // = A0 + B1A1 + B3A3
    Card23:  v[10]=            v[10] - v[1];                         // = n-3 (=1)
     if(v[10]>0) goto Card13;
    Card24:  v[22+i]=          v[22+i] - v[13];   v[13]=0;      i++; // = B7
    Card25:  v[3]=             v[1] + v[3];       v[6]=v[7]=0;       // = n+1 = 4+1 = 5; by a Variable-card. by a Variable card.
}}

Does it work, though? I'll try it out below, but remember, you can run this yourself by copy/pasting into onlinegdb, putting a breakpoint at Card25, and watching as each Bernoulli number gets computed.

Changes Required to Get This Far

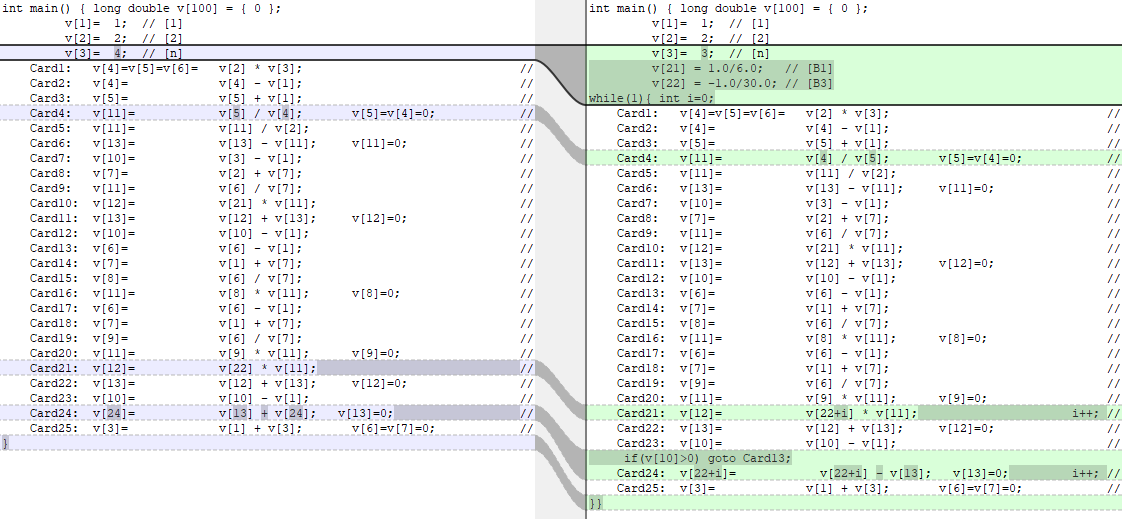
To be clear, in addition to improving the transliteration with a while(1) for the implied outer loop and also handling the inner loop, the set of changes from the original table required to get this far are:

Card4: Fixed a typo error, transposing v[5] and v[4] to match the comment
Card21: Modified for auto-increment addressing by adding "+i" to v[22] and "i++;" at the end.
Card24: Fixed a bug by subtracting v[13] from v[24] instead of adding
Card24: Modified to support auto-increment addressing, similar to Card21

For comparison, here is a diff from the initial naive transliteration without corrections and without support for loops or auto-increment addressing. You can see that it didn't change much:

Running “to an indefinite extent”

Let's see what happens when we run this. Changing the input n to 3 should allow “computing the Numbers to an indefinite extent” from B5 (n = 3) with B1 and B3 being given:

B5 = 0.0238095238095238
B7 = -0.0333333333333335
B9 = 0.0757575757575778
B11 = -0.2531135531135814
B13 = 1.1666666666671922
B15 = -7.0921568627578983
B17 = 54.9711779452591791
B19 = -529.1242424395302111
B21 = 6192.1231891214426177
B23 = -86580.2531535789177042
B25 = 1425517.1693027210876608

Hey! It works!

Revisit Lovelace's Goals

One might think this is a good point to stop, “but we are not taking this view.” It’s perhaps a minor point as B1 and B3 are of course well known and easily computed by hand. A careful read of the table itself as well as Note G makes it clear her intent for the program is not just “to an indefinite extent” but also “from the very beginning.”

Remember her goals:

~~"Compute the [Bernoulli] Numbers"~~
~~"to an indefinite extent"~~~~: iterating to calculate B~~_n~~, B~~_n+1~~, etc. until you choose to halt the machine.~~
"from the very beginning": starting with B₁.
"without having been worked out by human head & hands first": to at least B₆₃.

Starting to Think About Precision

Looking at the list of calculated Bernoulli numbers above, you might have noticed an issue with precision. This is important if we hope to satisfy the 4th goal of calculating up to B₆₃.

The exact fraction for B₇ is -1/30 which is an infinitely repeating decimal, -0.0333... To compare, we calculated it to be B7 = -0.0333333333333335, with 14 correct 3s before the digits become garbage. Not too bad. B₂₅ is 8553103/6 which should similarly end in an infinitely repeating decimal, .16666... For that we calculated B25 = 1425517.1693027210876608, with everything after .16 being garbage. This time only 9 correct digits. Still not too bad, but the trend is worrying.

This reduced precision is largely a consequence of the limitations of built-in C floating point math vs the 50 digit fixed point Babbage proposed for the Analytical Engine. I chose “long double” to get beyond the limitations of the usual 32 bit float and 64 bit double, but it only gets to 80-128 bits depending on platform. This helps get farther along, but eventually compounding error takes over. I will talk more about this later.

Next… “from the very beginning”

But first, let’s work with Lovelace to get this code working “from the very beginning” as intended. Simply changing n to 1 gives garbage results, so there must be something else going on in the code.

In my next blog post, I'll improve my transliteration a bit to get her program computing to an indefinite extent, "from the very beginning."

Part 6: Computing the Bernoulli Numbers to an Indefinite Extent