As I mentioned in my first article of the series about utile.space, I was interesting to do some math.

Ok so, how to compute Pi?

We are in 2024, so the first thing I did is to ask our favorites LLMs to help me with the code.

I tried ChatGPT, Claude, and some others… They all provided me an algorithm… that was not working. And even trying to debug the algorithms with them by reporting errors and such. It was a dead end…

Then I went on Google, I didn’t find anything precisely in Go. So I think we can assume the LLMs were trained on the same data that is not containing a solution for that. Hence they were hallucinating an algorithm mixed on others solution and Go code they learnt.

No LLMs then! Let’s use Human Intelligence…

After reading the wikipedia page of Pi, one of the algorithm mentioned to compute Pi is called Chudnovsky Algorithm.

I am not going into the explanation of the algorithm here, so if you want more details I invite you to check out the wikipedia page about it:

https://en.wikipedia.org/wiki/Chudnovsky_algorithm

The good thing here is that the page provides a Python code to compute it! So now I just need to convert that code to Go!

Converting Python code to Go code

To be honest, I tried again LLMs at that stage to see if they could help…

They were of no help again… except one thing. Thanks to ChatGPT I learnt that the sort of equivalent of the decimal module of Python in Go is math/big.

From now I took the simplest approach to reach my goal: I copy pasted the Python code and converted by hand to Go line by line.

About 20 lines of Python code and mostly math calculation so it’s not that long and complex.

We have a chudnovsky function that takes one argument n which will stop the convergence to Pi. Again this is the formula from Chudnovsky below.

$$\pi =\lim _{n\to \infty }{\frac {426880{\sqrt {10005}}\cdot Q(1,n)}{13591409Q(1,n)+R(1,n)}}$$

Inside the chudnovsky function we then call the recursive function binarySplit.

Challenges of the conversion

The first major difference with Python I encountered has been that Golang does not provide operator overloading. So while in Python is pretty clean using * and / it was not possible with Go and the package math/big.

For instance * has to be replaced by a call to .Mul(x, y) and + by .Add(x, y).

Two others operators in Python gave me a bit of trouble.

Cube

In Python the line is:

Qab = 10939058860032000 * a**3

Looking at the math/big https://pkg.go.dev/math/big#Float I didn’t see any Power function. So I ended writing this simple version of a Cube function for this type:

func cube(v *big.Float) *big.Float {
    result := newBigFloat(1)
    result.Mul(result, v)
    result.Mul(result, v)
    result.Mul(result, v)
    return result
}

If it would have not been a power of 3, I would have probably written a loop. But here I believe this is clear and simple enough. Most important it does the job!

Floor division

In Python the line is:

m = (a + b) // 2

I didn’t know about this operator, and it exists in some others languages. You can find the details here:

But in two words, as its name says, it divides a by b and then floor the result. So in an other word, it’s a Euclidean division.

The good thing here is that as long as my numerator and denominator are integer in Go, the classic / operator is a Euclidean division in Go.

So the conversion simply became:

m := (a + b) / 2

After that, I noticed something was off

For the moment, I disregarded the Python line:

decimal.getcontext().prec = 100 # number of digits of decimal precision

This is a convenient way in Python to change the precision of the big float you are manipulating.
And after reading the big.Float from Go, I noticed that by default they only 53 digits of precision:

NewFloat allocates and returns a new Float set to x, with precision 53 and rounding mode ToNearestEven.

So while I am trying to compute a result of at least 10K decimals, using something with only 53 digits is pretty pointless…

Another annoying thing is there is no one-liner like Python. So I came up with a factory to create my big.Float with the right precision set in advance.

func newBigFloat(v float64) *big.Float {
    return big.NewFloat(v).SetPrec(floatPrecision)
}

All the pieces of the puzzle were now more or less complete now!

And then Pi!

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396665573092547110557853763466820653109896526918620564769312570586356620185581007293606598764861179104533488503461136576867532494416680396265797877185560845529654126654085306143444318586769751456614068007002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830634328587856983052358089330657574067954571637752542021149557615814002501262285941302164715509792592309907965473761255176567513575178296664547791745011299614890304639947132962107340437518957359614589019389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571853061422881375850430633217518297986622371721591607716692547487389866549494501146540628433663937900397692656721463853067360965712091807638327166416274888800786925602902284721040317211860820419000422966171196377921337575114959501566049631862947265473642523081770367515906735023507283540567040386743513622224771589150495309844489333096340878076932599397805419341447377441842631298608099888687413260472156951623965864573021631598193195167353812974167729478672422924654366800980676928238280689964004824354037014163149658979409243237896907069779422362508221688957383798623001593776471651228935786015881617557829735233446042815126272037343146531977774160319906655418763979293344195215413418994854447345673831624993419131814809277771038638773431772075456545322077709212019051660962804909263601975988281613323166636528619326686336062735676303544776280350450777235547105859548702790814356240145171806246436267945612753181340783303362542327839449753824372058353114771199260638133467768796959703098339130771098704085913374641442822772634659470474587847787201927715280731767907707157213444730605700733492436931138350493163128404251219256517980694113528013147013047816437885185290928545201165839341965621349143415956258658655705526904965209858033850722426482939728584783163057777560688876446248246857926039535277348030480290058760758251047470916439613626760449256274204208320856611906254543372131535958450687724602901618766795240616342522577195429162991930645537799140373404328752628889639958794757291746426357455254079091451357111369410911939325191076020825202618798531887705842972591677813149699009019211697173727847684726860849003377024242916513005005168323364350389517029893922334517220138128069650117844087451960121228599371623130171144484640903890644954440061986907548516026327505298349187407866808818338510228334508504860825039302133219715518430635455007668282949304137765527939751754613953984683393638304746119966538581538420568533862186725233402830871123282789212507712629463229563989898935821167456270102183564622013496715188190973038119800497340723961036854066431939509790190699639552453005450580685501956730229219139339185680344903982059551002263535361920419947455385938102343955449597783779023742161727111723643435439478221818528624085140066604433258885698670543154706965747458550332323342107301545940516553790686627333799585115625784322988273723198987571415957811196358330059408730681216028764962867446047746491599505497374256269010490377819868359381465741268049256487985561453723478673303904688383436346553794986419270563872931748723320837601123029911367938627089438799362016295154133714248928307220126901475466847653576164773794675200490757155527819653621323926406160136358155907422020203187277605277219005561484255518792530343513984425322341576233610642506390497500865627109535919465897514131034822769306247435363256916078154781811528436679570611086153315044521274739245449454236828860613408414863776700961207151249140430272538607648236341433462351897576645216413767969031495019108575984423919862916421939949072362346468441173940326591840443780513338945257423995082965912285085558215725031071257012668302402929525220118726767562204154205161841634847565169998116141010029960783869092916030288400269104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157959847035622262934860034158722980534989650226291748788202734209222245339856264766914905562842503912757710284027998066365825488926488025456610172967026640765590429099456815065265305371829412703369313785178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291616152881384379099042317473363948045759314931405297634757481193567091101377517210080315590248530906692037671922033229094334676851422144773793937517034436619910403375111735471918550464490263655128162288244625759163330391072253837421821408835086573917715096828874782656995995744906617583441375223970968340800535598491754173818839994469748676265516582765848358845314277568790029095170283529716344562129640435231176006651012412006597558512761785838292041974844236080071930457618932349229279650198751872127267507981255470958904556357921221033346697499235630254947802490114195212382815309114079073860251522742995818072471625916685451333123948049470791191532673430282441860414263639548000448002670496248201792896476697583183271314251702969234889627668440323260927524960357996469256504936818360900323809293459588970695365349406034021665443755890045632882250545255640564482465151875471196218443965825337543885690941130315095261793780029741207665147939425902989695946995565761218656196733786236256125216320862869222103274889218654364802296780705765615144632046927906821207388377814233562823608963208068222468012248261177185896381409183903673672220888321513755600372798394004152970028783076670944474560134556417254370906979396122571429894671543578468788614445812314593571984922528471605049221242470141214780573455105008019086996033027634787081081754501193071412233908663938339529425786905076431006383519834389341596131854347546495569781038293097164651438407007073604112373599843452251610507027056235266012764848308407611830130527932054274628654036036745328651057065874882256981579367897669742205750596834408697350201410206723585020072452256326513410559240190274216248439140359989535394590944070469120914093870012645600162374288021092764579310657922955249887275846101264836999892256959688159205600101655256375679

Here is Pi up to 10K decimals, that you can get here too: https://utile.space/math

It’s computed dynamically each time. 10K is the reasonable of digits that my server can compute in a reasonable time.

For the fun, I computed 1M decimals too

As just I said, 10K is somehow the limit of my server, but I wanted to go bigger.

I chose to run the computation locally on my computer, with enough precision and let the thing run for 10-15 minutes. Then saved the result in a file.

Thanks to it, you can also access of the first 1M on utile.space by clicking on Lazy load π 1M first decimals.

Technically via a pagination system, you will browse that file I computed on my computer to read the 1M in your browser page by page. IIRC 10K decimals per page.

I didn’t realize before but 1M digits it’s very long…

Hey wait! What about Tau?

Yeah, right! If you don’t know about Tau I invite you to read the Tau manifesto first!

Here: https://utile.space/pdf/tau-manifesto.pdf

In shorts, the main idea is that we often need 2*Pi , not Pi itself. So instead let’s use Tau which is equal to 2*Pi

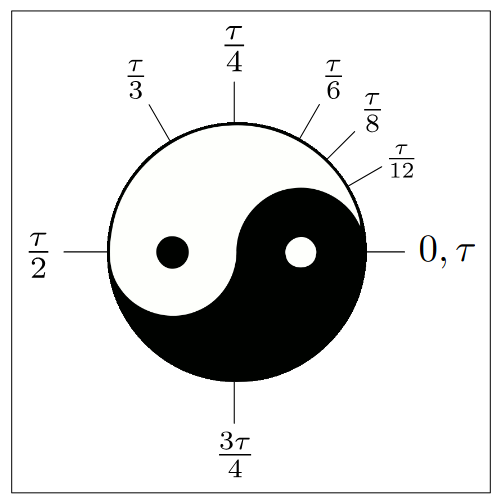
One Tau radians angle is a full circle. Half of Tau of Half a circle.

A bit more logical, isn’t it?

And for the code for it I used the most simple and readable one:

func ChudnovskyTau(n int) *big.Float {
    pi := Chudnovsky(n)
    pi.Mul(pi, newBigFloat(2.0))

    return pi
}

Conclusion, what’s next?

What I retained personally from the experience:

• It demonstrates again that (current) LLMs are a mirror of the current knowledge available on internet

  • I haven’t tried the latest LLMs designed towards reflection and construction of a train of thoughts. I might have some surprise with it.

• I got to know the math/big package in Go.

• I also implemented a websocket server for the purpose of serving the 1M digits of Pi in lazy loading fashion. That websocket that I am going to experience more and more with to create interactive experience.

What’s next? Well the Chudnovsky algorithm I have is single-threaded. From my understanding there are possibilities of parallelizing some of the computation, likely here:

Pam, Qam, Ram := binarySplit(a, m) // on one thread
Pmb, Qmb, Rmb := binarySplit(m, b) // on another

So I might come back to that later. I might also try to compute more digits. To server 10M, 100M, 1B digits of Pi. But not sure yet. Because it represents challenges in terms of size 1B represents 1G and computation time.