Mastering Bit Manipulation: A Step-by-Step Guide
 Sujan Haldar
Sujan Haldar
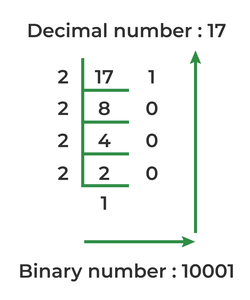
Decimal to Binary conversion
Convert decimal number to binary by divide it using 2 and take reminder in reverse order.
public class Solution{
public String decimalToBinary(int num){
StringBuilder ans = new StringBuilder();
while(num !=0){
if(num%2 == 0) ans.append('0');
else ans.append('1');
num = num/2;
}
return ans.reverse().toString();
}
}
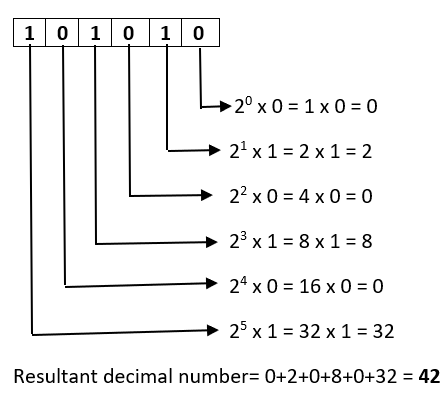
Binary to Decimal conversion
Conver binary number to decimal by multiply 2^(n-1) from right to left.
public class Solution{
public int binaryToDecimal(String binary){
int ans = 0;
int power = 1;
for(int i = binary.length()-1;i>=0;i--){
ans = ans + (power * (binary.charAt(i)-'0'));
power = power*2;
}
return ans;
}
}
How computer store decimal number
Computer store integer number as 32 bit binary number .
For example : 13 → 1101 → 0000……0001101
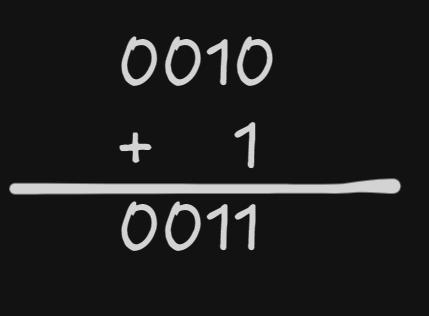
1’s & 2’s Complement
1’s complement : Decimal → Binary → Flip all bit
For example : 13 → 1101 →0010
2’s complement : 1’s complement + 1
For example : 0010+1 →0011
How computer store negetive number
Computer store negetive number as 2’s complement
For an integer 31st bit is for sign. 0 → positive, 1 → Negetive
Step 1 : Convert binary value of positive number
Step 2 : Find out 2’s complement
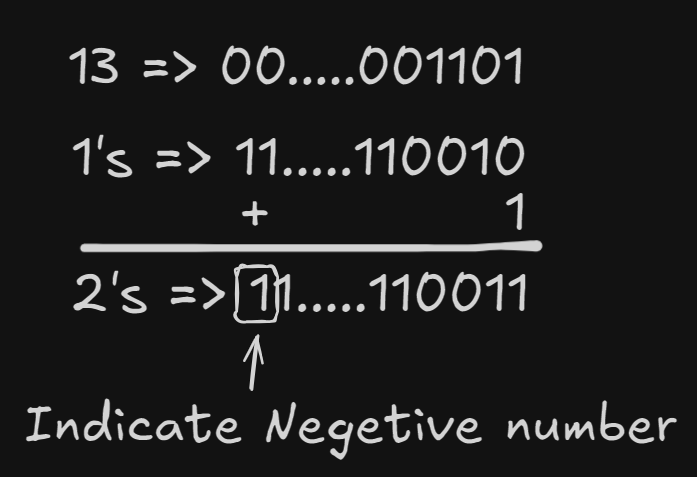
And,Or,XOR,Shift,Not
And : 1 &1 = 1; 1&0 = 0
Or : 1 |1 = 1; 1|0 = 1
XOR : 1 ^ 1= 0; 0^0=0; 1^0 = 1 (Odd number of one or zero : 1; Even number or one or zero : 0)
Right Shift : » (Shift from left to right) → num » k = num / 2^k
Example : 00..001101 » 1 = 00..000110
Left Shift : « (Shift from right to left) → num « k = num* 2^k
Example : 00..001101 » 1 = 00..011010
Not Operator(~) :
Step 1 : Flip all the bit
Step 2 : Check the result of step 1 . If it is negetive ,find out 2’s complement .
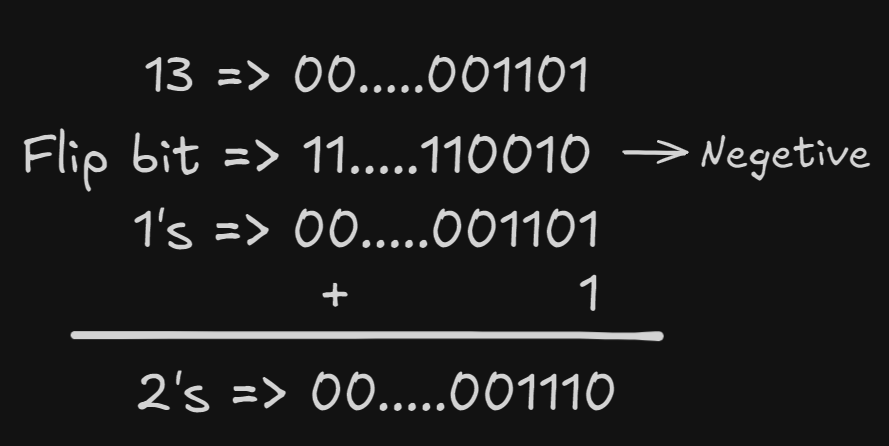
So ~13 = -14
Why -14 : Actually the ~ operator only flip the bit. We flip all bit so sign bit also flip . For positive number after fliping all bit we get negetive number and computer store it as 2’s complement so we don't find out the value of negetive number. That’s why we use 2’s complement to find out original negetive value.
Swap two number using bitwise operator
Let assume two numbers are a & b.
a = a ^ b;
b = a^b = (a^b)^b = a ; (Here a = a ^ b)
a = a^b = (a^b)^a = b ; (Here a = a^b and b = a)
public class SwapNumber {
public static void main(String[] args) {
int a = 5;
int b = 9;
a = a^b;
b = a^b;
a = a^b;
System.out.println(a); // 9
System.out.println(b); // 5
}
}
Check odd or even number
The LSB of odd number is always 1 and even is always 0. So even number always produce zero if we perform num & 1 .
7 = 111 8 = 1000
111 1000
& 001 & 0001
------- -----------
001 0000
public class CheckEvenOrOdd {
public static void evenOrOdd(int num){
int res = num & 1;
if(res == 0){
System.out.println("Even Number");
}else {
System.out.println("Odd Number");
}
}
}
Check the i th bit is set or not
Approach 1 : Using left shift & and operator
Step 1 : Perform left shift of 1 by i. Let i = 2 that menas 1 « 2 = 00…00100 , so only i’th bit is set to 1 and all other bits are 0.
Step 2 : Perform and operation with the input number . If i’th bit of input number is set then we get a value grater than 0 other wise we get 0.
num = 13 = 00..001101
i = 2
i << 2 = 00..00100
00..001101
& 00..000100
---------------
00..000100
public class IthBitSetOrNot {
public boolean CheckIthBitSetOrNot(int num,int i){
int k = 1 << i;
int res = num & k;
return res != 0;
}
}
Approach 2 : Using right shift & and operator
Step 1 : Perform right shift of input number by i. So the i’th bit of input number will be 0’th bit .
Step 2 : Perform and operation with 1. If 0’th bit of right shifted input number is 1 then it produce a resukt grater than 0 otherwise give 0.
num = 13 = 00..001101
i = 2
13 >> 2 = 00..000011
00..000011
& 00..000001
---------------
00..000001
public class IthBitSetOrNot {
public boolean CheckIthBitSetOrNot(int num,int i){
int k = num >> i;
int res = k & 1;
return res != 0;
}
}
Set i’th bit
Perorm left shift of 1 by i . Then perform or operation with input number.
num = 9 = 00..001001
i = 2
1 << 2 = 00..00100
00..001001
| 00..000100
---------------
00..001101
public class SetIthBit {
public int setIthBit(int num,int i){
int k = 1 << i;
return num | k;
}
}
Remove i’th bit
Step 1 : Perform left shift of 1 by i . So the i’th bit is now 1 and all other bit is 0.
Step 2 : Perform not operation with left shifted 1 . So i’th bit is now 0 and all other bits are 1.
Step 2 : Perform and operation with input number.
num = 13 = 00..001101
i = 2
1 << 2 = 00..00100
~(1 << 2) = 11..11011
00..001101
& 11..111011
---------------
00..001001
public class RemoveIthBit {
public int removeIthBit(int num,int i){
int k = ~(1 << i);
return num & k;
}
}
Toggle the i’th bit (0→1 or 1→0)
Step 1 : Perform left shift of 1 by i . So the i’th bit is now 1 and all other bit is 0.
Step 2 : Perform xor operation with input number.
num = 13 = 00..001101
i = 2
1 << 2 = 00..00100
00..001101
^ 00..000100
---------------
00..001001
public class ToggleIthBit {
public static int toggleIthBit(int num,int i){
int k = 1 << i;
return num ^ k;
}
}
Remove the last set bit (Right most bit)
Some observation : For num-1 right most set bit of a num turn to 0 and all other right most unset bit turn to 1.
16 = 10000 40 = 101000 84 = 1010100
15 = 01111 39 = 100111 80 = 1010011
For removing last set bit perform num & (num-1) because both has the same bit before last set bit.
public class RemoveRightMostBit{
public static int removeRightMostBit(int num){
return num & (num-1);
}
}
Check the number is power of 2
The number will be power of 2 if it has only one set bit.
public class CheckPowerOf2{
public static boolean checkPowerOf2(int num){
return (num & (num-1)) == 0;
}
}
Count the number of set bit
num & (num-1) remove right most set bit. So we get number of set bit if we perform num & (num-1) until the num will be 0.
public class CountNumberOfSetBit{
public static int checkCount(int num){
int count = 0;
while(num != 0){
num = num & (num-1);
count++;
}
return count;
}
}
Subscribe to my newsletter
Read articles from Sujan Haldar directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Sujan Haldar
Sujan Haldar
Passionate Computer Science graduate with a strong foundation in software development, eager to contribute to innovative projects and make an impact in the tech industry. Proficient in JAVA , JavaScript with hands-on experience in Node JS.