Stack Gymnastics - Part I

This post is the first of a small series on the topic of stack juggling -- that sometimes mind-boggling art of getting your operands to their operators when coding a stack language (like Forth), or, using the more general and modern term, a concatenative language.

If you are unfamiliar with concatenative programming languages, or if you would like a good overview of the stack juggling difficulty, I would recommend reading, Why Concatenative Language Matters, by Jon Purdy.

Let’s start with a very simple formula written in typical algebraic form.

f(x, y) = (x * y) - (x + y)

How long did it take you to grasp this tiny bit of "code"? Sure, you might not know how this function behaves given various inputs†, but what it does is rather obvious. And, I am fairly certain, you were able to ascertain that in mere seconds.

This code is also rather easy to state in plain English.

The product of two values less their sum.

Now, let's translate that into Forth. But, for the moment, let’s make things easy on ourselves by avoiding stack manipulations using GForth-style local variables.

: f { x y }  x y * x y + - ;

With even the most basic knowledge of concatenative programming, this RPN formulation is easy to understand, certainly no more difficult than our previous algebraic syntax. And hey, look, no more parenthesis!

However, our “easy” way poses a problem. By using local variables, our ability to factor our code is considerably hindered.

At the heart of the issue is a limitation: We can't just arbitrarily extract a portion of the code, give it a name, and expect everything to swim. For example, let's extract the code after * and call it g.

: g  x y + - ;
: f { x y }  x y * g ;

We copied the piece of code verbatim and substituted the new word name, but even so, the system barfs on it 🤮 — complaining it has no idea what x or y are within the scope of g.

: g x y + - ;              
:1: Undefined word
: g >>>x<<< y + - ;

Okay, so we need to define the local variables for g too.

: g { x y } x y + - ;
: f { x y } x y * g ;

Let’s give that a whirl.

1 2 f                                            
:4: Stack underflow
1 2 >>>f<<<
Backtrace:
$73D093857588 >l 
$73D093857618 g

Uh oh. Now we really have to put our thinking cap on! What’s missing? Hmm… Oh right. We need to put the values stored in the local variables back on the stack in order to pass them along to g.

: g { x y } x y + - ;
: f { x y } x y * x y g ;

All good, and honestly, the fix was fairly obvious. Yet this factoring still required extra effort on our part in to ensure variables are passed correctly. In more complex cases it might not be so obvious.

And if you ask me, the code got way more verbugly (verbose, thus ugly, and possibly buggy).

Sure enough, there is a subtle “code smell” here that’s not so obvious at first. It doesn't break anything (thanks to the stack) but it makes the code somewhat obtuse. Can you see what it is?

In contrast, lets rewrite our code in traditional Forth, without local variables.

: f ( x y -- z ) 2DUP * ROT ROT + - ;

If you know Forth this isn’t terribly difficult to parse, but just to quickly review how it works: First, ( x y -- z ) is nothing more than a comment. It does nothing in the program and is only there to help the us understand the code. 2DUP copies the top two items on the stack, so we'll have x y x y. The later x and y are then multiplied together, giving us x y p where p is the product. ROT moves the third item on the stack to the top, so after two ROTs, x y p will become p x y. Finally x and y are added together and that result is subtracted from the product.

So now we have a form of the code that is easily factorable — we can break this code up at any word break, give it a definition and, well, Bob's your Uncle. It takes zero thought to do this, since no consideration need be given to the passing of arguments. Let's give it a try just as we did before.

: g  + - ;
: f ( x y -- z ) 2DUP * ROT ROT g ;

Easy peasy, and works as expected. Of course, we should add a comment to help elucidate the signature of g.

: g ( p x y -- z ) + - ;
: f ( x y -- z ) 2DUP * ROT ROT g ;

Great! But in all fairness, this is not a very useful refactoring.

Instead, let's factor the multiply operation (*) into a function that keeps hold of its input parameters and promotes them to the top of the stack after computing the resulting product. Let's use some Unicode to give it a symbolic name. We can use ⨱ and call it "times under".

: ⨱ ( x y -- p x y ) 2DUP * ROT ROT ;

And voila! Our original example becomes a most elegant formulation:

: f ( x y -- z ) ⨱ + - ;

How cool is that! (Yeah, that’s not even a question.) If you've ever wondered why Forth eschews local variables, this is the reason! Forth is all about factoring and anything that inhibits that is undesirable.

But let's back up a moment, put our clever ⨱ factoring aside (because, in real life, how that works would have to be figured out too) and take another look at the original Forth code.

: f ( x y -- z ) 2DUP * ROT ROT + - ;

I ask you, how readable is this, really? Can you look at this code, without knowing what it was supposed to do before hand, and just "get it" almost instantaneously, like we did with the original algebraic form? Unless you are an experienced long time Forther, the answer is almost certainly: No, no you really can't. And this is about as simple as it gets!

Truth is, stack manipulation is hard. The human brain simply does not think that way.

Factoring can go a long way toward improving code readability and lessen many complex stack manipulations. But there is a limit to how much it can help. And it doesn't help much at all when one first embarks on writing a new complicated function. Factoring for complex stack manipulations is like a sport, it is an art that takes considerable effort, even after a great deal of practice. Hence why I think of it as Stack Gymnastics.

So, the next question becomes: Is there anything that can be done about it? Can we make the stack easier to work with and stack manipulating code easier to read, all without sacrificing our sacred factorability?

In the next article we'll explore the current state-of-the-art in Stack Gymnastics, albeit a rather old idea called Combinators, and see how far they can carry us.

Thanks for reading. -TS

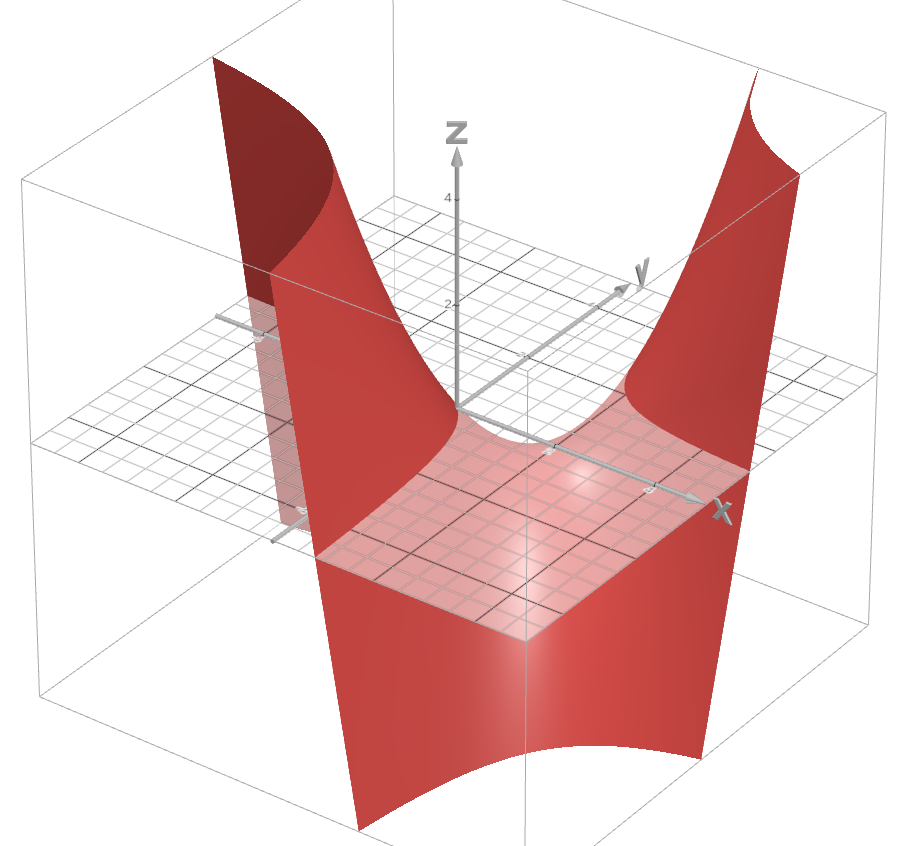
† In case you were wondering, here is a graph depicting of the overall behavior of z=(x*y)-(x+y), courtesy of Desmos 3D.