Getting Started with Reinforcement Learning with Human Feedback

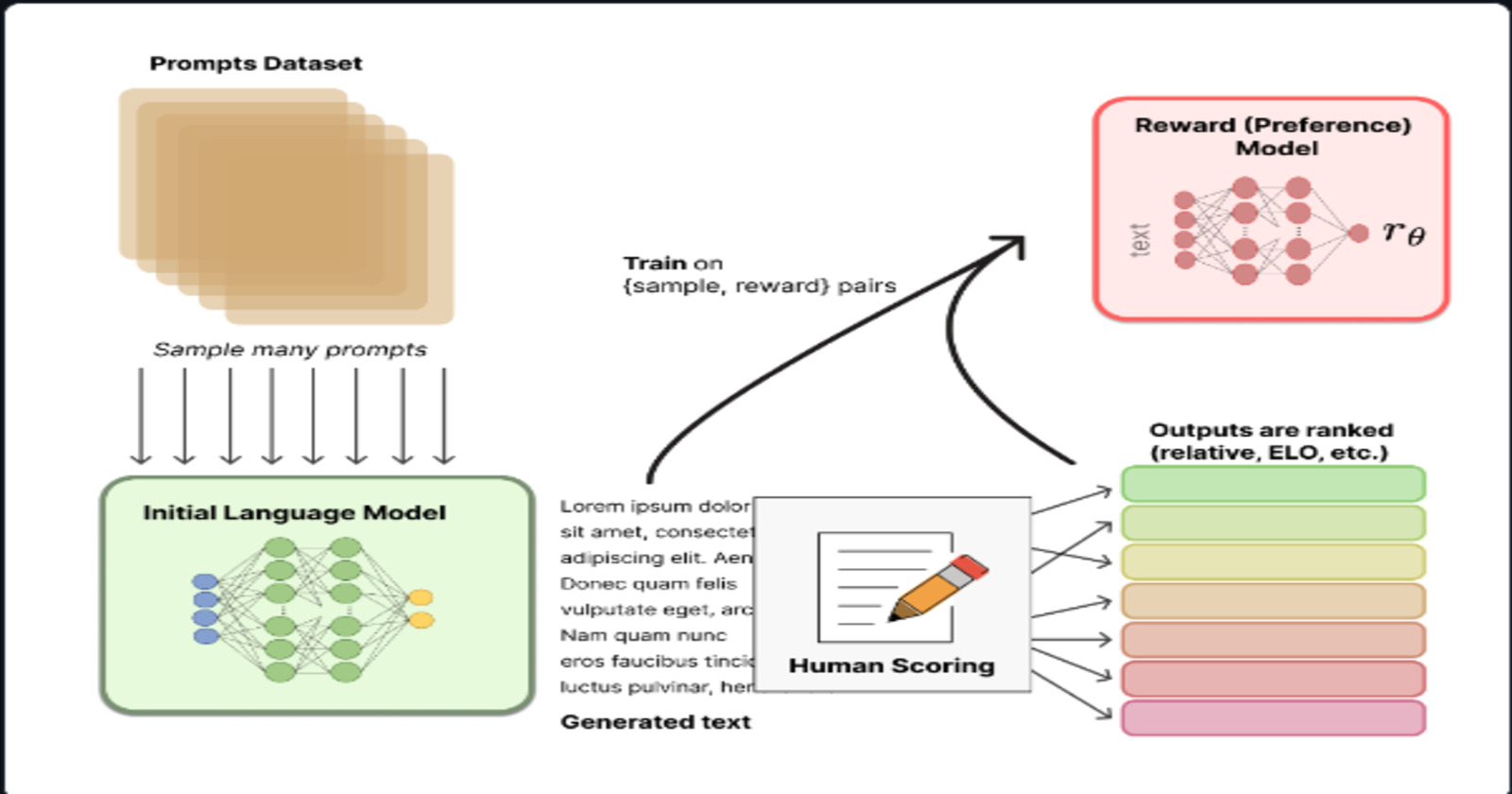
Reinforcement Learning with Human Feedback(RLHF) is a technique combined with Reinforcement learning and human feedback to better align the LLMs with human preferences. This blog covers most of the concepts that i learnt.

Before diving deep, let's understand some common RL terms and their connection to the LM.

1. Agent:- It is an entity that makes decisions, Here it is the LM itself.

2. States:- The current situation. The prompt or context to the LM.

3. Action:- It is the next step that agents takes to move to the next state. Which token can be selected as next token.

4. Reward:- It is the feedback, The LM is rewarded if the response is good.

5. Policy:- What action to take in different states, In LM, It is the distribution over the next token.

Now that we understand what RLHF is and how RL concepts relate to LLMs, let's explore the RLHF process.

Pre-trained Model

The initial model which has been trained on lots text on the web. This model has great ability for completions, but doesn’t have the ability to follow instructions.

Preparing Human Feedback Dataset

For a set of prompts use the initial model for completions and make the human rank them based on different criteria, But this process is time taking hence we create a model that chooses the right answer and gives it higher reward.

Reward Model

This reward model is trained on dataset with human feedback, and it will help score the response/completions of the model in a similar way like how the human does.

$$L_{\text{reward}} = -\log \left( \sigma(r_{\text{chosen}} - r_{\text{rejected}}) \right)$$

The reward model is a fine-tuned version of the base model, but we remove the final embedding layer and add a linear layer which outputs a single numeric value. The lesser the loss the model outputs the chosen response and vice-versa.

Derivation of the reward model loss.

The Policy Function

The goal is to train the model so that it produces responses that align with human feedback. The model generates a sequence of tokens (a trajectory) and uses the policy function to select each token.

$$J(\theta) = \mathbb{E}{\tau \sim \pi\theta}[R(\tau)]$$

After generating a response, the reward model evaluates the quality of that response. The model improves the policy such that the generating responses are much better.

Policy Gradient Estimator

The policy gradient tells us how to change/adjust the policy to increase the expected reward.

$$\nabla_\theta J(\theta) = \mathbb{E}{\tau \sim \pi\theta} \left[ \sum_{t=0}^{T} \nabla_\theta \log \pi_\theta (a_t \mid s_t) R(\tau) \right]$$

Gradient Ascent

The policy gradient tells us how to change the policy but the gradient ascent adjust’s the policy.

$$\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta)$$

The policy gradient estimator causes high variance, since we are calculating rewards for all the trajectories and there are different trajectories that are generated. To deal with there 2 variance reduction techniques as discussed below.

Variance Reduction Techniques

1. Subtracting the baseline form the reward function

$$\nabla_\theta J(\theta) = \mathbb{E}{\tau \sim \pi\theta} \left[ \sum_{t=0}^{T} \nabla_\theta \log \pi_\theta (a_t \mid s_t) (R(\tau) - b(s_t)) \right]$$

As the baseline function we can choose the value function, the value function tells us the return if you are in a particular state and follow the policy

Using advantage function in place the reward function

$$\nabla_\theta J(\theta) = \mathbb{E}{\tau \sim \pi\theta} \left[ \sum_{t=0}^{T} \nabla_\theta \log \pi_\theta (a_t \mid s_t) A(s_t, a_t) \right]$$

The advantage function measures how much better/worse taking a specific action in a given state is compared to the average value of that state.

$$A(s, a) = Q(s, a) - V(s)$$

But even after adding these variance reduction techniques, this methods can still have abnormal updating of the parameters, unstable. Hence to solve these issues we have something called as Proximal Policy Optimization(PPO).

uff, feels like there is a lot of math involved, I promise the next concept is the last, thanks for reading until now.

Proximal Policy Optimization (PPO)

PPO is a policy gradient algorithm heavily used in reinforcement learning and it is proved to simpler and stable compared to the above and other techniques. It uses clipping which helps in stable updating of the parameters.

$$L_{\text{PPO}} = \left[ L_{\text{CLIP}} - c_1 \cdot L_{\text{VF}} + c_2 \cdot L_{\text{Entropy}} \right]$$

The above is complete formula of PPO, but we will look into each part and understand, how and why it is useful.

1. L_CLIP

$$L_{\text{CLIP}} = \left[ \min \left( \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)} A_t, \text{clip} \left( \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)}, 1 - \epsilon, 1 + \epsilon \right) A_t \right) \right]$$

If the ratio of new and old policy is greater than (1 + e) then we clip the value to 1+e and similarly if it is less than (1-e) then we clip it to (1-e). Hence this can prevent the model from having large updates to the policy model and maintaining stability.

2. L_VF

$$L_{\text{VF}} = \left[ \left( V(s_t) - V_t^{\text{target}} \right)^2 \right]$$

The V_st is the current value function predicted by policy at state s. As explained above it gives the expected rewards for the state s following the current policy.
V_target is the target value, it is sum of all the rewards from the current state till the target.

3. L_entropy

$$L_\text{entropy} = \sum_{x} \pi(x) \log (x)$$

Before understanding the entropy and why do we need and why it’s important let’s understanding a concept called as reward hacking.

Reward Hacking

Imagine you’re rewarded with candy every time you say “thank you” or use other polite words. If you realize that being polite gets you more candy, you might just keep repeating those polite phrases to get more rewards.

In a similar way, language models might start to overuse certain responses if they know those responses get high rewards. To prevent this, we add something called entropy to the training process. Entropy encourages the model to try out a variety of responses, rather than just sticking to a few that are known to get rewards. This helps the model be more flexible and less predictable, rather than just repeating the same few responses.

You have reached the end of this blog/article thank you, this is my second time reading writing a blog I feel this is more like an article lol. Please feel free to leave any feedback/comments. I hope this is helpful. If you would like to connect with me I am leaving my socials.

X(twitter)

LinkedIN

References

1. https://huggingface.co/blog/rlhf

2. https://proceedings.neurips.cc/paper/2017/hash/d5e2c0adad503c91f91df240d0cd4e49-Abstract.html

3. https://www.youtube.com/watch?v=qGyFrqc34yc&t=7180s