Lovelace's Program: Part 7 - Computing the Bernoulli Numbers to an indefinite extent, from the very beginning
 Greg Alt
Greg Alt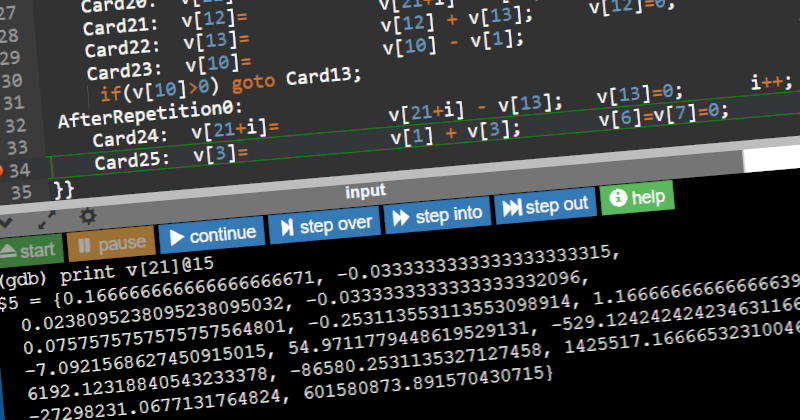
This is the seventh part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program
OK, in my last post, I got my C transliteration of Lovelace's program computing the Bernoulli Numbers to an indefinite extent but not “the very beginning”.
Lovelace's Intent: Compute "from the very beginning"
As I mentioned earlier, Lovelace very clearly told us her intent in Note G:
"It is true that if we consider our computation of B7 as a perfectly isolated calculation, we may conclude B1, B3, B5 to have been arbitrarily placed on the columns; [...] But we are not taking this view. On the contrary, we suppose the engine to be in the course of computing the Numbers to an indefinite extent, from the very beginning;"
This raises the question, aside from her assertion, how do we know that the program in the table was designed to start from B1?
If we start by looking at the table itself, there are some clues. What do the horizontal lines after Operations 7 and 12 mean? And for that matter what do those operations even do? They don’t make much sense and seem redundant. I touched on this in an earlier post, but they aren't needed when computing indefinitely starting from B5. The only purpose they serve, and why Lovelace included them, was to compute B1 and B3 as well, to compute "from the very beginning."
Let's go back to Lovelace's full explanation for Operation 7:
Operation 7 will be unintelligible, unless it be remembered that if we were calculating for n = 1 instead of n = 4, Operation 6 would have completed the computation of B1 itself, in which case the engine instead of continuing its processes, would have to put B1 on V21; and then either to stop altogether, or to begin Operations 1, 2…7 all over again for value of n(=2), in order to enter on the computation of B3; (having however taken care, previous to this recommencement, to make the number on V3 equal to two, by the addition of unity to the former n=1 on that column). Now Operation 7 must either bring out a result equal to zero (if n=1); or a result greater than zero, as in the present case; and the engine follows the one or the other of the two courses just explained, contingently on the one or the other result of Operation 7. In order fully to perceive the necessity of this experimental operation, it is important to keep in mind what was pointed out, that we are not treating a perfectly isolated and independent computation, but one out of a series of antecedent and prospective computations.
It takes a few readings of Note G to get past both the idiosyncrasies of her 19th century prose and her technical jargon that is a bit distinct from modern usage. What she calls an "experimental operation" is what we’d now call a conditional branch. We saw one flavor of this with the “here follows a repetition” loop with a conditional backwards jump.
Lovelace's Experimental Operations
Remember that her convention in this program is that:
V10 always decides which of two courses the succeeding processes are to follow, by feeling for the value of n through means of a subtraction.
In the case of Operation 7 it is a conditional forward jump. The result of the subtraction is either zero or greater than zero.
Operation 12 is the same:
Card 12 has to perform the same office as Card 7 did in the preceding section; since, if n had been =2, the 11th operation would have completed the computation of B3.
I talked about these conditional branches in my first post. These are the same as the common IF(DONE) GOTO END pattern where the DONE condition is met if previous operation's result was zero.
While the destination isn't explicit in the table, the table notation combined with the text of Note G makes it clear. Horizontal lines suggest an end, and the wrap-up Operations 24 and 25 come after the break in the table after the loop. In the text of Note G, Lovelace makes it clear that both conditional jumps have a destination of Operation 24. For different, incrementing values of n, she outlines the flow:
(1...7),(24,25).......................... gives B1 =1st number; (n being = 1).
(1...7),(8...12),(24,25)....................... B3 =2nd number; (n being = 2).
(1...7),(8...12),(13...23),(24,25)............. B5 =3rd number; (n being = 3).
(1...7),(8...12),2(13...23),(24,25)............ B7 =4th number; (n being = 4).
..............................................................................
..............................................................................
(1...7),(8...12),Σ(+1)n-2(13...23),(24,25)...B2n-1 =nth number; (n being = n).
With n =1, Operations 1-7 are executed, and then, after decrementing v10 and hitting zero, execution jumps forward to finish up with Operations 24 and 25.
For n =2, v10 is still greater than zero after Operation 7, so it continues with Operations 8-12, and then v10 is decremented to zero, so it jumps to the end.
For larger n, it continues past both of those, making one or more iterations of the main loop before hitting zero and ending the loop.
Both of these conditional branches can be represented in the C code with a simple
if(v[10]<=0) goto AfterRepetition0;
More Autoincrement Addressing
The final piece is another case of autoincrement addressing when reading the Bernoulli number result:
Card10: v[12]= v[21] * v[11];
Becomes:
Card10: v[12]= v[21+i] * v[11]; i++;
Finally, updating Card21 and Card24 to match Card10, all referencing v[21+i] uniformly. This alignment is further evidence of her intent, despite not having a notation for auto-increment indexing in the language of the table.
Running the Final Transliterated C Code
Here is the final transliterated C code:
int main() { long double v[100] = { 0 };
v[1]= 1; // [1]
v[2]= 2; // [2]
v[3]= 1; // [n]
while(1){ int i=0;
Card1: v[4]=v[5]=v[6]= v[2] * v[3]; // = 2n
Card2: v[4]= v[4] - v[1]; // = 2n-1
Card3: v[5]= v[5] + v[1]; // = 2n+1
Card4: v[11]= v[4] / v[5]; v[5]=v[4]=0; // = (2n-1)/(2n+1)
Card5: v[11]= v[11] / v[2]; // = 1/2*(2n-1)/(2n+1)
Card6: v[13]= v[13] - v[11]; v[11]=0; // = -1/2*(2n-1)/(2n+1) = A0
Card7: v[10]= v[3] - v[1]; // = n-1 (=3)
if(v[10]==0) goto AfterRepetition0;
Card8: v[7]= v[2] + v[7]; // = 2+0 = 2
Card9: v[11]= v[6] / v[7]; // = 2n/2 = A1
Card10: v[12]= v[21+i] * v[11]; i++; // = B1*2n/2 = B1A1
Card11: v[13]= v[12] + v[13]; v[12]=0; // = -1/2*(2n-1)/(2n+1)+B1*2n/2
Card12: v[10]= v[10] - v[1]; // = n-2 (=2)
if(v[10]==0) goto AfterRepetition0;
Card13: v[6]= v[6] - v[1]; // = 2n-1
Card14: v[7]= v[1] + v[7]; // = 2+1 = 3
Card15: v[8]= v[6] / v[7]; // = (2n-1)/3
Card16: v[11]= v[8] * v[11]; v[8]=0; // = 2n/2*(2n-1)/3
Card17: v[6]= v[6] - v[1]; // = 2n-2
Card18: v[7]= v[1] + v[7]; // = 3+1 = 4
Card19: v[9]= v[6] / v[7]; // = (2n-2)/4
Card20: v[11]= v[9] * v[11]; v[9]=0; // = 2n/2*(2n-1)/3*(2n-2)/4 = A3
Card21: v[12]= v[21+i] * v[11]; i++; // = B3*2n/2*(2n-1)/3*(2n-2)/3 = B3A3
Card22: v[13]= v[12] + v[13]; v[12]=0; // = A0 + B1A1 + B3A3
Card23: v[10]= v[10] - v[1]; // = n-3 (=1)
if(v[10]>0) goto Card13;
AfterRepetition0:
Card24: v[21+i]= v[21+i] - v[13]; v[13]=0; i++; // = B7
Card25: v[3]= v[1] + v[3]; v[6]=v[7]=0; // = n+1 = 4+1 = 5; by a Variable-card. by a Variable card.
}}
As before, you can run this yourself by copy/pasting into onlinegdb, putting a breakpoint at Card25, and watching as each Bernoulli number gets computed.
And that is it. Setting n to be 1, and leaving all of the Result Variables starting at 0, we get what Lovelace was intending:
B1 = 0.1666666666666667B3 = -0.0333333333333333B5 = 0.0238095238095238B7 = -0.0333333333333333B9 = 0.0757575757575758B11 = -0.2531135531135531B13 = 1.1666666666666664B15 = -7.0921568627450915B17 = 54.9711779448619529B19 = -529.1242424242346312B21 = 6192.1231884054323338B23 = -86580.2531135327127458B25 = 1425517.1666653231004602
This works, both “to an indefinite extent” and “from the very beginning”!
A Python Script to Transliterate from Table to C
Here's the simple python script to do the transliteration. It takes a .csv file of the table program as input and generates .c source output. The resulting .c file can then be compiled and run in a debugger:
import re
import csv
from word2number import w2n
import sys
# Transliterate from .csv in the language of Ada Lovelace's Note G table to the equivalent C source
# Note:
# Assumes "Data." column header is in column 10, and first input variable is in column 9
# Input "Data." variables are automatically initialized based on values in the table
# There is an assumed implicit infinite outer loop around all operations
# "Here follows a repetition of Operations" marks a backwards conditional branch (loop)
# Dashes or em-dashes in the "Number of Operation." column mark a forward conditional branch
# Extended to support auto-increment addressing: "0v21→ - 4v13" -> "v[21+i] - v[13]; i++;"
# Numbered operations are otherwise transliterated with trivial string substitutions
# Keeps processing rows until either a blank row or end of file
with open(sys.argv[1], encoding='utf-8') as csvfile:
table = list(csv.reader(csvfile))
out = ["int main() { long double v[100] = { 0 };"] # initial boilerplate, declare variables
# initialize input variables as specified in "Data."
dataRow = [row[10] for row in table].index("Data.")+1 # expect "Data." in column 10. Find the row index
for col in range(9, table[dataRow+4].index('[ ]')): # loop over data from column 9 to first empty one
var, huns, tens, ones, name = [row[col] for row in table][dataRow:dataRow+5]
out+=[f" v[{var.split('v')[1]}]= {str(100*int(huns)+10*int(tens)+int(ones))}; // {name}"]
assign = ""
out+=["while(1){ int i=0;"] # boilerplate: implicit infinite outer loop and reset autoincrement
for row in table[dataRow+5:]: # operations start right below Data input
if "".join(row) == "": # stop if detect end of table
break
rep = re.match(r" *(Here follows a repetition of Operations )([a-z\-]+) to ([a-z\-]+)\.", row[1])
test = assign.split('=')[0] # previous row's destination, if any
if rep: # jump back for loop, also add label for end
out+=[f" if({test}>0) goto Card{str(w2n.word_to_num(rep.groups()[1]))}; \n AfterRepetition:"]
elif re.match("[—-]+", row[1]): # jump forward if done, to just after next loop
out+=[f" if({test}==0) goto AfterRepetition;"]
else:
label = f"Card{str(row[1])}:" # "24" -> "Card24:"
assign = re.sub(r"\d+v(\d+),?", r"v[\g<1>]=", row[6])
assign = re.sub("]=→", "+i]=", assign) # "1v21→" -> "v[21+i]="
operation = re.sub(r"\d+v(\d+)", r"v[\g<1>]", row[5])
operation = re.sub("]→", "+i]", operation)+";" # "0v21→ - 4v13" -> "v[21+i] - v[13];"
zero = "".join([f"v[{str(x)}]=" for x in re.findall(r"v(\d+)=0", row[7])])
zero = re.sub("=$","=0;", zero) # "{ 4v13=0v13, 0v21=1v21→ }" -> "v[13]=0;"
inc = "i++;" if ("→" in "".join(row[5:7])) else "" # "i++;"
comment = f"// {str(row[8])}" # "// = B7"
# " Card24: v[21+i]= v[21+i] - v[13]; v[13]=0; i++; // = B7"
## minimal
out+=[" {0:9}{1:18}{2:19}{3:14}{4:5}{5}".format(label, assign, operation, zero, inc, comment)]
#out+=[" {0:9}{1:18}{2:19}{3:19}{4:5}{5}".format(label, assign, operation, zero, inc, comment)]
out+=["}}"] # final boilerplate
# direct forward conditional jumps to just after next loop, numbering the labels (allows multiple loops)
for n,i in enumerate(reversed([m for m,x in enumerate(out) if "AfterRepetition:" in x])):
out[0:i+1] = [re.sub(r"AfterRepetition\d*", "AfterRepetition"+str(n), s) for s in out[0:i+1]]
with open(sys.argv[1].rpartition('.')[0] + ".c", "w") as outfile:
outfile.write("\n".join(out))
How Does the Transliteration Script Work?
I'll walk you through the python script shown above.
The beginning of the script reads the .csv table into table and puts the initial C boilerplate into the list of strings, out.
The next bit of code finds the input "Data" values in the table and generates some simple C code to initialize those variables.
The "while(1)" boilerplate I mentioned in an earlier post is added to out and then the for loop iterating over rows does the bulk of the transliterating.
Rows can be one of the following:
"Here follows a repetition of Operations" loop
A horizontal line marking a conditional forward branch
The general case of an arithmetic operation on two variables
"Here follows" loops are replaced with a goto to CardN label corresponding to the number specified. I use the word2number to convert from the spelled out number words ("thirteen") to the easier to work with integer value ("13"). Also a label is added after the loop. This ensures forward jumps have a destination to jump to. These loops always test if a variable is positive and the variable tested is the last Operation's destination.
For example:
Here follows a repetition of Operations thirteen to twenty-three
becomes:
if(v[10]>0) goto Card13;
AfterRepetition0:
Horizontal lines are handled similarly, with the difference being that the conditional is always testing if the variable is zero, and the destination is fixed to be the label after the next loop, "AfterRepetition0":
if(v[10]==0) goto AfterRepetition0;
Finally, there is the general case of transliterating arithmetic operations. Aside from support for autoincrement addressing, this transliteration is trivial.
This row from the .csv table:
,6,,,-,0v13 - 2v11,1v13,"{ 2v11=0v11, 0v13=1v13 }",= -1/2*(2n-1)/(2n+1) = A0
becomes this C code:
Card6: v[13]= v[13] - v[11]; v[11]=0; // = -1/2*(2n-1)/(2n+1) = A0
Breaking it down:
The "Number of Operation", 6, is converted to the label Card6:
The "Variables receiving results", 1v13 becomes the C assignment, v[13]=
The "Variables acted upon", 0v13 - 2v11, becomes the C expression, v[13] - v[11];
Zeroing of variables is bit more complex, but handled with simple text substitution. If the prefix number is 0 in the variable name after = in "Indication of change in the value on any Variable", then the variable is zeroed out. For example the notation, 2v11=0v11, becomes the C statement, v[11]=0;
The "Statement of Results" column becomes a C end of line comment by prepending //: // = -1/2*(2n-1)/(2n+1) = A0
Finally, in order to support the autoincrement addressing Lovelace assumed and detailed in the text of Note G, I made a minor extension to the table language. Adding an arrow, →, after a variable indicates this increment. This follows Lovelace's specification in Note G, "Operation 21 always requiring its factor from a column one in advance of that which it used the previous time, and Operation 24 always putting its result on the column one in advance of that which received the previous result"
For example,
,24,,,-,0v21→ - 4v13,1v21→,"{ 4v13=0v13, 0v21→=1v21→ }",= B7
becomes:
Card24: v[21+i]= v[21+i] - v[13]; v[13]=0; i++; // = B7
Note the use of v21→ in the .csv table, and the appended +i and i++; in the resulting C code.
Following along in the python script, after the for loop iterating on rows, a final boilerplate of }} is added to close the infinite while(1) loop and the main() function.
The final bit that modifies the "AfterRepetitionN" labels isn't required for Lovelace's program, as her program only has one "Here follows" loop. This python code fixes up the number following AfterRepetition labels. The first loop will use AfterRepetition0. The next, AfterRepetition1, and so on. The forward conditional jumps then jump to just after the very next loop.
Lovelace didn't give a full specification for how this would work generally, so I just chose the simplest general semantics consistent with Lovelace's code.
The Adjusted Table
Here is the adjusted version of the table that allows "Computing the Bernoulli Numbers to an indefinite extent, from the very beginning". Cells changed from the original transcription are highlighted:
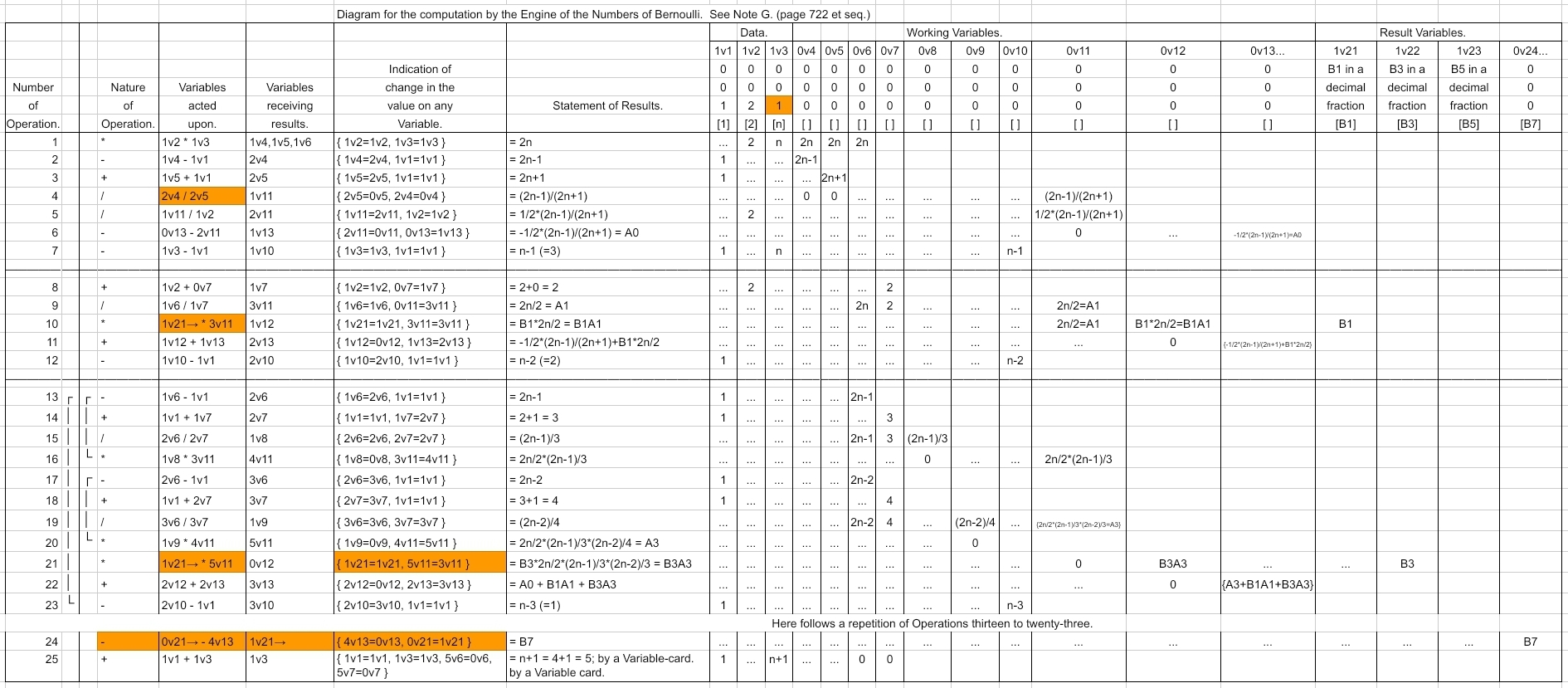
Table Changes Required for "Computing the Bernoulli Numbers to an indefinite extent, from the very beginning"
Lovelace's table required a few changes, but after those, it was possible to run her code as intended, indefinitely and from the beginning, using a simple mechanical transliteration to C.
You can compare the spreadsheet pages linked above, but to summarize, the changes were:
The Data value for v3 is set to 1, to compute "from the beginning"
Card4: Fixed a typo error, transposing v[5] and v[4] to match the comment
Card24: Fixed a bug by subtracting v[13] from v[24] instead of adding
Cards 10,21,24: adjust autoincrement variables to v21→ (changing from v22 on Card21 and v24 on Card24)
As I've mentioned in past posts, the transposition on Card4 appears to be a typographical mistake in publishing, while the missed negation on Card24 appears to be a bug due to Lovelace. This is made clear by the fact that her text description in NoteG has the same math error: "transfer the value which is on V13 to V24"
Lastly, a change is required on the cards (10, 21, and 24) reading from or writing to the resulting Bernoulli numbers. I added an arrow to indicate autoincrement addressing. I also adjusted the variable numbers that had a hardcoded offset baked in. This isn't a bug so much as a limitation in the language of the table.
Lovelace mentions in correspondence that she was trying to be diplomatic about this feature that Babbage acknowledged would be supported. Autoincrement addressing is essential for Lovelace's program, but at the time of writing he had neither added it to his design of the Analytical Engine nor come up with an extension of the table language to indicate it. As a workaround, Lovelace documented the expected operation precisely and extensively in her per-operation discussion in Note G. This would have been enough for a human to correctly punch cards based on the anticipated hardware design.
What Next?
At this point, the table runs as Lovelace intended, after transliterating to C and then compiling to an executable for a modern computer. No further changes to the table are required to run it.
There are, though, some notable typos in the rest of the table that don’t impact computation, and Card25 missed zeroing v11 which would be a bug on the Analytical Engine. In a later post I will fully itemize these other changes, gathered from other sources along with a few of my own.
But first, I will continue investigating the remaining goal of Lovelace’s.
As I mentioned in my last post, the C “long double” type doesn’t quite compare to the Analytical Engine’s proposed 50 digit fixed point precision. The next step will be emulating that. Thankfully, switching from C to C++ allows using nearly identical transliterated code, just switching “long double” to be a high-precision fixed point class with operator overloads.
Fixing bugs and getting code running is one thing, but high-precision fixed point will allow us to take a closer look and evaluate the final goal.
Remember the goals she laid out were:
"Compute the [Bernoulli] Numbers""to an indefinite extent": iterating to calculate Bn, Bn+1, etc. until you choose to halt the machine."from the very beginning": starting with B1."without having been worked out by human head & hands first": to at least B63.
In my next blog post, I'll switch to high-precision fixed point and see what happens when we calculate up to B63.
Subscribe to my newsletter
Read articles from Greg Alt directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
