Complexities in DSA

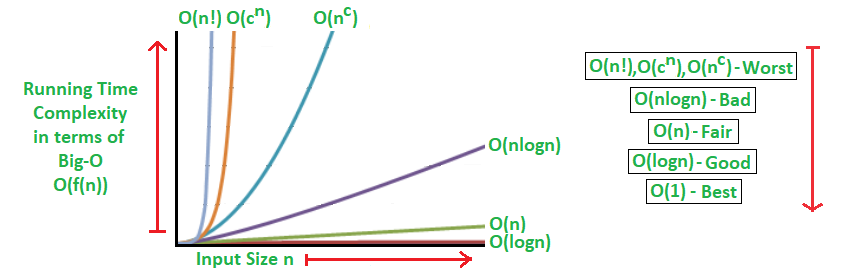
What are Complexities

One of the main reasons for Data Structures and Algorithms (DSA), is to solve problems effectively and efficiently. To determine the efficiency of a program, we look at two types of complexities:

1. Time Complexity: This tells us how much time our code takes to run.

2. Space Complexity: This tells us how much memory our code uses.

Types of Complexities

1. Constant (1)

2. Logarithmic (log n)

3. Linear (n)

4. Quadratic (n²)

5. Factorial (n!)

6. Exponential (c^n)

Asymptotic Notation

To compare efficiencies of algorithms, we use what we call asymptotic notation, a mathematical tool that estimates time based on input size without running the code. It focuses on the number of basic operations in the program.

As stated above, the time is based on input size and not on the actual time it takes to process the information. This is because using the actual time won’t be fair, as different users have different hardware, different applications running or even different programming languages: which will definitely affect the speed of the operation.

There are multiple Asymptotic Notations which include (but not limited to):

1. Big-O (O)

2. Omega (Ω)

3. Theta (θ)

4. Little-o

5. Little-omega

For this article, we are only going to be looking at the three major ones which are:

• Big-O

• Omega

• Theta

Worst Case - Big-O notation

The most commonly used notation for code analysis is Big O Notation, providing an upper limit or upper bound on the running time or memory usage concerning the input size.

You may ask, why start with the worst case scenario? Well that is because, when designing systems, you will want to go with a solution where even at the worst possible case, it still performs well.

Mathematically, the Big-O notation is expressed as:

O (g(n)) = {f(n): there exist positive constants c and n₀ such that f(n) ≤ c\g(n) for all n ≥ n₀}.*

This means that

f(n) = O(g(n)), If there are positive constants n₀ and c such that, to the right of n₀ the f(n) always lies on or below c\g(n).*

By using big O- notation, we can asymptotically limit the expansion of a running time to a range of constant factors above and below. It is a model for quantifying algorithm performance.

Best Case - Omega

Omega notation represents the lower bound of the runtime of an algorithm. It gives the best-case complexity of an algorithm.

It is defined as the condition that allows an algorithm to complete statement execution in the shortest amount of time.

Mathematically, this is represented as:

Ω (g(n)) = {f(n): there exist positive constants c and n₀ such that 0 ≤ c\g(n) ≤ f(n) for all n ≥ n₀}.*

This means that,

This means that, f(n) = Ω(g(n)), If there are positive constants n₀ and c such that, to the right of n₀ the f(n) always lies on or above c*g(n).

Average Case - Theta Notation

Mathematically, it is represented as

Θ (g(n)) \= {f(n): there exist positive constants c₁, c₂ and n₀ such that 0 ≤ c₁ g(n) ≤ f(n) ≤ c₂ g(n) for all n ≥ n₀}

This means,

f(n) = Θ(g(n)), If there are positive constants n₀ and c such that, to the right of n₀ the f(n) always lies on or above c₁*g(n) and below c₂*g(n).

Steps To Calculate Complexity in Big-O

1. Sum up all the complexities of the operation.

2. Find the fastest growing term in the function.

3. If the fastest growing term has a coefficient, remove it.

Note the following:

1. Assignments have constant time O(1)

2. Return statements have constant time.

3. Mathematical operations like addition, subtraction, division and multiplication all have constant times: O(1).

4. Loops have linear time O(n).

5. When there is an operation in a loop, the time complexity of the loop is n*(complexity of inner operation). For this reason, if you have a for loop inside another for loop, the time complexity will be n*n=n². That will give a quadratic time complexity: O(n²).

As time goes on and as we look at different data structures and algorithms, we will analyze the complexities of the different operations that can be done on these data structures and the time complexities of different algorithms as well.

For a more comprehensive guide to complexities, you can check out this article on GFG. https://www.geeksforgeeks.org/complete-guide-on-complexity-analysis/