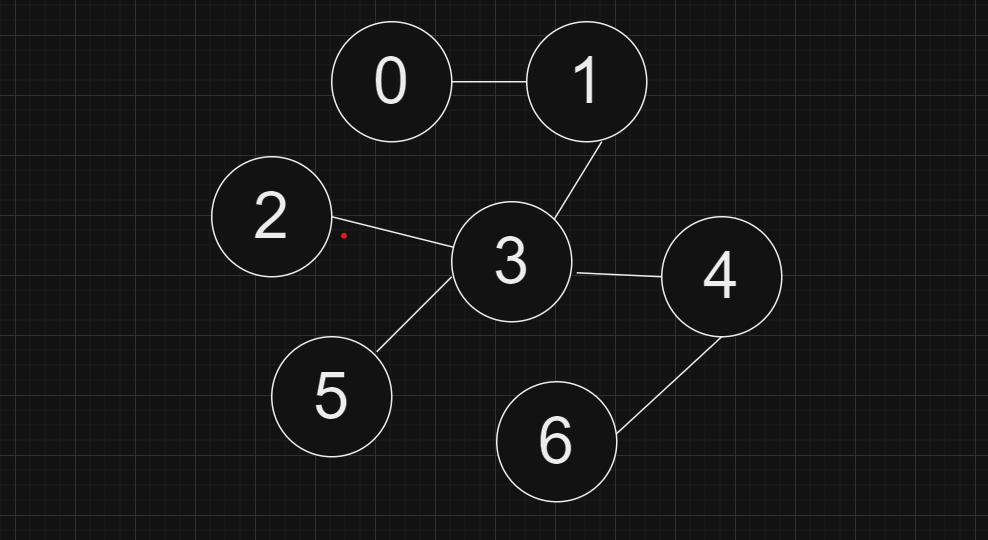
Terminologies

• Graph : In DSA generally Graph means set of nodes which are connected to each other (not necessarily). A graph can be collection of nodes which are not connected to each other(disjoined graph). The graph is composed of Vertex and Edges.

• Vertex : Generally the nodes of the graph is known as vertices.

• Edges : Edges are the link or bridge which connect two or more nodes with each other.

• Adjacency Matrix : It’s a form of Graph representation where we use n*n matrix to represent a graph. n→ number of vertices

DFS (Depth-first-search):

DFS is algorithm which we can use to traverse our graph. And as the name suggest we go to depth of the node until we reach at the final end and then we traverse back to visit the remaining nodes.

This sound like LIFO(last-in-first-out) right?

So to achieve DFS our requirement will be:

• visited[] array to keep the track of visited

• And a stack so for each new node we can add it on the and do pop it out from the top.

We can use a Stake provided by java.util or we can use a recursion stake. In this article we will be using recursion stake.

Consider this Graph:

So, for the above graph we have vertices = 7 and edges = 6.

DFS Traversal (Dry-run):

1. Start at node 0, mark visited:[0] , Stack : [0,1]

2. Move to node 1 , visited:[0,1] , stack :[0,1,3]

3. Move to node 3, visited[0,1,3], stack:[0,1,3,2]

4. Move to node 2,visited[0,1,2,3],stack:[0,1,3,4]

5. Move to node 4,visited[0,1,2,3,4],stack:[0,1,3,4,6]

6. Move to node 6,visited[0,1,2,3,4,6], stack:[0,1,3,4]

7. Stack:[0,1,3,5]

8. Move to node 5, visited[0,1,2,3,4,5,6] , stack:[0,1,3,4,5]

9. Stack:[0,1,3,4]

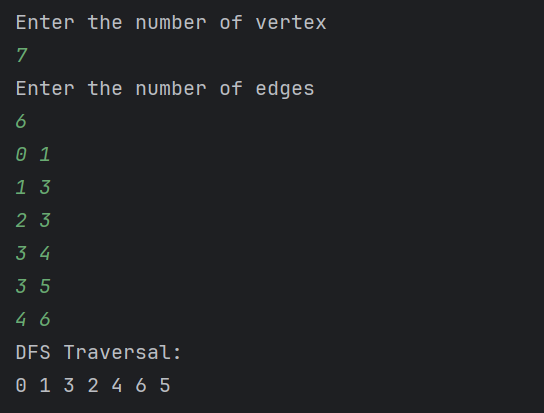
10. Since all are visited we will get empty stake at the end with the traversal result as:

    DFS: 0 1 3 2 4 6 5

public static void dfsHelper(int graph[][], boolean visited[], int node, ArrayList<Integer> arr) {
        // this function is our recursion-stake
        arr.add(node);
        for (int i = 0; i < graph.length; i++) {
            if (graph[node][i] == 1 && !visited[i]) {
                visited[i] = true;
                dfsHelper(graph, visited, i, arr);
            }
        }
    }

    public static void dfs(int graph[][], int vertex,int source) {
        boolean visited[] = new boolean[vertex];
        Arrays.fill(visited, false);
        //marking source as visited
        visited[source] = true;
        // to store result
        ArrayList<Integer> res = new ArrayList<>();
        dfsHelper(graph, visited, source, res);
        System.out.println("DFS Traversal:");
        for (var x : res)
            System.out.print(x + " ");
        System.out.println();
    }
 public static void addMatrixNode(int graph[][], int i, int j) {
        graph[i][j] = 1;
        graph[j][i] = 1;
    }

    public static void main(String args[]) {
        //un-directed graph
        Scanner sc = new Scanner(System.in);
        System.out.println("Enter the number of vertex");
        int vertex = sc.nextInt();
        int adjacencyMatrix[][] = new int[vertex][vertex];

        System.out.println("Enter the number of edges");
        int edges = sc.nextInt();
        int temp = edges;
        while (temp > 0) {
            int i = sc.nextInt();
            int j = sc.nextInt();
            addMatrixNode(adjacencyMatrix, i, j);
            temp--;
        }
        dfs(adjacencyMatrix, vertex,0);
    }

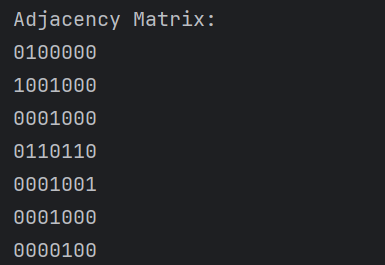
Adjacency Matrix :

Our Adjacency matrix will look something like this :

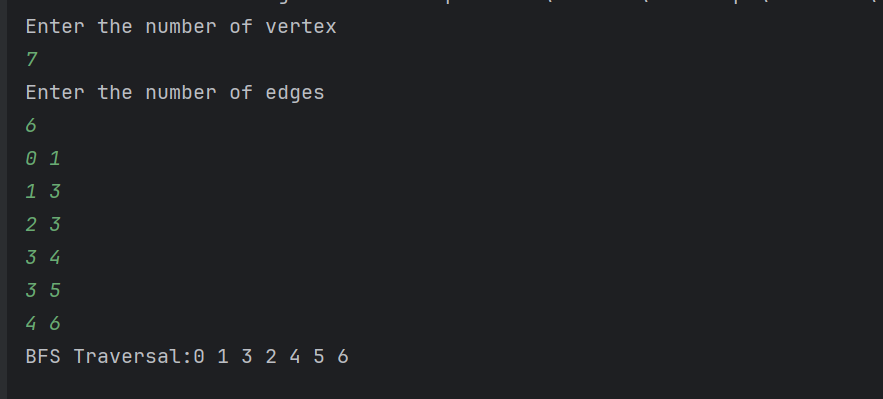
Output:

BFS(Breadth-first-search)

Similar to DFS , BFS is also a algorithm which we can use for traversal of the graph. In BFS we do level-order traversal i.e. we visit all the connecting nodes of the current node and then move to next node and then again visit all it’s neighbor.

To achieve this we use a Queue. To manage the order in which the nodes are visited since the Queue use FIFO(First-in-first-out) Principle.

BFS Traversal(Dry-Run):

Move to node 0 , visited[0], Queue[0,1]

Move to node 1, visited[0,1],Queue[1,3]

Move to node 3,visited[0,1,3],Queue[3,2,4,5]

Move to node 2,visited[0,1,2,3],Queue[2,4,5]

Move to node 4 , visited[0,1,2,3,4],Queue[4,5,6]

Move to node 5,visited[0,1,2,3,4,5],Queue[5,6]

Move to node 6,visited[0,1,2,3,4,5],Queue[6]

And we get the empty Queue at the end with traversal result as :

0 1 3 2 4 5 6

So if we consider the above graph we can write the code for it as:

public static void bfs(int graph[][], int vertex, int source) {
        boolean visited[] = new boolean[vertex];
        Queue<Integer> queue = new LinkedList<>();
        queue.add(source);
        visited[source] = true;
        //BFS using queue
        System.out.print("BFS Traversal:");
        while (!queue.isEmpty()) {
            int curr = queue.poll();
            System.out.print(curr + " ");
            for (int i = 0; i < vertex; i++) {
                if (graph[curr][i] == 1 && !visited[i]) {
                    visited[i] = true;
                    queue.add(i);
                }
            }
        }
        System.out.println();
    } 
public static void addMatrixNode(int graph[][], int i, int j) {
        graph[i][j] = 1;
        graph[j][i] = 1;
    } 
public static void main(String args[]) {
        //un-directed graph
        Scanner sc = new Scanner(System.in);
        System.out.println("Enter the number of vertex");
        int vertex = sc.nextInt();
        int adjacencyMatrix[][] = new int[vertex][vertex];

        System.out.println("Enter the number of edges");
        int edges = sc.nextInt();
        int temp = edges;
        while (temp > 0) {
            int i = sc.nextInt();
            int j = sc.nextInt();
            addMatrixNode(adjacencyMatrix, i, j);
            temp--;
        }
        bfs(adjacencyMatrix,vertex,0);
    }

Output: