Hello to all ! So I recently happened to come across some material about cryptography that caught my attention.
With the intention of making them understandable to all, I intend to begin a blog series on various cryptography principles as well as other fascinating mathematical ideas applied to cybersecurity and technology in general. This will be the first post in the series, in which we will learn about elliptic curve cryptography.

What exactly is this ECC, and why is it worthwhile to read? In actuality, the discrete logarithm problem—which is challenging to solve—is what makes ECC so secure. However, what does that actually mean? Alright, let's put it simply.

So, In ECC, the relationship between a private key and a public key is expressed as:

K = r * G

Here:

r is the private key (a randomly generated number).
G is a special point on the elliptic curve, known as the generator point.
K is the public key.

The operation * is called elliptic curve multiplication. Now, here’s the important part: unlike normal multiplication, we can’t just “divide” the public key K by G to find the private key r. This one-way function is what makes ECC so secure.

What Exactly Is an Elliptic Curve?

An elliptic curve follows an equation of the form:

y2=x3+ax+b

where a and b are constants. The curve is smooth and non-singular, meaning there are no sharp points or breaks in it. For the curve to work properly in cryptography, the discriminant (Δ\DeltaΔ) must not equal zero:

Δ=−16(4a3+27b2)

The public key is any point on this curve, and the corresponding private key is generated by multiplying the generator point GGG with the private key through elliptic curve multiplication.

Why Can’t We Just Reverse the Process?

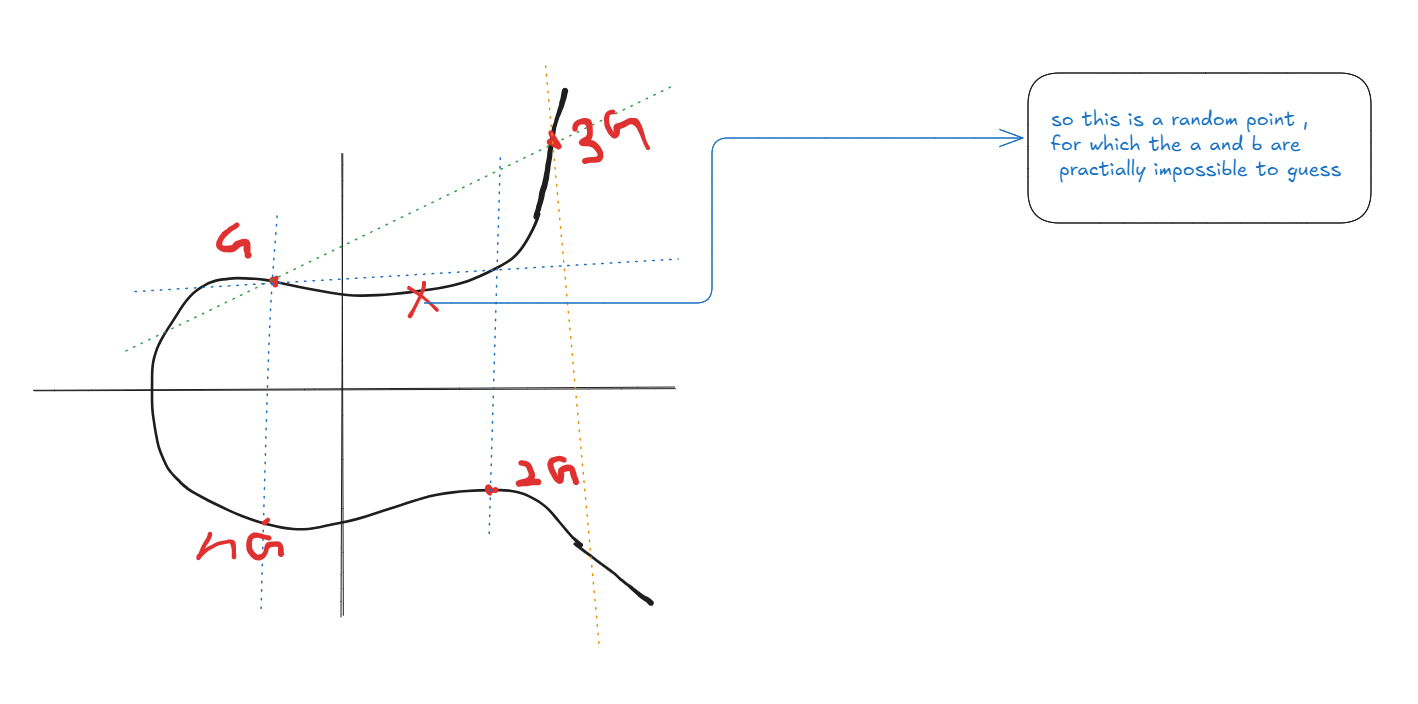
🖼️img 1 . elliptic curve

👀 Let’s look at a visual representation of an elliptic curve. Imagine a random point on this curve—let’s call it X. This point could represent a private key, but there’s no way to figure out what that private key is unless we know the generator point G and how many times it was multiplied. Even with powerful computers, this is practically impossible to compute.

To make it clearer, here’s what a point on an elliptic curve might look like:

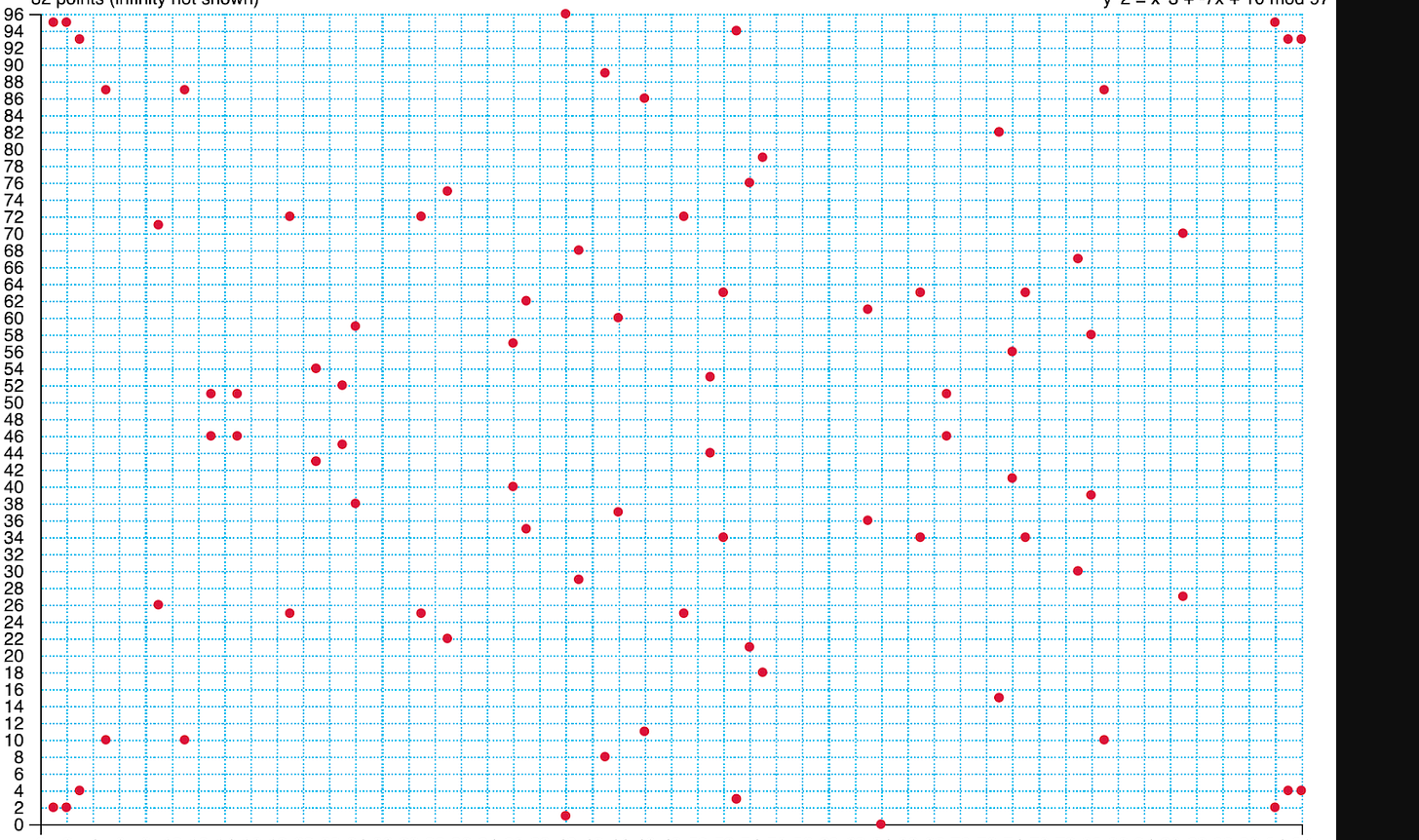
🖼️img 2. representation of points in Elliptic Curve Cryptography

Q=(49790390825249384486033144355916864607616083520101638681403973749255924539515,59574132161899900045862086493921015780032175291755807399284007721050341297360)

In this case, the first part is the x-coordinate, and the second part is the y-coordinate of the point.

Why Use Elliptic Curve Cryptography?

You might wonder, “Why use ECC when there are other cryptographic algorithms out there?” The reason is that ECC provides the same level of security with much smaller key sizes. For example, in Diffie-Hellman cryptography, you might need a 3000-bit key for a certain level of security. In ECC, you can achieve the same level with just a 256-bit key!

How Elliptic Curve Addition Works

One of the fascinating things about elliptic curves is how points are added together. Let’s say we have two points on the curve, G and 2G. The sum of these points, 3G, is found by drawing a line between G and 2G. This line will intersect the curve at exactly one additional point, which will give us 3G.

To get any point nG (refer img 1), we just repeat this process. And here’s the catch: even if you know nG you can’t work backwards to figure out what n was—that’s the core of the discrete logarithm problem.

Special Case: The Point at Infinity

There’s a special case where the line between two points becomes vertical. When this happens, the result is called the point at infinity, which acts like zero in regular arithmetic. In other words, adding the point at infinity to any other point on the curve leaves the point unchanged.

Public Key Generation

Let’s bring it all together. Say you start with a private key, rrr, which is just a randomly generated number. To generate the public key KKK, you multiply the private key by the generator point GGG:

K=r * G

The generator point G is part of a standard called secp256k1, which is used in many cryptographic systems, including Ethereum. Since G is the same for everyone, multiplying any private key r by G will always give you the same corresponding public key K.

However, even though there’s a fixed relationship between r and K, you can only calculate K from r. There’s no way to go backwards from K to r, thanks to the discrete logarithm problem we talked about earlier. This is why you can safely share your public key (and Ethereum address), without worrying about someone figuring out your private key.

Wrapping It Up

Elliptic Curve Cryptography might sound complicated, but its brilliance lies in how it simplifies security. With smaller keys and stronger encryption, ECC is a powerful tool in modern cryptography. And now, you know how it all works!
In part 2 , we will look into the higher mathematics behind how this cryptography works under the hood .
So stay tune !

Elliptic Curve Cryptography (Part 1)