Data Structures and Algorithms Unfolded: KMP, Rabin-Karp and Manacher Through My Lens (Series 1)

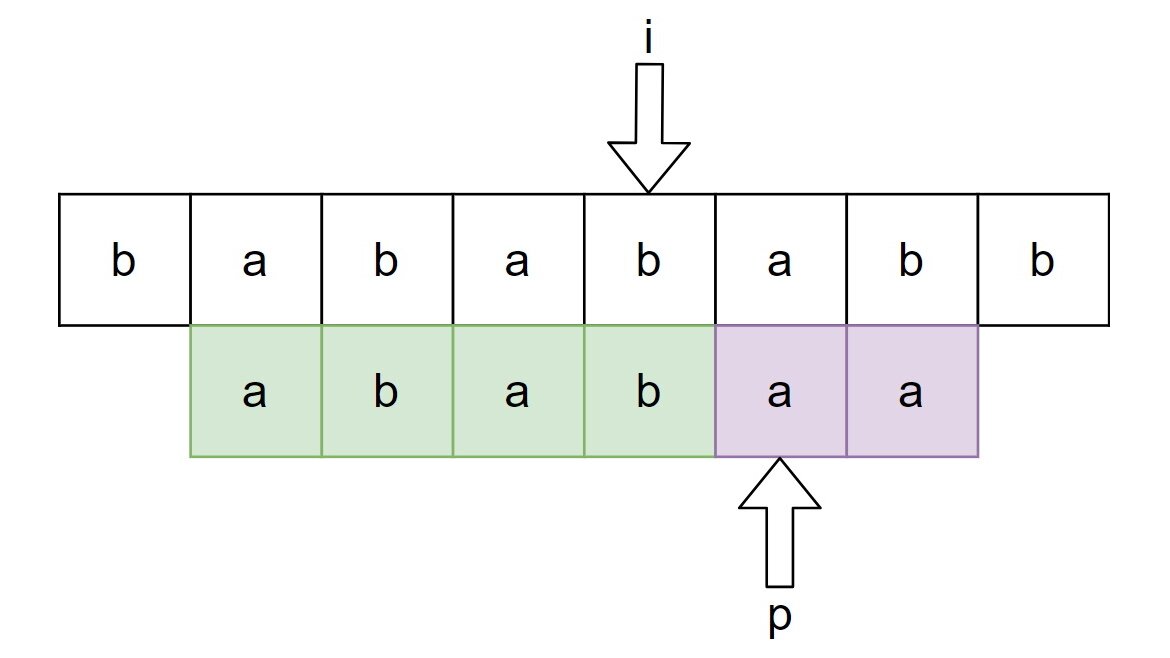
KMP Algorithm: Making Pattern Matching Less of a Wild Goose Chase

Imagine you’re trying to find your lost cat in a large city. You can’t just walk up to every cat on the street and ask, “Are you mine?” You need a strategy. That’s where Knuth-Morris-Pratt (KMP) Algorithm comes into play for strings. KMP makes sure you don’t wander aimlessly in the city of characters. It’s a pattern-matching algorithm that ensures you're not re-checking every street corner you’ve already passed.

We’ll explore KMP in this episode and explore the others in the subsequent episodes.

Now, why does KMP matter?

The Backstory

Let’s rewind to the old-school brute-force method for pattern matching. You have a text and a pattern, and you slide the pattern over the text, comparing each character one-by-one. The problem? Every time there’s a mismatch, you start all over again from the next character. If the pattern has lots of repetitive prefixes, that’s like constantly walking in circles looking for your cat—pure frustration.

KMP is the algorithm that lets you skip all the redundant checking. It uses something called an LPS array (Longest Prefix which is also Suffix). Think of it like your map of the city: whenever you hit a dead end (a mismatch), you don’t go back to the start, you skip ahead to the next promising area.

The Intuition: How Does It Work?

At the core of KMP is the idea of avoiding unnecessary comparisons. KMP pre-processes the pattern to figure out which parts of it can be reused when mismatches happen. It builds this nifty array—the LPS array—that holds information about how much of the current match can be preserved even after a mismatch.

Here’s where the magic happens: say you’re matching a pattern like ababc against some text. If you get to a point where the first few characters match, but then things fall apart, you don’t have to go back to the very beginning. Instead, KMP says, “Wait, we’ve already seen part of this before, so let’s jump forward to the part of the pattern where things were last going well.” It's like realizing that you checked a neighborhood earlier and your cat wasn’t there, so you avoid it and move on to the next.

Let’s get more technical.

Building the LPS Array: Your "Cheat Sheet" for Skipping

Before KMP starts its search, it creates the LPS (Longest Prefix Suffix) array for the pattern. The LPS array holds values that tell the algorithm how much to skip when a mismatch occurs. It’s like leaving notes at the corners of the city: “Already checked this block, no need to go back!”

For example, in the pattern "ababc", the LPS array helps KMP realize that when it matches "abab" and hits a mismatch, it doesn't need to start from the first "a" again. Instead, it can skip straight to the point where "ab" is already matched.

Here’s a visualization of what happens:

Pattern = 'ababc'  
LPS array = [0, 0, 1, 2, 0]

The 0 means no skipping, but the 1 and 2 show that if we have a partial match, we can jump forward. The array tells us to jump back to positions in the pattern that were partially matched earlier, avoiding the unnecessary grind of starting from scratch.

Below is the python script to generate lps array

def buildPrefixTable(pattern):
    lps = [0] * len(pattern)
    length = 0  # length of the previous longest prefix suffix
    i = 1
    while i < len(pattern):
        if pattern[i] == pattern[length]:
            length += 1
            lps[i] = length
            i += 1
        else:
            if length != 0:
                length = lps[length - 1]
            else:
                lps[i] = 0
                i += 1
    return lps

The process might seem like preparing for a complicated treasure hunt, but once you have the LPS array, searching for the pattern becomes incredibly efficient.

The Actual Search: Hunting with Precision

Once the LPS array is ready, KMP is all set to search for the pattern in the text. The search runs in O(n) time because every time a mismatch happens, it skips over unnecessary comparisons using the LPS array.

This way, when you hit a mismatch while trying to match the pattern "ababc" against text, KMP can cleverly skip the already-checked sections and continue the search, much like how your brain skips over irrelevant information once you have enough experience.

Here’s the actual search function:

def kmpSearch(text, pattern):
    lps = buildPrefixTable(pattern)
    i = 0  # index for text
    j = 0  # index for pattern

    while i < len(text):
        if pattern[j] == text[i]:
            i += 1
            j += 1

        if j == len(pattern):
            print(f"Pattern found at index {i - j}")
            j = lps[j - 1]
        elif i < len(text) and pattern[j] != text[i]:
            if j != 0:
                j = lps[j - 1]
            else:
                i += 1

When a match is found, KMP doesn’t stop right there. It continues searching because there could be multiple occurrences of the pattern. It's like finding your cat and then realizing there’s another cat that looks just like it—better check all of them, right?

Why KMP Is Like a Ninja

KMP feels like the ninja of pattern matching algorithms. It quietly works in the background, optimizing searches without anyone noticing. It’s efficient, it’s slick, and it’s effective at finding patterns with minimal effort. No wasted movements, no unnecessary steps.

Think of KMP like that moment when you’re writing code, and you suddenly remember that there’s a faster way to solve the problem. It’s that burst of clarity when you know exactly how to move forward without retracing all your steps. And believe me, this kind of insight is just as satisfying in code as it is in life.

When Should You Use KMP?

KMP shines in scenarios where you're dealing with patterns that could have repetitive prefixes. DNA sequence matching, spam detection, and even finding specific words or phrases in large documents are all places where KMP makes a difference.

However, if your pattern is random with no repetitive structures, KMP’s power may not shine as brightly. But when the stars align—watch out. KMP will save you both time and computing power.

Final Thoughts on KMP

In the world of algorithms, KMP stands out as one of the most clever and strategic approaches to pattern matching. It doesn’t brute-force its way through the text; instead, it calculates where to skip based on previous knowledge—like a seasoned traveler with a well-worn map.

If KMP were a character, it would be that detective who solves crimes before anyone else even knows there’s a case to solve. It’s smart, slick, and always one step ahead.

If you are interested in the finite automata of kmp please refer to KMP automata in UCI

Stay tuned for our next episode in this series - Rabin-Karp algorithm using rolling hash, which is also another ninja in string manipulation