In the world of deep learning and computer vision, image compression plays a crucial role in efficient data storage and transmission. Today, we’ll dive into a fascinating project called NormCompressAI, which explores how different mathematical norms affect image compression using autoencoders.

Project Overview

NormCompressAI aims to compress images using a deep learning model (specifically, an autoencoder) and apply various norms (L1, L2, and L-infinity) as loss functions to measure reconstruction error. The project evaluates how these norms impact the quality and efficiency of the compression.

The Dataset: CIFAR-10

For this project, we’ve chosen the CIFAR-10 dataset. It’s a collection of 60,000 32x32 color images across 10 classes. CIFAR-10 provides a good balance between simplicity and complexity, making it an excellent starting point for our autoencoder architecture.

Implementation Details

The project is implemented in PyTorch, a popular deep learning framework. Here’s a breakdown of the key components:

GitHub Repository: You can find the full code for the NormCompressAI project on GitHub. Feel free to clone and experiment with different norms and datasets.

1. Autoencoder Architecture

We’ve designed a convolutional autoencoder with the following structure:

• Encoder: Three convolutional layers with ReLU activation

• Decoder: Three transposed convolutional layers with ReLU activation and a final Sigmoid layer

2. Loss Functions

The project implements three different norm-based loss functions:

• L2 Norm (Mean Squared Error): Measures the average squared difference between the original and reconstructed images

• L1 Norm (Mean Absolute Error): Measures the average absolute difference between the original and reconstructed images

• L-infinity Norm: Measures the maximum absolute difference between the original and reconstructed images

3. Training Process

The model is trained for 10 epochs using the Adam optimizer. The training loop includes:

• Forward pass through the autoencoder

• Loss calculation using the selected norm

• Backpropagation and parameter updates

Code Implementation

Below is a basic implementation of our autoencoder model using PyTorch. This model compresses and reconstructs images from the CIFAR-10 dataset. You can experiment with different norms (L1, L2, and L-infinity) by modifying the loss function.

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import argparse
import matplotlib.pyplot as plt

# Define the autoencoder architecture by inheriting from the nn.Module 
class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder, self).__init__()  # Calling the parent class constructor to initialize the module correctly
        self.encoder = nn.Sequential(
            nn.Conv2d(3, 16, 3, stride=2, padding=1),
            nn.ReLU(),
            nn.Conv2d(16, 32, 3, stride=2, padding=1),
            nn.ReLU(),
            nn.Conv2d(32, 64, 7)
        )
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(64, 32, 7),
            nn.ReLU(),
            nn.ConvTranspose2d(32, 16, 3, stride=2, padding=1, output_padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(16, 3, 3, stride=2, padding=1, output_padding=1),
            nn.Sigmoid()
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

#loss infinity function that is calculated using the formula max | x - y | 
def l_infinity_loss(output, target):
    return torch.max(torch.abs(output - target))

if __name__ == "__main__":
    # Parse command line arguments for selecting norm loss
    parser = argparse.ArgumentParser(description="Train autoencoder with specified norm loss")
    parser.add_argument('--norm', type=str, choices=['L2', 'L1', 'Linf'], default='L2', help='Select norm type (L2, L1, or Linf)')
    args = parser.parse_args()

    # Load and preprocess the CIFAR-10 dataset
    transform = transforms.Compose([transforms.ToTensor()])
    trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
    trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=2)

    # Initialize the model
    model = Autoencoder()

    # Choose loss function based on user input
    if args.norm == 'L2':
        criterion = nn.MSELoss()  # L2 norm (Mean Squared Error)
        print("Using L2 Norm Loss (MSE)")
    elif args.norm == 'L1':
        criterion = nn.L1Loss()  # L1 norm (Mean Absolute Error)
        print("Using L1 Norm Loss (MAE)")
    else:
        criterion = l_infinity_loss  # L-infinity norm (Maximum Absolute Error)
        print("Using L-infinity Norm Loss")

    # Initialize optimizer
    optimizer = optim.Adam(model.parameters())

    # Training loop
    num_epochs = 10
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    model.to(device)

    loss_values = []

    for epoch in range(num_epochs):
        epoch_loss = 0.0
        for data in trainloader:
            img, _ = data
            img = img.to(device)

            # Forward pass
            output = model(img)
            loss = criterion(output, img)

            # Backward pass and optimize
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            epoch_loss += loss.item()

        avg_loss = epoch_loss / len(trainloader)
        loss_values.append(avg_loss)

        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {avg_loss:.4f}')

    print("Training finished!")

    # Plot the loss over epochs
    plt.plot(range(1, num_epochs+1), loss_values, label=f'{args.norm} Norm Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.title(f'Training Loss using {args.norm} Norm')
    plt.legend()
    plt.show()

Results

L1 Norm:

The L1 norm, also known as Mean Absolute Error (MAE), penalizes large errors less harshly compared to L2. This tends to produce slightly blurrier reconstructions but is often more robust to outliers.

python main.py --norm L1

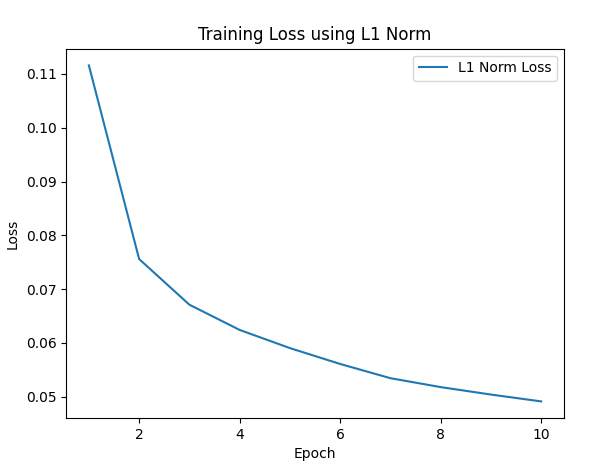
Training loss over epochs using L1 norm (MAE)

L2 Norm:

The L2 norm, or Mean Squared Error (MSE), is commonly used in image reconstruction tasks. It heavily penalizes large errors, resulting in sharper reconstructions but can be more sensitive to noise in the data.

python main.py --norm L2

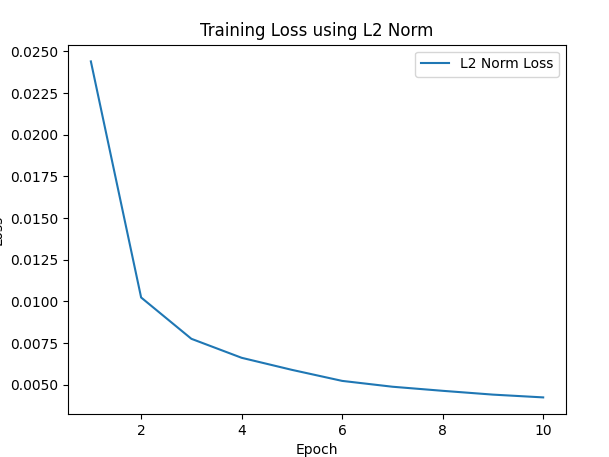
Training loss over epochs using L2 norm (MLE)

L-infinity Norm:

The L-infinity norm measures the maximum absolute error in the reconstructed image, focusing on the largest discrepancy between the original and the reconstructed images. This can be useful for applications where large individual pixel errors need to be minimized.

python main.py --norm Linf

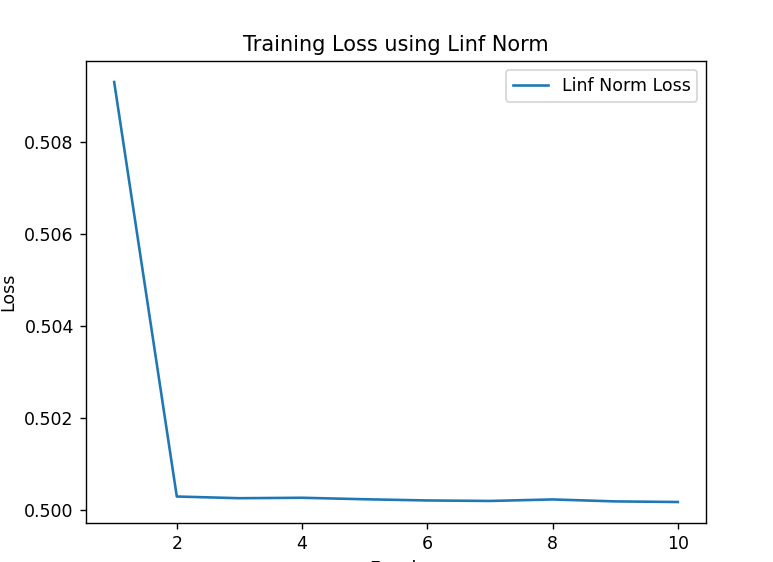
Training loss over epochs using L inf

Results and Analysis

The project provides visualizations of the training loss for each norm:

• L1 Norm: Shows a steady decrease in loss over epochs

• L2 Norm: Exhibits a similar trend to L1, but with slightly different convergence characteristics

• L-infinity Norm: Demonstrates a unique loss curve, reflecting its focus on maximum error

These results highlight how different norms can affect the learning process and potentially the quality of the compressed images.

Conclusion and Future Work

NormCompressAI provides valuable insights into the impact of different norms on image compression using autoencoders. Future work could include:

• Comparing the visual quality of reconstructed images across different norms

• Exploring hybrid loss functions that combine multiple norms

• Extending the project to higher-resolution datasets or more complex architectures

This project serves as an excellent starting point for researchers and enthusiasts interested in the intersection of deep learning and image compression. By understanding the nuances of different norms, we can develop more efficient and effective compression techniques for the ever-growing world of visual data.

Feel free to explore the full code and experiment with different norms yourself. Happy coding!