Huffman Coding Algorithm
 Sailesh
SaileshTable of contents

In this blog, we will learn about the Huffman Coding Algorithm, which uses a greedy approach to compress file storage using variable encoding schemes.
Idea
The core concept of the Huffman Coding Algorithm is to allocate fewer bits to more frequently occurring characters, utilizing variable-length codes rather than the fixed 8 bits per character. This approach addresses the inefficiency of reading each character with a uniform 8-bit length.
Consider a message with 10 e's and 2 q's, which looks like this:
eeeeeeeeeeqq
Fixed Length Encoding - Each character takes 8 bits.
So, total bits for e = 10×8 = 80 bits and for q = 2×8 = 16 bits.
This adds up to 96 bits in total.
Variable Length Encoding: We assign shorter codes to more frequent characters (in this case, 'e').
By assigning 7 bits to 'e' and 9 bits to 'q', the total bits for 'e' = 10×7 = 70 bits, and for 'q' = 2×9 = 18 bits, resulting in a total of 88 bits, which is more efficient than the previous approach.
Implementation
Consider the characters and their respective frequencies.
| Character | Frequency |
| a | 12 |
| b | 7 |
| c | 2 |
Based on the table above, the total number of characters is 21. Assuming each character is stored with a 3-bit code, the total number of bits required would be 21×3 = 63 bits.
Now, create a binary tree with each character and its frequency in each node.
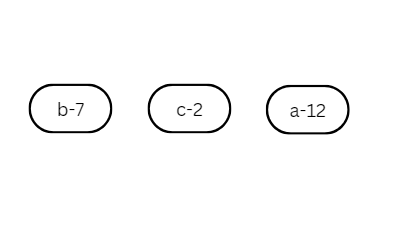
Now, select two binary trees with the smallest frequencies, connect them, and store the resulting frequency in the parent node without the character.
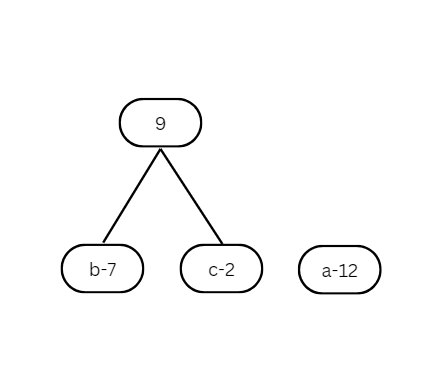
Continue this process until you have a single binary tree. The resulting tree now looks like this:
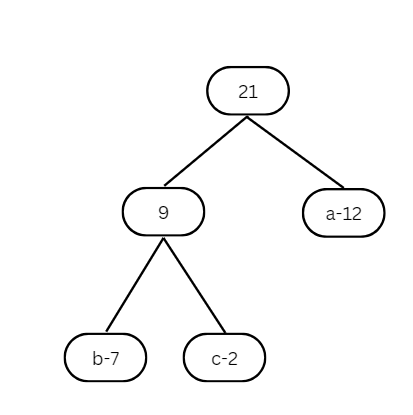
Once the tree is built, each leaf node represents a letter with a code. To find the code for a specific node, start at the root and move to the leaf node. For each move to the left, add a 0 to the code, and for each move to the right, add a 1. As a result, for the tree we generated, we get the following codes:
Character | Code | Frequency | Total Bits |
a | 1 | 12 | 12×1 = 12 |
b | 00 | 7 | 7×2 = 14 |
c | 01 | 2 | 2×2 = 4 → 30 bits |
Calculating bits saved
Initially, assuming a 3-bit code for each character, the total number of bits required was 63. However, by using the Huffman algorithm, we reduced the total to 30 bits, achieving a storage space saving of approximately 52.38%.
Applications
Huffman coding has several real-time applications, including:
File Compression: Huffman coding is widely used in file compression formats like ZIP and GZIP to reduce file sizes.
Image Compression: It is used in JPEG image compression to efficiently encode the image data.
Audio Compression: MP3 audio files use Huffman coding to compress audio data without significant loss of quality.
Data Transmission: Many communication protocols use Huffman coding to minimize the amount of data transmitted over networks.
Text Compression: It is used in text compression algorithms to reduce the size of text files by assigning shorter codes to more frequent characters.
Conclusion
In conclusion, the Huffman Coding Algorithm is a powerful and efficient method for data compression, leveraging a greedy approach to assign variable-length codes to characters based on their frequencies. By allocating shorter codes to more frequently occurring characters, Huffman coding significantly reduces the total number of bits required for storage, as demonstrated in our example. This algorithm is widely used in various real-time applications, including file, image, audio, and text compression, as well as data transmission. Its ability to minimize storage space and enhance transmission efficiency makes it an indispensable tool in the field of data compression. Understanding and implementing Huffman coding can lead to substantial improvements in storage and transmission efficiency across multiple domains.
Thanks for your time !!
Subscribe to my newsletter
Read articles from Sailesh directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
