Chapter 44: Graphs (Part 1)
 Rohit Gawande
Rohit GawandeTable of contents
- 1. Introduction to Graphs
- 2. Types of Graphs (Based on Edge)
- Types of Edges in Graphs
- Edge Weights
- Weight Characteristics
- 3. Graph Representation
- 1. Adjacency List Representation
- Adjacency List (List of Lists) - In-Depth Introduction
- Key Characteristics of an Adjacency List:
- Example Graph:
- Visualizing the Adjacency List:
- Representation in Different Data Structures:
- Benefits of Using an Adjacency List:
- Real-world Applications:
- Advantages of Adjacency List:
- Example Usage:
- Conclusion:
- 2. Adjacency Matrix Representation
- Advantages of Adjacency Matrix:
- Disadvantages of Adjacency Matrix:
- Conclusion
- 3. Edge List Representation
- 4. Implicit Graph Representation
- Summary
- Conclusion on Graph Storage Methods
- 4. Applications of Graphs
- 5. Creating a Graph (Adjacency List Implementation in Java)
- Step 1: Define the Structure of an Edge
- Step 2: Create the Graph
- Summary of Step 2
- Step 3: Add Edges
- Adding Edges Step-by-Step
- Final Adjacency List Representation
- Understanding the Relationships
- Conclusion of Step 3
- Step 4: Accessing Neighboring Vertices
- Visualizing this Access
- Why Accessing Neighbors is Important
- Diagrammatic Representation of Access
- Conclusion
- Step 5: Visual Representation of the Graph
- Step 6: Full Code
- Conclusion
- 6.Graph Traversal
- Graph Traversal Types
- 6.1 Breadth-First Search (BFS)
- Introduction to BFS
- Key Concepts
- Graph Representation
- Adjacency List of the Graph
- How BFS Works (Step-by-Step Process)
- 3. BFS Execution with Detailed Visualization
- 4. Visualizing the Visited Array with Boxes
- 5. BFS Algorithm in Java
- Code:
- Key Changes Made:
- Sample Output:
- Explanation of Output:
- 6.2 Depth-First Search (DFS)
- 8. Has Path? (Using DFS)
- Conclusion
In this chapter, we will embark on an in-depth exploration of Graphs, one of the most versatile and widely-used data structures in computer science. Graphs play a crucial role in representing relationships between entities, making them indispensable in areas such as social networks, road maps, recommendation systems, and more.
In Part 1 of this comprehensive study on graphs, we will cover the foundational concepts and practical techniques that form the core of graph theory and implementation. This chapter will equip you with a solid understanding of graph structures, their types, and applications. We will also delve into essential algorithms that help navigate and analyze graphs.
1. Introduction to Graphs
What is a Graph?
Graphs are one of the most important chapters in Data Structures and Algorithms (DSA) and are widely implemented in real-life applications by companies. A graph is a network of nodes (also known as vertices) connected by edges.In real-life scenarios, graphs are often used to model relationships or networks. For example, consider a map with different cities connected by roads. In this case, the cities represent the nodes (vertices), and the roads represent the edges connecting those nodes.
Graphs are particularly useful for calculating the shortest path between two points, which is commonly seen in GPS systems and mapping software.
Key terminology
Vertices (V): Nodes or points in a graph.
Edges (E): Links between nodes.
Degree: The number of edges connected to a vertex.
Adjacency: Relationship between two vertices connected by an edge.
Path: A sequence of vertices connected by edges.
2. Types of Graphs (Based on Edge)
Types of Edges in Graphs
Unidirectional Edge (Directed Graph):
Definition: In a directed graph, an edge has a specific direction, indicating that movement is only possible from one vertex to another.
Visual Representation:
A -----------> BCharacteristics:
Each edge is represented by an arrow.
If there is an edge from A to B, you cannot move from B to A unless there is a separate edge defined.
Example in Real Life: A one-way street in a city where vehicles can only travel in one direction.
Bidirectional Edge (Undirected Graph):
Definition: In an undirected graph, edges do not have a direction, meaning that movement can occur in both directions between vertices.
Visual Representation:
A <----------> BCharacteristics:
Edges are represented by a line without arrows.
Movement is allowed in both directions; if there is an edge between A and B, you can go from A to B and vice versa.
Example in Real Life: A two-way street that allows traffic to flow in both directions.
Edge Weights
Edges can also be classified based on whether they have weights associated with them:
Weighted Graph (Undirected):
Definition: In a weighted graph, each edge has a numerical value (weight) that represents the cost, distance, or capacity associated with traversing that edge.
Visual Representation:
A --(5)-- BCharacteristics:
The number (weight) can represent various metrics, such as distance, time, or cost.
Weighted graphs are useful in optimization problems, like finding the shortest path.
Example in Real Life: A map where the distance between cities is represented by weights on the roads.
Unweighted Graph (Undirected):
Definition: In an unweighted graph, edges do not have any associated weights, meaning all edges are considered equal in terms of cost or distance.
Visual Representation:
A -- BCharacteristics:
All edges are treated as having the same weight (usually 1 or no cost).
Useful for problems where the relative distance or cost does not matter.
Example in Real Life: A social network graph where the presence of a friendship is more important than the strength of the friendship.
Weight Characteristics
Positive Weights: Commonly used to indicate actual costs or distances.
Zero Weights: Indicates that there is no cost associated with traversing that edge. This can be useful in algorithms when you want to prioritize certain paths.
Negative Weights: While not commonly used in most practical applications, they can represent scenarios where traversing an edge results in a gain (like earning money). Algorithms like the Bellman-Ford algorithm can handle graphs with negative weights, but care must be taken to avoid negative cycles (a cycle that reduces the total weight indefinitely).
Understanding the types of edges and their characteristics is crucial for implementing algorithms that solve graph-related problems. The choice between directed and undirected graphs, as well as the use of weighted versus unweighted edges, can significantly impact the design and efficiency of graph algorithms, especially those dealing with pathfinding and network analysis.
3. Graph Representation
When we want to store a graph, we require a structure to represent it, meaning it will occupy some memory, so we have to declare how it will be stored. In essence, we need to represent the graph similar to how we store linked lists or trees. For instance, we can use the LinkedList class from the Java Collection Framework (JCF), or we can create a custom Node class, such as:
class Node {
int data;
Node next;
}
Similarly, for trees, we often define:
class Node {
int data;
Node left, right;
}
Just like this, there are many ways to store a graph. Among those, one of the most popular methods is the Adjacency List, which is used for most graph problems.
Adjacency List: This method is commonly used in various graph-related problems because of its efficiency in terms of memory usage.
Adjacency Matrix: Another way to store a graph is using an Adjacency Matrix, where we create a 2D array to represent edges between nodes.
There are also more methods like:
Edge List: A simple list of edges representing the connections between nodes.
2D Matrix (Implicit Graph): This is commonly used for problems like grids, where the graph is implicitly represented.
These structures are used based on the requirements of the problem and how efficiently we need to store and process the graph.
1. Adjacency List Representation
Adjacency List (List of Lists) - In-Depth Introduction
An Adjacency List is one of the most widely used and efficient methods for representing graphs, especially in cases where the graph is sparse—meaning it has relatively few edges compared to the number of possible connections between vertices. In an adjacency list, we represent each vertex of the graph along with a list of all the vertices it is directly connected to.
In simple terms, for each vertex, we maintain a list that stores its neighboring vertices. This is in contrast to other methods like an Adjacency Matrix, which uses a 2D array to store all possible connections (edges), regardless of whether they actually exist. The adjacency list only stores the existing edges, making it an efficient and compact representation.
Key Characteristics of an Adjacency List:
Structure: For each vertex in the graph, there is a list (or a collection) that contains the neighboring vertices. The adjacency list is thus essentially a list (or array) of lists.
Space Efficiency: In sparse graphs, where the number of edges is significantly less than the maximum possible edges, an adjacency list is highly space-efficient. It only stores actual connections between vertices, as opposed to an adjacency matrix, which allocates space for all possible edges, even if many of them don’t exist.
Dynamic Nature: The adjacency list is flexible, allowing easy insertion and deletion of edges, making it ideal for dynamic graphs where connections between vertices may change over time.
Example Graph:
Consider a graph with 4 vertices, represented visually as follows:
0 2
\ / \
1 --- 3
Properties:
Vertices (Nodes): 4 (numbered as 0, 1, 2, 3)
Edges: 4 (0-1, 1-2, 1-3, 2-3)
Type: The graph is undirected because there is no specific direction between connected nodes (e.g., 1 is connected to 3, and 3 is connected to 1 equally).
Unweighted: There are no weights assigned to the edges between vertices.
Cycle: The graph contains a cycle (0-1-3-2-0), which means there is a closed loop. This is typical in graph structures but does not happen in linear structures like linked lists, where cycles are uncommon unless specifically formed.
Graph Representation as an Adjacency List:
Now, let’s represent this graph using an adjacency list. Each node will store a list of its neighboring nodes:
Node 0 is connected to Node 1.
Node 1 is connected to Nodes 0, 2, and 3.
Node 2 is connected to Nodes 1 and 3.
Node 3 is connected to Nodes 1 and 2.
Thus, the adjacency list looks like:
0 -> [1]
1 -> [0, 2, 3]
2 -> [1, 3]
3 -> [1, 2]
This list stores each vertex's direct connections, or "neighbors," in a compact form.
Visualizing the Adjacency List:
Array of ArrayLists Representation:
In memory, the Adjacency List can be represented as an array where each index corresponds to a vertex. The value at each index is a list (or set) of neighbors for that vertex.
Array of List/Neighbors:
-------------------------
>>> [0] -> [1]
>>> [1] -> [0, 2, 3]
>>> [2] -> [1, 3]
>>> [3] -> [1, 2]
In an Adjacency List, we store information on how one node is connected to other nodes. For example, vertex 0 is connected to vertex 1, and vertex 1 is connected to vertices 0, 2, and 3.
The Adjacency List structure for this graph looks like this:
| Vertex | Neighbors List |
| 0 | [1] |
| 1 | [0, 2, 3] |
| 2 | [1, 3] |
| 3 | [1, 2] |
This list tells us which nodes each vertex is connected to, and this representation is optimal in terms of space because we only store the neighbors without any unnecessary data.
Representation in Different Data Structures:
In programming, the adjacency list can be represented using different data structures, depending on the requirements:
ArrayList<ArrayList>: This is one of the most common representations in Java, where each vertex has a list of integers (its neighbors).
Array of Lists: An array where each index corresponds to a vertex, and each element is a list of neighbors.
HashMap<Integer, List>: Instead of using arrays, a
HashMapcan be used, where the key is the vertex, and the value is a list of its neighbors. This representation is useful when the graph's vertex labels are not sequential numbers.
Among these, ArrayList<ArrayList> is the most popular for solving graph problems because it provides a flexible and easy-to-use structure.
Benefits of Using an Adjacency List:
Space Efficiency: The adjacency list only stores the existing edges, making it a more memory-efficient way to represent a graph, especially when dealing with sparse graphs.
Time Efficiency for Specific Operations:
Accessing the neighbors of a vertex takes constant time
O(1)to find the list of neighbors.Traversing all neighbors of a vertex takes
O(k), wherekis the number of neighbors.
Dynamic Updates: It’s easy to add or remove edges in an adjacency list, making it suitable for dynamic graph problems where the structure of the graph changes over time.
Real-world Applications:
Social Networks: Each person (vertex) can have a list of friends (neighbors), making the adjacency list a natural fit for representing relationships.
Road Networks: Cities or intersections can be represented as vertices, and roads connecting them as edges.
Web Graphs: Websites can be vertices, and links between them are edges.
Advantages of Adjacency List:
Memory Optimization: It avoids storing redundant information, making it ideal for graphs with fewer connections (sparse graphs).
Fast Neighbor Lookup: Given a vertex, accessing its neighbors is quick and efficient, typically
O(1)for finding the list, andO(k)to iterate through all neighbors.Simple Representation: The adjacency list directly reflects how nodes are connected, making it intuitive for visualization and problem-solving.
Example Usage:
Suppose we need to check all neighbors of vertex 1:
We look at arr[1] and get the list
[0, 2, 3], meaning 1 is connected to vertices 0, 2, and 3.This operation is performed in constant time
O(1)to access the list and linear timeO(k)to traverse it.
For most graph problems, such as traversals (DFS, BFS), shortest path algorithms (Dijkstra, Bellman-Ford), or detecting cycles, the adjacency list representation is highly useful.
Conclusion:
The Adjacency List is an efficient and scalable way to represent graphs. It offers a compact, memory-efficient structure while allowing quick access to each vertex's neighbors. This makes it particularly suited for large, sparse graphs where saving space is essential, and operations like graph traversal or neighbor look-up are frequent.
2. Adjacency Matrix Representation
An Adjacency Matrix is another common method to store graph information. It provides a way to represent a graph as a 2D matrix (a grid), where the presence of an edge between any two vertices is stored as a value in the matrix. Each row and column of the matrix corresponds to a vertex in the graph, and the entry at matrix position (i, j) indicates whether an edge exists between vertex i and vertex j.
Space Complexity
For a graph with V vertices, an adjacency matrix requires O(V²) space to store the information about the edges, regardless of how many edges are actually present in the graph. This space complexity is higher than that of an Adjacency List, where the storage is based on the number of edges.
Example Graph
Let's consider the same undirected, unweighted graph with 4 vertices and 4 edges:
0 2
\ / \
1 --- 3
Vertices (V): 4
Edges (E): 4
Graph Type: Undirected and unweighted.
Since the graph is undirected, if there's an edge between vertices i and j, the same edge exists between j and i. Therefore, the adjacency matrix will be symmetric along the diagonal.
Adjacency Matrix Representation
To represent this graph as an adjacency matrix, we create a 4 x 4 matrix (because there are 4 vertices). Both the rows and columns of the matrix represent the vertices of the graph. Here's how the matrix looks, with the vertices labeled:
| Vertex | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
Here’s what this matrix means:
The entry at position
(i, j)represents whether there is an edge between vertexiand vertexj.A
1in the matrix indicates that an edge exists between the two vertices, while a0indicates no edge.The diagonal entries
(i, i)are all0because there are no self-loops (no vertex is connected to itself).
For example:
matrix[0][1] = 1means there is an edge between vertex0and vertex1.matrix[2][3] = 1means there is an edge between vertex2and vertex3.matrix[0][2] = 0means there is no direct edge between vertex0and vertex2.
Searching for an Edge in an Adjacency Matrix
To check whether an edge exists between two vertices i and j, you can simply look at the entry matrix[i][j]. If the value is 1, then the edge exists; if it is 0, the edge does not exist. Since accessing a specific entry in a matrix is a constant-time operation, checking the presence of an edge takes O(1) time.
For example:
To check if there's an edge between vertex
1and vertex3, look atmatrix[1][3]. If it's1, the edge exists.The matrix is symmetric, so
matrix[1][3]andmatrix[3][1]will both give the same result.
Time Complexity for Finding Neighbors
Unlike an adjacency list, where finding the neighbors of a vertex is efficient (limited to the number of edges), finding the neighbors of a vertex in an adjacency matrix takes O(V) time. This is because you need to check every entry in the corresponding row (or column) of the matrix to determine which vertices are connected.
For example, to find the neighbors of vertex 1, you need to examine all entries in row 1 of the matrix:
matrix[1][0] = 1, so vertex1is connected to vertex0.matrix[1][1] = 0, so no self-loop.matrix[1][2] = 1, so vertex1is connected to vertex2.matrix[1][3] = 1, so vertex1is connected to vertex3.
Thus, the neighbors of vertex 1 are vertices 0, 2, and 3, but it takes O(V) time to determine this.
Weighted Graphs in Adjacency Matrix
In the case of weighted graphs, we can store the edge weights in the matrix instead of just using 0 and 1. In this case:
matrix[i][j] = weight indicates the weight of the edge between vertex
iand vertexj.matrix[i][j] = 0 (or a large value like
∞) means no edge exists between the vertices.
For example, if the edge between vertex 1 and vertex 2 has a weight of 5, the matrix entry would be matrix[1][2] = 5.
Advantages of Adjacency Matrix:
Simple to Implement: The adjacency matrix is straightforward to implement and understand.
Constant Time Edge Lookup: Checking whether an edge exists between two vertices takes constant time O(1).
Suitable for Dense Graphs: In dense graphs, where the number of edges is close to the maximum number of possible edges (close to
V²), the adjacency matrix can be more efficient than an adjacency list.
Disadvantages of Adjacency Matrix:
Space Complexity: The adjacency matrix requires O(V²) space, even if the graph is sparse and contains few edges. This makes it inefficient for large, sparse graphs.
Time Complexity for Neighbors: Finding all neighbors of a vertex takes O(V) time, which can be slow if the graph has a large number of vertices.
Unoptimized for Sparse Graphs: Since space is allocated for all possible edges, even for those that don’t exist, the adjacency matrix is inefficient when the graph has very few edges compared to the number of vertices.
Conclusion
The Adjacency Matrix is a simple and easy-to-understand way of representing a graph, where all vertex connections are stored in a 2D matrix. While it allows for quick edge look-up in constant time, it can be inefficient in terms of space and neighbor-finding time, especially for large sparse graphs. Despite these drawbacks, the adjacency matrix is still useful for dense graphs and when constant-time edge look-up is critical.
3. Edge List Representation
An Edge List is one of the simplest ways to represent a graph. Instead of using a matrix or a list to store connections between nodes, the edge list just stores all the edges in the form of pairs (u, v), where u and v are vertices connected by an edge. If the graph is weighted, we also include the weight of the edge, forming a triplet (u, v, weight).
Characteristics:
Structure: The edge list is simply a collection (array or list) of edges. Each edge is a pair or triplet.
Space Complexity: The space used is proportional to the number of edges
O(E).
Example Graph:
0 2
\ / \
1 --- 3
In this graph:
Vertices: 4
Edges: 4, represented as a list of pairs:
{(0, 1), (1, 2), (1, 3), (2, 3)}.
If the graph is weighted, each edge will also have a weight:
{(0, 1, 2), (1, 2, 3), (1, 3, 1), (2, 3, 5)}.
Here, the edge between vertex 0 and vertex 1 has a weight of 2.
Edge List Visualization:
Unweighted Edge List:
Edge List:
(0, 1)
(1, 2)
(1, 3)
(2, 3)
Weighted Edge List:
Edge List (Weighted):
(0, 1, 2) // Edge from vertex 0 to 1 with weight 2
(1, 2, 3) // Edge from vertex 1 to 2 with weight 3
(1, 3, 1) // Edge from vertex 1 to 3 with weight 1
(2, 3, 5) // Edge from vertex 2 to 3 with weight 5
Tabular Representation:
| Edge | Weight |
| 0-1 | 2 |
| 1-2 | 3 |
| 1-3 | 1 |
| 2-3 | 5 |
Use Cases:
Kruskal's Algorithm: Edge lists are very useful in algorithms like Kruskal's Algorithm for finding the Minimum Spanning Tree (MST), where sorting the edges by weight is required.
Edge-centric algorithms: Some algorithms focus on manipulating edges rather than vertices, making an edge list ideal.
Pros:
Space efficient: Especially for sparse graphs (where the number of edges is much smaller than the number of vertices squared), an edge list is compact and efficient.
Simple: It’s straightforward to implement and understand.
Cons:
Inefficient for dense graphs: For dense graphs with many edges, the adjacency matrix is often better since an edge list doesn’t allow for quick neighbor lookups.
Traversal inefficiency: Finding the neighbors of a vertex requires searching the entire list of edges.
4. Implicit Graph Representation
An Implicit Graph is a representation where the graph is not explicitly stored in memory using adjacency lists or matrices. Instead, the graph is conceptualized based on the problem context. This is often the case with grid-based problems or logical representations.
Example:
A classic example of an implicit graph is a 2D grid where each cell represents a vertex, and edges are implied based on movement between the cells.
For instance, in a grid, you can move up, down, left, or right from a cell, and each move represents an edge to a neighboring cell.
Example Grid:
0 1 2 3
----------
0| S . . E
1| # # . .
2| . . # .
3| . # . .
In this grid:
Vertices: Each cell
(i, j)represents a vertex.Edges: There are edges between adjacent cells (horizontally or vertically).
You can move:
- From
(0, 0)to(0, 1)or(1, 0), etc.
Movement in a 2D Grid:
For a cell
(i, j), you can move to:(i+1, j)(down)(i-1, j)(up)(i, j+1)(right)(i, j-1)(left)
Use Cases:
Pathfinding algorithms: Implicit graphs are often used in problems like maze solving, grid-based pathfinding, or game development, where the actual graph is not stored in memory, but the relationships between nodes (cells) are derived from the context.
Shortest Path Problems: Algorithms like BFS (Breadth-First Search) and DFS (Depth-First Search) can be used on grids without the need to explicitly store the edges.
Visualization:
You can think of a 2D matrix as a graph where:
Each cell is a vertex.
Each move to an adjacent cell represents an edge.
In the above example, starting at the S (start) and moving to the E (end) requires finding a path through the open cells (.), avoiding obstacles (#).
Pros:
Memory efficient: Since the graph is not explicitly stored, memory consumption is minimized.
Flexible: Works well for problems where edges and nodes are generated dynamically based on context.
Cons:
Hard to visualize: It can be challenging to reason about the graph without explicit storage.
Complex traversal: Requires careful handling of movement directions, boundaries, and obstacles.
Summary
Both Edge Lists and Implicit Graphs offer different approaches to graph representation, each suited for different kinds of problems.
Edge Lists are simple and efficient for sparse graphs or edge-centric algorithms but can be slow for dense graphs or when you need to frequently find neighbors.
Implicit Graphs are conceptual graphs where relationships are derived rather than stored. They are very useful in grid-based problems or dynamic scenarios like pathfinding but require careful implementation to manage movement and boundaries.
Each method has its place in graph theory and computer science, and choosing the right one depends on the specific problem you are trying to solve.
Conclusion on Graph Storage Methods
Each graph representation has its own strengths and weaknesses depending on the problem at hand:
Adjacency List is ideal for sparse graphs and is memory-efficient.
Adjacency Matrix offers fast edge lookups but is more memory-intensive.
Edge List is compact for storing edges but may not be ideal for traversal-heavy problems.
2D Matrix (or implicit graphs) is useful for grid-based or geometric problems.
Most of the time, Adjacency List is the go-to method for graph representation due to its balance between memory efficiency and traversal performance.
4. Applications of Graphs
Social networks: Represent relationships between users.
Search engines: Represent the web as a graph where pages are vertices and links are edges (PageRank algorithm).
Navigation systems: Use graphs to find the shortest paths (GPS, Google Maps).
Network routing: Routers use graphs to find the most efficient path for data packets.
Dependency graphs: Used in build systems (e.g., Maven, Gradle) to resolve dependencies.
Recommendation engines: Suggest items based on relationships between users and products (e.g., Amazon, Netflix).
Biology and Chemistry: Represent molecules as graphs where atoms are vertices and bonds are edges.
5. Creating a Graph (Adjacency List Implementation in Java)
To represent a graph in a program, we often use an adjacency list. This structure is efficient for representing sparse graphs, where most vertices are not connected to every other vertex. Here's how we can create a graph using an adjacency list in Java.
Step 1: Define the Structure of an Edge
First, let's talk about how we represent the edges in our graph. An edge connects two vertices and can also have a weight if the graph is weighted (as in our case).
In Java, we’ll define an Edge class. This class will have:
src(source): The starting vertex of the edge.dest(destination): The vertex where the edge ends.wt(weight): The weight of the edge (optional, but we are using it here).
Here’s how we create the class:
static class Edge {
int src; // Source vertex
int dest; // Destination vertex
int wt; // Weight of the edge
// Constructor to initialize an edge
public Edge(int s, int d, int w) {
this.src = s;
this.dest = d;
this.wt = w;
}
}
Explanation:
This class simply holds information about an edge. For example, if there's an edge between vertex 0 and vertex 1 with a weight of 5, we create an Edge object like this:
Edge e = new Edge(0, 1, 5);
Step 2: Create the Graph
To create the graph, we need to establish a way to represent all the vertices and their respective edges in a structured manner. We do this using an array of lists (or ArrayList in Java), where each index corresponds to a vertex in the graph, and each element at that index stores a list of edges that are connected to that vertex.
Why Use an Array of Lists?
Efficiency: An array of lists allows us to efficiently store and access the edges of each vertex. This is particularly useful for sparse graphs, where many vertices are not directly connected to each other.
Dynamic Sizing: Using ArrayLists lets us dynamically add edges without needing to predefine the number of edges connected to each vertex.
Step-by-Step Explanation
Define the Number of Vertices: We start by defining the number of vertices ( V ) in our graph. In our example, let’s assume we have 5 vertices. These vertices can be labeled from 0 to 4.
int V = 5; // Number of verticesCreate an Array of Lists: Next, we declare an array of
ArrayList<Edge>where the size of the array is equal to the number of vertices ( V ). This array will hold lists for each vertex. Each list will contain edges that represent connections to other vertices.ArrayList<Edge>[] graph = new ArrayList[V];At this point,
graphis an array that can hold references toArrayList<Edge>objects, but the individual lists are not yet initialized.Initialize Each List: Before we can use the array to store edges, we need to initialize each index of the array with a new
ArrayList<Edge>. This is done with a simple loop:for (int i = 0; i < V; i++) { graph[i] = new ArrayList<>(); // Initialize an empty list for each vertex }After this loop, each element of the
grapharray points to an empty list. For example:graph[0]will now point to an empty list representing edges for vertex 0.graph[1]will point to an empty list for vertex 1, and so on.
Visual Representation of the Structure
Here’s a visual representation of the graph structure after initialization:
graph[0] -> []
graph[1] -> []
graph[2] -> []
graph[3] -> []
graph[4] -> []
- Each
[]indicates an empty list, ready to store edges for the respective vertex.
Benefits of This Structure
Simplicity: The array makes it straightforward to access each vertex by its index.
Scalability: If we need to add more vertices, we can easily increase the size of the array (though it involves creating a new array and copying elements).
Dynamic Edge Storage: The
ArrayListat each index can grow dynamically as edges are added, making it suitable for graphs where the number of edges is not fixed.
Summary of Step 2
In this step, we have established the foundational structure of our graph using an array of ArrayList<Edge>. Each index corresponds to a vertex, and each list at that index will eventually hold edges representing connections to other vertices. This approach is both efficient and flexible, allowing for easy addition and retrieval of edges.
Step 3: Add Edges
Now that we have the structure set up, we can start adding edges to our graph. We do this by adding edges to the respective list of the source vertex.
In this step, we will add edges between vertices in our graph using the Edge class we defined earlier. Each edge consists of a source vertex, a destination vertex, and a weight that signifies the cost or distance between the two vertices.
Understanding the Edge Class
Before we dive into adding edges, let’s briefly recap the Edge class, which is used to represent an edge in the graph:
static class Edge {
int src; // Source vertex
int dest; // Destination vertex
int wt; // Weight of the edge
public Edge(int s, int d, int w) {
this.src = s;
this.dest = d;
this.wt = w;
}
}
Attributes:
src: The starting vertex of the edge.dest: The vertex that the edge points to (its destination).wt: The weight associated with the edge.
Adding Edges Step-by-Step
Vertex 0: For vertex 0, there is only one edge leading to vertex 1 with a weight of 5.
graph[0].add(new Edge(0, 1, 5)); // Edge from 0 to 1 with weight 5This means vertex 0 has a connection to vertex 1 with a weight of 5. After this addition, the adjacency list will look like this:
graph[0] -> [Edge(0, 1, 5)]Vertex 1: For vertex 1, there are three edges:
To vertex 0 with weight 5 (the reverse of the previous edge).
To vertex 2 with weight 1.
To vertex 3 with weight 3.
graph[1].add(new Edge(1, 0, 5)); // Edge from 1 to 0 with weight 5
graph[1].add(new Edge(1, 2, 1)); // Edge from 1 to 2 with weight 1
graph[1].add(new Edge(1, 3, 3)); // Edge from 1 to 3 with weight 3
After this addition, the adjacency list for vertex 1 will look like:
graph[1] -> [Edge(1, 0, 5), Edge(1, 2, 1), Edge(1, 3, 3)]
Vertex 2: For vertex 2, there are three edges:
To vertex 1 with weight 1.
To vertex 3 with weight 1.
To vertex 4 with weight 4.
graph[2].add(new Edge(2, 1, 1)); // Edge from 2 to 1 with weight 1
graph[2].add(new Edge(2, 3, 1)); // Edge from 2 to 3 with weight 1
graph[2].add(new Edge(2, 4, 4)); // Edge from 2 to 4 with weight 4
The adjacency list for vertex 2 becomes:
graph[2] -> [Edge(2, 1, 1), Edge(2, 3, 1), Edge(2, 4, 4)]
Vertex 3: For vertex 3, there are two edges:
To vertex 1 with weight 3.
To vertex 2 with weight 1.
graph[3].add(new Edge(3, 1, 3)); // Edge from 3 to 1 with weight 3
graph[3].add(new Edge(3, 2, 1)); // Edge from 3 to 2 with weight 1
The adjacency list for vertex 3 is:
graph[3] -> [Edge(3, 1, 3), Edge(3, 2, 1)]
Vertex 4: For vertex 4, there is only one edge leading to vertex 2 with a weight of 2.
graph[4].add(new Edge(4, 2, 2)); // Edge from 4 to 2 with weight 2The adjacency list for vertex 4 will look like this:
graph[4] -> [Edge(4, 2, 2)]
Final Adjacency List Representation
After adding all the edges, the complete adjacency list representation of the graph will be:
graph[0] -> [Edge(0, 1, 5)]
graph[1] -> [Edge(1, 0, 5), Edge(1, 2, 1), Edge(1, 3, 3)]
graph[2] -> [Edge(2, 1, 1), Edge(2, 3, 1), Edge(2, 4, 4)]
graph[3] -> [Edge(3, 1, 3), Edge(3, 2, 1)]
graph[4] -> [Edge(4, 2, 2)]
Understanding the Relationships
Bidirectional Edges: The edges from vertex 0 to vertex 1 and vice versa are symmetric, indicating that the connection between these vertices is bidirectional.
Weighted Connections: The weight of an edge can represent various real-world phenomena such as distance, time, cost, etc. For instance, the edge from vertex 1 to vertex 2 has a weight of 1, indicating a relatively short or low-cost connection.
Conclusion of Step 3
In this step, we effectively constructed the adjacency list by adding edges that represent the connections between the vertices. This representation is crucial for traversing the graph, performing algorithms like Dijkstra’s or Kruskal’s, and analyzing the structure of the graph.
Step 4: Accessing Neighboring Vertices
Once we've constructed the graph using an adjacency list, the next task is often to access and work with this data. Accessing elements from the adjacency list helps us retrieve information about the neighbors of a specific vertex or about the edges that connect two vertices.
Accessing Neighbors of a Vertex
Let's say we want to access all the neighbors of a particular vertex. The neighbors of a vertex are the vertices directly connected to it by edges. In our adjacency list, we store these edges in an ArrayList at each index corresponding to the vertex.
Example: Accessing the neighbors of vertex 2
To access the neighbors of vertex 2, we’ll loop through the ArrayList at index 2 of the graph. Each element in this list represents an edge originating from vertex 2, which will give us the connected vertices (neighbors).
Here’s how we do this in code:
// Accessing neighbors of vertex 2
for (int i = 0; i < graph[2].size(); i++) {
Edge e = graph[2].get(i); // Get the edge object from the adjacency list
System.out.println("Vertex 2 is connected to vertex: " + e.dest + " with a weight of: " + e.wt);
}
Explanation of the Code
Looping through the adjacency list:
- We use a loop that runs from
i = 0toi < graph[2].size()to iterate over all edges that start from vertex 2. This is becausegraph[2]contains all edges originating from vertex 2.
- We use a loop that runs from
Accessing the edges:
In each iteration of the loop, we retrieve an edge from the adjacency list using
graph[2].get(i). This gives us anEdgeobject, which contains:e.dest: The destination vertex that vertex 2 is connected to.e.wt: The weight of the edge between vertex 2 and the destination.
Printing the result:
- We print the destination vertex (
e.dest) and the weight (e.wt) of each edge that originates from vertex 2.
- We print the destination vertex (
Visualizing this Access
Let’s look at the edges originating from vertex 2 in the adjacency list:
graph[2] -> [Edge(2, 1, 1), Edge(2, 3, 1), Edge(2, 4, 4)]
The first edge connects vertex 2 to vertex 1 with a weight of 1.
The second edge connects vertex 2 to vertex 3 with a weight of 1.
The third edge connects vertex 2 to vertex 4 with a weight of 4.
So, when we run the loop, the output would be:
Vertex 2 is connected to vertex: 1 with a weight of: 1
Vertex 2 is connected to vertex: 3 with a weight of: 1
Vertex 2 is connected to vertex: 4 with a weight of: 4
Why Accessing Neighbors is Important
Accessing the neighbors of a vertex is fundamental for graph algorithms like:
Breadth-First Search (BFS): Where you visit all neighbors of a vertex before moving on to the next level of neighbors.
Depth-First Search (DFS): Where you explore one neighbor fully (and its neighbors) before exploring the next.
Shortest Path Algorithms: Like Dijkstra’s algorithm, where you need to access neighboring vertices and update their distances from a source vertex.
By efficiently accessing the neighbors, we can explore the graph, check for paths, find the shortest path, or even detect cycles.
Diagrammatic Representation of Access
Imagine the adjacency list like this:
graph[0] -> [Edge(0, 1, 5)]
graph[1] -> [Edge(1, 0, 5), Edge(1, 2, 1), Edge(1, 3, 3)]
graph[2] -> [Edge(2, 1, 1), Edge(2, 3, 1), Edge(2, 4, 4)]
graph[3] -> [Edge(3, 1, 3), Edge(3, 2, 1)]
graph[4] -> [Edge(4, 2, 2)]
When you access vertex 2:
You go to
graph[2], which contains[Edge(2, 1, 1), Edge(2, 3, 1), Edge(2, 4, 4)].From here, you extract each edge one by one and examine its destination (
dest) and weight (wt).
Conclusion
Accessing elements in the adjacency list is a fundamental part of working with graphs. By looping through the adjacency list for any vertex, we can retrieve all its neighbors and the respective edge weights. This is essential for exploring and manipulating the graph data structure in algorithms.
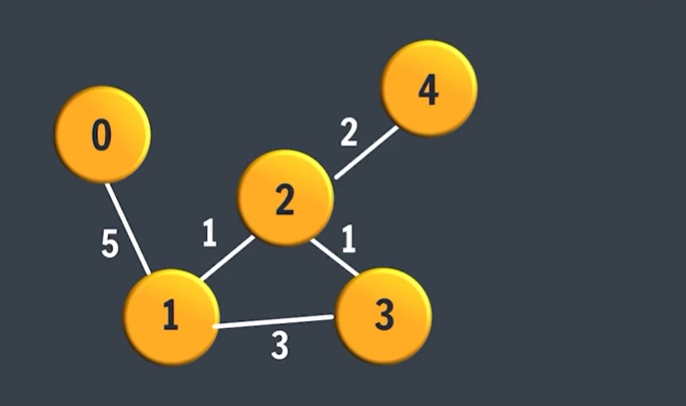
Step 5: Visual Representation of the Graph
Let’s look at a diagram of how the graph is structured based on the adjacency list:
(5)
0 -------- 1
/ \
(1) / \ (3)
2 ----- 3
| (1)
(2) |
|
4
Each vertex has a list of edges connecting it to its neighbors. For example:
Vertex 0 has one edge connecting it to vertex 1.
Vertex 1 has edges connecting it to vertices 0, 2, and 3.
And so on...
Step 6: Full Code
Here's the complete code that we just walked through:
import java.util.ArrayList;
public class Graph {
// Edge class to represent a graph edge
static class Edge {
int src; // Source vertex
int dest; // Destination vertex
int wt; // Weight of the edge
public Edge(int s, int d, int w) {
this.src = s;
this.dest = d;
this.wt = w;
}
}
public static void main(String[] args) {
int V = 5; // Number of vertices
// Create the graph (Array of ArrayLists)
ArrayList<Edge>[] graph = new ArrayList[V];
// Initialize each index with an empty list
for (int i = 0; i < V; i++) {
graph[i] = new ArrayList<>();
}
// Add edges based on the provided graph
// Vertex 0
graph[0].add(new Edge(0, 1, 5));
// Vertex 1
graph[1].add(new Edge(1, 0, 5));
graph[1].add(new Edge(1, 2, 1));
graph[1].add(new Edge(1, 3, 3));
// Vertex 2
graph[2].add(new Edge(2, 1, 1));
graph[2].add(new Edge(2, 3, 1));
graph[2].add(new Edge(2, 4, 2));
// Vertex 3
graph[3].add(new Edge(3, 1, 3));
graph[3].add(new Edge(3, 2, 1));
// Vertex 4
graph[4].add(new Edge(4, 2, 2));
// Print neighbors of vertex 2
System.out.println("Neighbors of vertex 2:");
for (int i = 0; i < graph[2].size(); i++) {
Edge e = graph[2].get(i);
System.out.println("Vertex 2 is connected to " + e.dest + " with weight " + e.wt);
}
}
}
Conclusion
To summarize:
We used an Edge class to represent each connection between vertices.
We created an array of lists to represent the adjacency list of the graph.
We added edges to the graph based on the given structure.
Finally, we accessed the neighbors of a vertex and printed the connections.
This adjacency list structure efficiently stores the graph and allows for easy retrieval of neighboring vertices.
6.Graph Traversal
In this section, we'll discuss Graph Traversal, a key concept when working with graphs. Just like in trees, where we have traversal techniques like preorder, inorder, and postorder, graphs also have their own traversal methods. The two most common traversal techniques are:
Breadth-First Search (BFS)
Depth-First Search (DFS)
However, unlike trees where we start traversal from the root node, graphs don’t have a natural root node. This means we can begin traversal from any vertex. Also, graphs might contain cycles, which can complicate traversal, so we need additional mechanisms to handle this.
Graph Traversal Types
1. Breadth-First Search (BFS)
BFS explores the graph layer by layer, starting from the source vertex and visiting all its immediate neighbors before moving to their neighbors. It’s similar to level order traversal in a tree, where each level is processed from left to right.
2. Depth-First Search (DFS)
DFS explores as far as possible along a branch before backtracking, just like preorder traversal in trees
6.1 Breadth-First Search (BFS)
Introduction to BFS
Breadth-First Search (BFS) is a graph traversal algorithm used to explore nodes in a graph systematically. The algorithm explores all nodes at the present depth level before moving on to nodes at the next depth level. BFS uses a queue to keep track of the nodes yet to be explored and a visited array to prevent revisiting nodes.
BFS is commonly used for:
Finding the shortest path in an unweighted graph.
Exploring all connected components of a graph.
Network broadcasting, where information spreads from one node to all others.
Key Concepts
Queue: The data structure used to maintain the order of node exploration.
Visited Array: A boolean array that tracks which nodes have been visited.
Adjacency List: A representation of the graph that stores nodes and their neighbors.
Graph Representation
Let’s use the following undirected graph:
1-------3
/ | \
/ | \
0 | 5
\ | / \
\ | / \
2------------4 6
Adjacency List of the Graph
The graph can be represented using an adjacency list:
| Vertex | Neighbors |
| 0 | 1, 2 |
| 1 | 0, 3 |
| 2 | 0, 4 |
| 3 | 1, 4, 5 |
| 4 | 2, 3, 5 |
| 5 | 3, 4, 6 |
| 6 | 5 |
How BFS Works (Step-by-Step Process)
Starting BFS from node 0, let’s go step by step through the process, tracking the queue, visited array, and current node at each stage.
3. BFS Execution with Detailed Visualization
Queue: This stores nodes to be processed in the order they were discovered.
Visited Array: This keeps track of the nodes that have already been visited.
Initial Setup
Queue:
[0](starting from node 0)Visited Array:
[False, False, False, False, False, False, False](no nodes visited yet)
| Step | Queue | Current Node | Neighbors Processed | Visited Array | Explanation |
| 1 | [0] | - | - | [False, False, False, False, False, False, False] | Start with the initial node (0) in the queue, and none are visited. |
| 2 | [1, 2] | 0 | 1, 2 | [True, False, False, False, False, False, False] | Node 0 is processed. Its neighbors 1 and 2 are added to the queue. Mark 0 as visited. |
| 3 | [2, 3] | 1 | 0, 3 | [True, True, False, False, False, False, False] | Node 1 is processed. Skip 0 (already visited) and add 3 to the queue. Mark 1 as visited. |
| 4 | [3, 4] | 2 | 0, 4 | [True, True, True, False, False, False, False] | Node 2 is processed. Skip 0 and add 4 to the queue. Mark 2 as visited. |
| 5 | [4, 5] | 3 | 1, 4, 5 | [True, True, True, True, False, False, False] | Node 3 is processed. Skip 1, 4 (visited/unvisited) and add 5. Mark 3 as visited. |
| 6 | [5] | 4 | 2, 3, 5 | [True, True, True, True, True, False, False] | Node 4 is processed. Skip 2, 3, and add 5. Mark 4 as visited. |
| 7 | [6] | 5 | 3, 4, 6 | [True, True, True, True, True, True, False] | Node 5 is processed. Add 6. Mark 5 as visited. |
| 8 | [] | 6 | 5 | [True, True, True, True, True, True, True] | Node 6 is processed, and BFS finishes. |
4. Visualizing the Visited Array with Boxes
At each step, the visited array will be visualized as boxes to show the status of each node.
Step-by-Step Visualization of the Visited Array
- Initial State (No nodes visited):
[ _0_ ] [ _1_ ] [ _2_ ] [ _3_ ] [ _4_ ] [ _5_ ] [ _6_ ]
[False] [False] [False] [False] [False] [False] [False]
- Step 1 (Visited
0):
[ 0 ] [ _1_ ] [ _2_ ] [ _3_ ] [ _4_ ] [ _5_ ] [ _6_ ]
[ True ] [False] [False] [False] [False] [False] [False]
- Step 2 (Visited
1and2):
[ 0 ] [ 1 ] [ 2 ] [ _3_ ] [ _4_ ] [ _5_ ] [ _6_ ]
[ True ] [ True ] [ True ] [False] [False] [False] [False]
- Step 3 (Visited
3):
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ _4_ ] [ _5_ ] [ _6_ ]
[ True ] [ True ] [ True ] [ True ] [False] [False] [False]
- Step 4 (Visited
4):
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ _5_ ] [ _6_ ]
[ True ] [ True ] [ True ] [ True ] [ True ] [False] [False]
- Step 5 (Visited
5):
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ _6_ ]
[ True ] [ True ] [ True ] [ True ] [ True ] [ True ] [False]
- Final State (All nodes visited):
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 6 ]
[ True ] [ True ] [ True ] [ True ] [ True ] [ True ] [ True ]
5. BFS Algorithm in Java
Here’s the implementation of BFS in Java, where we use an adjacency list and a queue to perform the traversal.
Code:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class BFS {
// Edge class representing an edge with source, destination, and weight
static class Edge {
int src;
int dest;
int wt;
public Edge(int s, int d, int w) {
this.src = s;
this.dest = d;
this.wt = w;
}
}
// Create the graph with adjacency lists
static void createGraph(ArrayList<Edge>[] graph) {
for (int i = 0; i < graph.length; i++) {
graph[i] = new ArrayList<>();
}
// Add edges to the graph (undirected graph)
graph[0].add(new Edge(0, 1, 1));
graph[0].add(new Edge(0, 2, 1));
graph[1].add(new Edge(1, 0, 1));
graph[1].add(new Edge(1, 3, 1));
graph[2].add(new Edge(2, 0, 1));
graph[2].add(new Edge(2, 4, 1));
graph[3].add(new Edge(3, 1, 1));
graph[3].add(new Edge(3, 4, 1));
graph[3].add(new Edge(3, 5, 1));
graph[4].add(new Edge(4, 2, 1));
graph[4].add(new Edge(4, 3, 1));
graph[4].add(new Edge(4, 5, 1));
graph[5].add(new Edge(5, 3, 1));
graph[5].add(new Edge(5, 4, 1));
graph[5].add(new Edge(5, 6, 1));
graph[6].add(new Edge(6, 5, 1));
}
// Perform BFS traversal and display output with levels
public static void bfs(ArrayList<Edge>[] graph) {
Queue<Integer> q = new LinkedList<>();
boolean[] vis = new boolean[graph.length];
int[] level = new int[graph.length]; // To keep track of levels
q.add(0); // Start from vertex 0
vis[0] = true;
System.out.println("Starting BFS Traversal from node 0:\n");
int currentLevel = 0;
System.out.println("Level " + currentLevel + ":");
while (!q.isEmpty()) {
int size = q.size(); // Number of nodes at the current level
for (int i = 0; i < size; i++) {
int curr = q.remove();
// Print visited node and its neighbors
System.out.print("Visited node: " + curr + " | Neighbors: ");
for (Edge e : graph[curr]) {
System.out.print(e.dest + " ");
if (!vis[e.dest]) {
vis[e.dest] = true;
q.add(e.dest);
level[e.dest] = level[curr] + 1;
}
}
System.out.println();
}
// Move to next level if the queue is not empty
if (!q.isEmpty()) {
currentLevel++;
System.out.println("------------------------");
System.out.println("Level " + currentLevel + ":");
}
}
System.out.println("\nBFS Traversal Completed.");
}
public static void main(String[] args) {
int V = 7; // Number of vertices in the graph
ArrayList<Edge>[] graph = new ArrayList[V];
createGraph(graph);
// Perform BFS traversal starting from node 0
bfs(graph);
}
}
Key Changes Made:
Tracking Levels:
- I introduced an array
level[]to track the BFS levels for each node. The level of the start node (node0) is initialized to0, and the levels of subsequent nodes are incremented based on their parent nodes in the BFS traversal.
- I introduced an array
Enhanced Output Format:
The BFS traversal now displays output level by level. Each level is printed with the corresponding nodes visited at that level and their neighbors.
After processing each level, the output includes a separator (
------------------------) before moving to the next level.
Processing Nodes by Level:
- The code now processes nodes in batches per level using a
forloop withsize = q.size(). This ensures that all nodes at a particular level are processed together before moving to the next level.
- The code now processes nodes in batches per level using a
Formatted Print Statements:
- For each node, the neighbors (edges) are printed alongside it for a clearer visualization of the graph's structure.
Sample Output:
Starting BFS Traversal from node 0:
Level 0:
Visited node: 0 | Neighbors: 1 2
------------------------
Level 1:
Visited node: 1 | Neighbors: 0 3
Visited node: 2 | Neighbors: 0 4
------------------------
Level 2:
Visited node: 3 | Neighbors: 1 4 5
Visited node: 4 | Neighbors: 2 3 5
------------------------
Level 3:
Visited node: 5 | Neighbors: 3 4 6
------------------------
Level 4:
Visited node: 6 | Neighbors: 5
BFS Traversal Completed.
Explanation of Output:
Level 0: The traversal starts from node
0, and its neighbors1and2are found.Level 1: Nodes
1and2are visited. Node1's neighbors are0and3, and node2's neighbors are0and4.Level 2: Nodes
3and4are visited. Node3's neighbors are1,4, and5. Node4's neighbors are2,3, and5.Level 3: Node
5is visited, and its neighbors are3,4, and6.Level 4: Node
6is visited, and its only neighbor is5.
At the end of the traversal, the message "BFS Traversal Completed" is displayed.
6.2 Depth-First Search (DFS)
Introduction to DFS
DFS is a depth-based traversal method that explores as far along a branch as possible before backtracking.DFS Pseudocode
Java Implementation:
public void dfs(int startVertex, Set<Integer> visited) { System.out.print(startVertex + " "); visited.add(startVertex); for (int neighbor : adjList.get(startVertex)) { if (!visited.contains(neighbor)) { dfs(neighbor, visited); } } }Example: Include diagrams showing the DFS path traversal process.
8. Has Path? (Using DFS)
Problem Statement
Determine whether there is a path between two nodes in a graph using DFS.Java Implementation:
public boolean hasPathDFS(int source, int destination, Set<Integer> visited) { if (source == destination) return true; visited.add(source); for (int neighbor : adjList.get(source)) { if (!visited.contains(neighbor)) { boolean hasPath = hasPathDFS(neighbor, destination, visited); if (hasPath) return true; } } return false; }Explanation with Visuals
Step-by-step guide with a real-world analogy, showing how paths between nodes can be traced using DFS.
Conclusion
Recap of key points: types of graphs, graph representations, BFS, DFS, and the "Has Path" problem.
Include appreciation, links to related blog posts, and further reading suggestions.
Subscribe to my newsletter
Read articles from Rohit Gawande directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
Rohit Gawande
Rohit Gawande
🚀 Tech Enthusiast | Full Stack Developer | System Design Explorer 💻 Passionate About Building Scalable Solutions and Sharing Knowledge Hi, I’m Rohit Gawande! 👋I am a Full Stack Java Developer with a deep interest in System Design, Data Structures & Algorithms, and building modern web applications. My goal is to empower developers with practical knowledge, best practices, and insights from real-world experiences. What I’m Currently Doing 🔹 Writing an in-depth System Design Series to help developers master complex design concepts.🔹 Sharing insights and projects from my journey in Full Stack Java Development, DSA in Java (Alpha Plus Course), and Full Stack Web Development.🔹 Exploring advanced Java concepts and modern web technologies. What You Can Expect Here ✨ Detailed technical blogs with examples, diagrams, and real-world use cases.✨ Practical guides on Java, System Design, and Full Stack Development.✨ Community-driven discussions to learn and grow together. Let’s Connect! 🌐 GitHub – Explore my projects and contributions.💼 LinkedIn – Connect for opportunities and collaborations.🏆 LeetCode – Check out my problem-solving journey. 💡 "Learning is a journey, not a destination. Let’s grow together!" Feel free to customize or add more based on your preferences! 😊