Mastering Stack Operations: From Basics to Advanced Algorithms in C++
 Alok Gupta
Alok Gupta
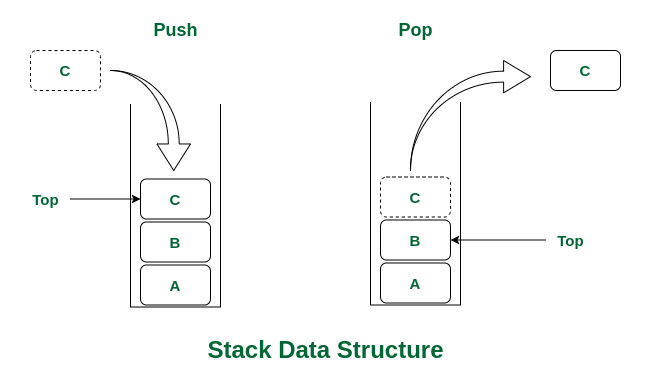
What is a Stack?
- Stack is a linear data structure that follows the LIFO (Last In First Out) or FILO (First In Last Out) principle. In a LIFO order, the element inserted last comes out first, and in FILO, the element inserted first is the last to be removed.
Basic Operations on Stack:
push(): Inserts an element into the stack.pop(): Removes the most recently added element from the stack.top(): Returns the top element of the stack.isEmpty(): Checks whether the stack is empty, returning true if it is, false otherwise.size(): Returns the number of elements present in the stack.
C++ Standard Template Library (STL) for Stack:
In C++, the
<stack>header file must be included to use stack functions.Basic stack functions in C++:
empty(): Returns whether the stack is empty in constant time, O(1).size(): Returns the size of the stack in constant time, O(1).top(): Returns the topmost element of the stack in constant time, O(1).complexity: O(1).push(g): Adds the element ‘g’ at the top of the stack – Time Complexity: O(1).pop(): Deletes the most recently entered element of the stack – Time Complexity: O(1).
C++ Example of Stack Operations:
#include <iostream> #include <stack> using namespace std; int main(){ stack<int> stack; stack.push(10); // Inserting element into the stack stack.push(20); // Inserting element into the stack stack.push(30); // Inserting element into the stack stack.push(40); // Inserting element into the stack int num = 0; stack.push(num); stack.pop(); // Removing elements from the stack stack.pop(); stack.pop(); while (!stack.empty()) { cout << stack.top() << " "; stack.pop(); } }Practice Questions:
Reversing a Stack
Coping stack into another stack in the same order
Display Stack elements
Reversing Stack Example:
#include<bits/stdc++.h> #include<stack> using namespace std; void display(stack <int> st){ while(st.size()>0){ cout<<st.top()<<" "; st.pop(); } cout<<endl; } int main(){ stack<int> st; stack<int> rt; stack<int> temp; st.push(8); st.push(18); st.push(28); st.push(38); st.push(48); st.push(58); display(st); while(st.size()>0){ //transferring from st to rt rt.push(st.top()); st.pop(); } // display(rt); while(rt.size() >0){ temp.push(rt.top()); rt.pop(); } // display(temp); while(temp.size()>0){ st.push(temp.top()); temp.pop(); } display(st); }Overflow and Underflow:
Stack Overflow: Occurs when trying to add an element beyond the stack's predefined capacity. In C++, this may lead to memory corruption or program crashes. This issue can be mitigated by using dynamic data structures or performing capacity checks.
Stack Underflow: Occurs when trying to pop an element from an empty stack. Handling this requires checking if the stack is empty before performing a pop operation.
Reversing a Stack Recursively:
void Reverse(stack<int>& St) { if (St.size() == 1) return; int curr = St.top(); St.pop(); Reverse(St); insert(St, curr); }Linked List vs. Vector Implementation of Stacks:
Array Implementation:
#include<iostream> using namespace std; class Stack{ //user defined data structure public: int arr[6]; int idx; Stack(){ idx = -1; } void push(int val){ if(idx== (sizeof(arr)/sizeof(arr[0])) -1){ cout<<"Stack OverFlow\n"; return; } idx++; arr[idx] = val; } void pop(){ if(idx<=-1){ cout<<"Stack UnderFlow\n"; return; } idx--; } int top(){ if(idx ==-1){ cout<<"Stack is empty\n"; return -1; } return arr[idx]; } void size(){ cout<<"Current Size of stack is: " <<idx+1<<endl; } void display(){ while((idx+1)>0){ cout<<top()<<" "; pop(); } cout<<endl; } }; int main(){ Stack st; st.pop(); st.top(); st.push(10); st.push(20); st.push(30); st.push(40); st.push(50); st.push(60); st.push(23); cout<<st.top()<<endl; // st.display(); st.pop(); st.size(); // st.display(); }Linked List Implementation:
#include<iostream> using namespace std; class Node{ public: int val; Node* next; Node(int val){ this->val = val; this->next = NULL; } }; class Stack{ public: Node* head; int size; Stack(){ size = 0; head = NULL; } void push(int val){ Node* temp = new Node(val); temp->next = head; head = temp; size++; } void pop(){ if(head == NULL){ cout<<"Empty Stack\n"; return; } Node* temp = head; head = head->next; delete temp; size--; } int top(){ if(head == NULL){ cout<<"Empty Stack\n"; return -1; } return head->val; } void print(Node* temp){ if(temp == NULL) return; print(temp->next); cout<<temp->val<<" "; } void display(){ Node* temp = head; print(temp); cout<<endl; } }; int main(){ Stack st; st.push(10); st.push(23); cout<<st.size<<endl; cout<<st.top()<<endl; st.display(); }Linked List Implementation Advantages:
Dynamic size without pre-allocated memory.
Efficient insertion and deletion.
No fixed capacity.
Linked List Implementation Disadvantages:
Extra memory overhead due to the need for linked list node pointers.
Slower random access.
Vector (Dynamic Array) Implementation Advantages:
Direct random access to elements using indexing.
Simple implementation.
Pre-allocation for better performance if the maximum size is known.
Vector Implementation Disadvantages:
Dynamic resizing may require reallocation, which is time-consuming.
Potential overflow if a fixed capacity is exceeded.
Some Problems on Stack:
Balanced Brackets Problem:
Example:
Input: exp = “[()]{}{[()()]()}” Output: Balanced Input: exp = “[(])” Output: Not Balanced
Code to Check for Balanced Brackets in C++:
bool isBalanced(string s){ int n = s.length(); if(n%2 != 0){ return false; } else{ if (s[0] == ')') return false; else{ stack<char> st; for(int i=0;i<n;i++){ if(s[i] == '(') st.push(s[i]); else { if(st.size() == 0) return false; else st.pop(); } } return true; } } }Next Greater Element (NGE) Problem:
For each element, find the first element greater than it to its right.
Example:
Input: arr[] = {4, 5, 2, 25} Output: 4 --> 5 5 --> 25 2 --> 25 25 --> -1Code:
```cpp #include using namespace std; int main(){ int arr[]={3,1,2,7,4,6,2,3}; int n = sizeof(arr)/sizeof(arr[0]); for(int i = 0;i<n;i++){ cout<<arr[i]<<" "; } cout<<endl;
// Using 2 nested loops to get next greater element // Brute Force:: TC: O(n^2); SC: O(1) // // int nge[n]; // for(int i =0;iarr[i]){ // nge[i] =arr[j]; // break; // } // } // }
// Using stack int nge[n]; stack st; nge[n-1] = -1; st.push(arr[n-1]); for(int i =n-2;i>=0;i--){ while(st.size()>0 && st.top()<=arr[i]){ st.pop(); } if(st.size()==0){ nge[i]=-1; } else nge[i] = st.top(); st.push(arr[i]); } for(int i = 0;i<n;i++){ cout<<nge[i]<<" "; } cout<<endl; }
4. **Stock Span Problem:**
* Input: `N = 7, price[] = {100, 80, 60, 70, 60, 75, 85}`
* Output: `1 1 1 2 1 4 6`
* Explanation: The span Si of the stock's price on a given day i is defined as the maximum number of consecutive days just before the day for which the price is less than or equal to the price on the current day.
5. **Sliding Window Maximum Problem (Leetcode 239):**
* Given an array `nums` and an integer `k`, return the maximum of each sliding window of size `k`.
* Example:
```cpp
Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
Output: [3,3,5,5,6,7]
Infix, Prefix, Postfix Expressions:
Infix, Prefix, and Postfix Expressions:
Infix Notation: Operators are placed between operands (e.g.,
A + B).Prefix Notation (Polish Notation): Operators are placed before operands (e.g.,
+ A B).Postfix Notation (Reverse Polish Notation): Operators are placed after operands (e.g.,
A B +).
Infix to Postfix Conversion:
Converting infix expressions to postfix.
Example:
#include<bits/stdc++.h> using namespace std; int prio(char ch){ if(ch == '+' || ch == '-'){ return 1; } else if (ch == '*' || ch == '/') { return 2; } return 0; // Return 0 for any other character } string work(string val1, char ch, string val2){ string s = ""; s+=val1; s+=val2; s.push_back(ch); return s; } int main(){ string s = "2+6*4/8-3"; stack<char>op; stack<string>val; for(int i =0;i<s.size();i++){ if(s[i] >= 48 && s[i] <= 57){ // If true, it is a digit val.push(to_string(s[i] - 48)); // Convert char to integer and push } else{ // If it's not a digit (it's an operator) if(op.size()==0 || (prio(op.top()) < prio(s[i]))){ op.push(s[i]); // If operator stack is empty, just push operator } else{ // While current operator precedence is less than or equal to top of stack while(!op.empty() && prio(op.top()) >= prio(s[i])){ char ch = op.top(); op.pop(); string val2 = val.top(); val.pop(); string val1 = val.top(); val.pop(); string ans = work(val1, ch, val2); val.push(ans); } op.push(s[i]); // Push the current operator } } } // Process remaining operators in the stack while(!op.empty()){ char ch = op.top(); op.pop(); string val2 = val.top(); val.pop(); string val1 = val.top(); val.pop(); string ans = work(val1, ch, val2);; val.push(ans); } // Output the final result cout << val.top() << endl; }
Postfix Evaluation:
Postfix expressions can be evaluated by scanning the expression left to right and using a stack to store operands.
Example:
#include<bits/stdc++.h> using namespace std; int solve(int val1, int val2, char ch){ if(ch == '+'){ return val1 + val2; }else if(ch == '-'){ return val1 - val2; }else if(ch == '*'){ return val1 * val2; }else if(ch == '/'){ return val1 / val2; }else return 0; } int main(){ string s = "79+4*8/3-"; stack<int>val; for(int i =0;i<s.size();i++){ if(s[i] >= 48 && s[i] <= 57){ // If true, it is a digit val.push(s[i] - 48); // Convert char to integer and push } else{ // If it's not a digit (it's an operator) // work(evaluation) int val2 = val.top(); val.pop(); int val1 = val.top(); val.pop(); int ans = solve(val1,val2,s[i]); val.push(ans); } } // Output the final result cout << val.top() << endl; // cout<<2+6*4/8-3<<endl; cout<<(7+9)*4/8-3<<endl; // cout<<7+9*4/8-3<<endl; }
Prefix to Postfix Conversion:
Prefix expressions are converted to postfix by first converting them to infix, then converting the infix expression to postfix.
Example:
#include<bits/stdc++.h> using namespace std; string solve(string val1, string val2, char ch){ // pre to postfix // v1 v2 op string s = ""; s+=val1; s+=val2; s.push_back(ch); return s; } int main(){ string s = "-/*+79483"; stack<string>val; for(int i =s.size()-1;i>=0;i--){ if(s[i] >= 48 && s[i] <= 57){ // If true, it is a digit val.push(to_string(s[i] - 48)); // Convert char to integer and push } else{ // If it's not a digit (it's an operator) // work(evaluation) string val1 = val.top(); val.pop(); string val2 = val.top(); val.pop(); string ans = solve(val1,val2,s[i]); val.push(ans); } } // Output the final result cout << val.top() << endl; // cout<<2+6*4/8-3<<endl; cout<<(7+9)*4/8-3<<endl; // cout<<7+9*4/8-3<<endl; }Conclusion:
In this comprehensive guide, we've delved deep into the world of stacks, a fundamental data structure that plays a critical role in problem-solving across various domains. We've covered everything from understanding the basics like push, pop, and peek operations to tackling more advanced concepts such as stack overflow, underflow, and converting infix expressions to postfix and prefix. Working in C++ stacks offer a powerful, versatile tool for efficiently managing data in a LIFO (Last In, First Out) order.
By exploring practical examples and algorithms, such as balanced bracket validation, the Next Greater Element problem, and the stock span challenge, you’ve gained hands-on experience in applying stacks to real-world problems. Additionally, learning to handle stack-specific challenges like overflow and underflow ensures that your applications are both efficient and robust.
With the foundational knowledge and advanced techniques outlined here, you're well-equipped to tackle a wide range of programming challenges, utilizing stacks to their fullest potential. Keep practicing and experimenting with different implementations, and soon enough, stacks will become an integral part of your coding toolkit!
Thank You!
Subscribe to my newsletter
Read articles from Alok Gupta directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Alok Gupta
Alok Gupta
I’m an aspiring web developer keen on learning new things. I’m dedicated to keeping up to date with the latest stuffs in web development. I always lookout for chances to grow and learn. When I’m not coding, I enjoy reading about India’s fascinating history. It helps satisfy my curiosity and teaches me about the diverse India.