Lovelace's Program: Part 8 - Going Beyond "human head & hands"
 Greg Alt
Greg Alt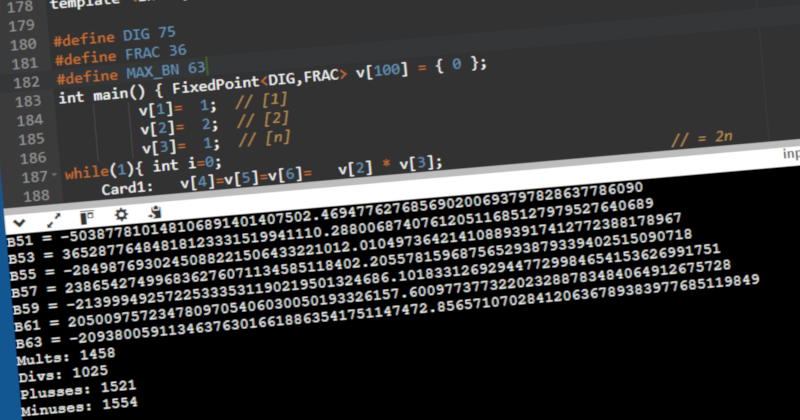
This is the eighth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program
My last post was the culmination of my efforts to get Ada Lovelace’s program to run on a modern computer.
My process started with the original published program as an image of the table in her Note G. I then transcribed this table to an essentially identical text table in a spreadsheet to allow more straightforward processing. I presented the python script I used to transliterate the table from .csv file to compilable C source code.
I then compiled and ran this resulting code, and found that it didn’t work as intended right away. After a fixing a couple bugs and extending the language of the table to support Lovelace’s intent of autoincrement addressing, I made a couple more efforts to compile and run. This succeeded in satisfying a few of Lovelace’s goals contained in her stated aim of "computing the Bernoulli Numbers to an indefinite extent, from the very beginning."
I was able to run and watch as each result was generated, B1, B3, B5, B7, and so on.
Few people writing about Lovelace’s program have gotten that far, and fewer still have commented on how far it can go before the results become meaningless due to overflow or exploding compounding errors. This progressively worse accuracy becomes clear if you have a list of the correct expected results to compare against.1
Looking at the results we see that by B33, everything to the right of the decimal point is wrong:
B1 = 0.166666666666666666671
B3 = -0.0333333333333333333315
B5 = 0.0238095238095238095032
B7 = -0.0333333333333333332096
B9 = 0.0757575757575757564801
B11 = -0.253113553113553098914
B13 = 1.16666666666666639721
B15 = -7.0921568627450915015
B17 = 54.9711779448619529131
B19 = -529.124242424234631166
B21 = 6192.12318840543233378
B23 = -86580.2531135327127458
B25 = 1425517.16666532310046
B27 = -27298231.0677131764824
B29 = 601580873.891570430715
B31 = -15116315766.1803309247
B33 = 429614642957.508138418
B1 is correct to 19 digits, B13 to 16 digits, B25 to 12 digits, and B33 is even worse at 8 digits correct, with every digit wrong to the right of the decimal point.
Continuing further, B59 is the right order of magnitude but only has 1 correct digit. B63 has no correct digits, and things become meaningless garbage beyond that.
How would this have measured up for Lovelace?
Going Beyond “human head & hands”
In Part 2 I pointed out that in choosing the problem to solve with her program, she wanted "an example of how an implicit function may be worked out by the engine, without having been worked out by human head & hands first."
At the time of Lovelace’s writing, the farthest anyone had gone by “head and hands” was a professor Rothe, who calculated and published B61 (by Lovelace’s numbering convention) in 1840. As B62 was known to be simply zero, to go beyond “head and hands” would require calculating B63 by machine.
This, B63, is the final goal of Lovelace’s that remains to be evaluated. Are the results of running her program accurate enough?
Before I can address that question, I need to be a bit more clear about what it means to store a number in a computer, whether Babbage’s Analytical Engine or a modern computer.
As it turns out, my modern transliteration to C uses an internal number format that is quite different than either Babbage or Lovelace were envisioning.
Floating Point vs Fixed Point
There are many different ways to store numbers in a computer. For this investigation, most of those distinctions don’t matter. The one distinction we care about is whether the decimal point is fixed in place for all values, known as fixed point, or whether the the decimal point can move based on the individual values, known as floating point.
As an example, to find the area of a pizza with radius 30cm, you use the formula, πr². Using 3.141592 as an approximation for π, you get 2827.433 cm², because 3.141592 × 30 × 30 = 2827.433.
That’s how we’d usually think about it and how we’d write it on paper, but it’s not how computers represent the values.
Floating Point
Another way to represent the calculation of the area of the pizza might be using scientific notation: 3.141592×10⁰ × 3.0×10¹ × 3.0×10¹ = 2.827433×10³
Each number has some string of digits, assumed to be one digit to the left of the decimal point, and then an exponent, that tells how much to float the decimal point to the left or right. Implementing the underlying math can be a bit complicated, but it has the advantage that you can accurately represent both very large numbers like the speed of light in meters per second, about 2.998×10⁸, but also very small numbers like the distance light travels in one second, about 3.336×10⁻⁹. These values are usually talked about in terms of the mantissa (2.998 and 3.336) and the exponent (8 and -9).
This way of storing numbers is called floating point because of the way each value can have the decimal point in a different place. On modern computers, the base of the exponent is generally 2, and the mantissa is stored in binary, but the concept is the same.
Fixed Point
Another way to store numbers is called fixed point. This is usually simpler to implement in hardware but has the downside that you need to pick a location for the decimal and all values need to be stored in terms of that. Using my pizza example above: 0.003141×10³ × 0.030000×10³ × 0.030000×10³ = 2.826900×10³
On the plus side, all numbers have the same exponent, so the hardware to do the math is simpler, especially for addition, which can just do straightforward integer math, ignoring the exponent.
On the down side, notice that we lost some digits of π and the result is a bit off as a result. Even worse, numbers larger than 9,999.999 can’t be stored at all, resulting in overflow failures.
Modern computers can use both, though floating point is more common due to it’s flexibility. In my transliterated C code in previous posts, I’ve used a type called “long double”. Compilers are free to implement it differently, but it often uses between 80 and 128 bits of memory. This can give up to about 33 decimal digits of precision.
Charles Babbage’s design of the Analytical Engine, on the other hand, used fixed point. Unlike modern computers, it was all base-10—each gear had 10 positions, from 0 to 9, and shifting by a power of 10 meant moving the gears up or down by the amount specified by the exponent. The precision could be expanded by extending the machine vertically, without otherwise fundamentally altering the design. For this reason, his initial description in 1837 specified 40 digits, and by 1864 he had expanded it to 50 stating, “It seems to me probable that a long period must elapse before the demands of science will exceed this limit.”2 In practice, if the machine had been built, the cost of the materials would have prevented unnecessarily large precision.
Lovelace’s notes were silent on the precise number of digits, so it’s not clear what her intended virtual machine supported. Either 40 or 50 digits would be a reasonable assumption.
Another important point is that Babbage’s design was such that the location of the decimal point could be chosen arbitrarily for a given run of a program. All variables and calculations would assume the same fixed decimal point location.
For example, if we assume 50 digits of precision, we might place the decimal point in the middle, with 25 digits to the left of the decimal point, and 25 digits to the right. Likewise, if we knew we’d be operating on particularly large values, we might give more digits to the left side to avoid overflow. For particularly small values, underflow, might be a concern, and the decimal point might be positioned to allow more digits to the right side to avoid very small values from being truncated to zero.
As it so happens, Bernoulli numbers grow very large, so this flexibility of setting the decimal point location is helpful in pushing Lovelace’s program to its limits.
I’m not the first to investigate the accuracy when running Lovelace’s program, but the only other attempt I’m aware of is in the EnigmaticCode blog. In their investigation, they ran with 50 digits of precision, 10 digits to the left of the decimal point, and 40 fractional digits to the right. As B33 requires 11 digits to the right of the decimal point, it would have overflowed. They calculated to B25:
B[25] = <+0001425517.1666666666666666666666666299288036638424>
And they documented the result of compounding error to that point:
“By the time we reach B[25] the last 15 digits of our 40 digits of decimal precision have been lost (B[25] = 8553103/6 = 1425517 + 1/6), but the computation is still correct to 25 decimal places.”
Adding Support for Fixed Point
For my investigation of the accuracy of Lovelace’s program, my first step was to replace the use of the floating point “long double” type with a suitable high-precision fixed point data type. I wanted a short and simple class that I could just paste in as a drop-in replacement. To achieve that, I adapted this BigInt class as a base implementation. This allowed arbitrary precision natural numbers using a simple base-10 string at it’s core. I removed parts I didn’t need and simplified the rest and then built a signed FixedPoint class on top of it. Note that my FixedPoint implementation is neither robust nor fast as short and simple were my priorities.
This class let me specify a number type with a fixed number of total digits of precision, and a fixed location of the decimal point. For example, FixedPoint<50,11> specifies 50 total digits, with 11 digits to the right of the decimal point.
Below is some code you can run to try it out yourself. To make it easier to do repeated runs without having to manually set breakpoints, I added some code at the end to print out the Bernoulli numbers and to exit when it reaches a target maximum. Otherwise, it’s just a simple drop-in replacement of the data type, with Lovelace’s program from my previous post untouched.
#include <bits/stdc++.h>
using namespace std;
// Class for arbitrary precision natural numbers, adapted from https://www.geeksforgeeks.org/bigint-big-integers-in-c-with-example/
class BigNat {
string digits;
public:
BigNat(unsigned long long n = 0) { do { digits.push_back(n % 10); } while (n /= 10); }
BigNat(const string &s) { for (int i = s.size() - 1; i >= 0; i--) digits.push_back(s[i] - '0'); }
void SetDigits(const string &s) { digits = s; }
int ToInt() {
string r(digits.rbegin(), digits.rend());
for(char& c : r) c+='0';
return std::stoi(r);
}
static BigNat PowerTen(int n) { return BigNat("1" + string(n, '0')); }
bool IsZero() const { return digits.size() == 1 && digits[0] == 0; }
int Length() const { return digits.size(); }
int operator[](const int index) const { return digits[index]; }
const string &ToString() const { return digits; }
BigNat &operator+=(const BigNat &b) {
int n = Length();
int m = b.Length();
if (m > n)
digits.append(m - n, 0);
n = max(n,m);
int carry = 0;
for (int i = 0; i < n; i++) {
int sum = digits[i] + carry + ((i < m) ? b.digits[i] : 0);
carry = sum / 10;
digits[i] = (sum % 10);
}
if (carry)
digits.push_back(carry);
return *this;
}
BigNat operator+(const BigNat &b) const { return BigNat(*this)+=b; }
BigNat &operator-=(const BigNat &b) {
int n = Length();
int m = b.Length();
for (int i = 0, borrow = 0; i < n; i++) {
int sum = digits[i] + borrow - ((i < m) ? b.digits[i] : 0);
borrow = (sum < 0) ? -1 : 0;
digits[i] = (sum < 0) ? sum + 10 : sum;
}
for (; n > 1 && digits[n - 1] == 0; n--)
digits.pop_back();
return *this;
}
BigNat operator-(const BigNat &b) const { return BigNat(*this)-=b; }
bool operator==(const BigNat &b) const { return digits == b.digits; }
bool operator<(const BigNat &b) const {
if (Length() != b.Length()) return Length() < b.Length();
return string(digits.rbegin(), digits.rend()) < string(b.ToString().rbegin(), b.ToString().rend());
}
bool operator<=(const BigNat &b) const { return !(*this > b); }
bool operator>(const BigNat &b) const { return b < *this; }
bool operator>=(const BigNat &b) const { return !(*this < b); }
BigNat &operator*=(const BigNat &b) {
if (IsZero() || b.IsZero()) return *this = BigNat();
int n = digits.size(), m = b.digits.size();
vector<int> accum(n + m, 0);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
accum[i + j] += (digits[i]) * (b.digits[j]);
n += m;
digits.resize(accum.size());
for (int i = 0, carry = 0; i < n; i++) {
int sum = carry + accum[i];
carry = sum / 10;
digits[i] = sum % 10;
}
for (int i = n - 1; i >= 1 && digits[i] == 0; i--)
digits.pop_back();
return *this;
}
BigNat operator*(const BigNat &b) const { return BigNat(*this) *= b; }
BigNat &operator/=(const BigNat &b) {
if (*this < b) return *this = BigNat();
else if (*this == b) return *this = BigNat(1);
int n = Length();
int m = b.Length();
BigNat t;
int i = n - 1;
for (; t * 10 + digits[i] < b; i--)
t = t * 10 + digits[i];
int lgcat = 0;
vector<int> cat(n, 0);
for (int cc; i >= 0; i--) {
t = t * 10 + digits[i];
for (cc = 9; b * cc > t; cc--) {}
t -= b * cc;
cat[lgcat++] = cc;
}
digits.resize(cat.size());
for (int i = 0; i < lgcat; i++)
digits[i] = cat[lgcat - i - 1];
digits.resize(lgcat);
return *this;
}
BigNat operator/(const BigNat &b) const { return BigNat(*this) /= b; }
friend ostream &operator<<(ostream &out, const BigNat &a);
};
ostream &operator<<(ostream &out, const BigNat &a) {
for (int i = a.digits.size() - 1; i >= 0; i--) out << (short)a.digits[i];
return out;
}
// Class for signed fixed point with digitcount total digits and fractional digits to the right of the decimal
template <int digitcount, int fractional> class FixedPoint {
static BigNat shiftx;
BigNat num;
bool neg = false;
FixedPoint &Clamp() {
num.SetDigits(num.ToString().substr(0, std::min(digitcount,num.Length())));
neg = neg && !num.IsZero();
return *this;
}
public:
static int mults, divs, plusses, minuses;
FixedPoint(const BigNat &num, bool neg) : num(num), neg(neg) {}
FixedPoint(const int n) : FixedPoint(BigNat(abs(n)) * shiftx, n < 0) {}
FixedPoint(const FixedPoint &a) : FixedPoint(a.num, a.neg) {}
FixedPoint() : FixedPoint(0) {}
int ToInt() { return (num / shiftx).ToInt() * (neg ? -1 : 1); }
FixedPoint &operator+=(const FixedPoint &b) {
plusses++;
if (neg == b.neg) num += b.num;
else if (num > b.num) num -= b.num;
else *this = FixedPoint(b.num - num, !neg);
return Clamp();
}
FixedPoint &operator-=(const FixedPoint &b) {
minuses++; plusses--;
*this += FixedPoint(b.num, !b.neg);
return Clamp();
}
FixedPoint operator+(const FixedPoint &b) const { return FixedPoint(*this) += b; }
FixedPoint operator-(const FixedPoint &b) const { return FixedPoint(*this) -= b; }
bool operator==(const FixedPoint &b) const { return num == b.num && neg == b.neg; }
bool operator>(const FixedPoint &b) const { return (neg != b.neg) ? !neg : (neg ? b.num > num : num > b.num); }
bool operator>=(const FixedPoint &b) const { return !(*this < b); }
bool operator<(const FixedPoint &b) const { return b > *this; }
bool operator<=(const FixedPoint &b) const { return b >= *this; }
FixedPoint &Helper(const BigNat &mul, const BigNat &div, bool bneg) {
*this = FixedPoint(num = num * mul / div, neg = neg != bneg);
return Clamp();
}
FixedPoint &operator*=(const FixedPoint &b) { mults++; return Helper(b.num, shiftx, b.neg); }
FixedPoint operator*(const FixedPoint &b) const { return FixedPoint(*this) *=b; }
FixedPoint &operator/=(const FixedPoint &b) { divs++; return Helper(shiftx, b.num, b.neg); }
FixedPoint operator/(const FixedPoint &b) const { return FixedPoint(*this) /= b; }
friend ostream &operator<<(ostream &o, const FixedPoint &a) {
string s = static_cast<std::ostringstream&>(std::ostringstream().seekp(0) << a.num).str();
int n = s.length() - fractional;
return o << (a.neg ? "-" : "") << (n <= 0 ? string("0") : s.substr(0, n)) << "."
<< (n <= 0 ? string(-n, '0') + s : s.substr(n));
}
};
template <int T, int F> BigNat FixedPoint<T,F>::shiftx(BigNat::PowerTen(F));
template <int T, int F> int FixedPoint<T,F>::mults = 0;
template <int T, int F> int FixedPoint<T,F>::divs = 0;
template <int T, int F> int FixedPoint<T,F>::plusses = 0;
template <int T, int F> int FixedPoint<T,F>::minuses = 0;
#define DIG 50
#define FRAC 40
#define MAX_BN 25
int main() { FixedPoint<DIG,FRAC> v[100] = { 0 };
v[1]= 1; // [1]
v[2]= 2; // [2]
v[3]= 1; // [n]
while(1){ int i=0;
Card1: v[4]=v[5]=v[6]= v[2] * v[3]; // = 2n
Card2: v[4]= v[4] - v[1]; // = 2n-1
Card3: v[5]= v[5] + v[1]; // = 2n+1
Card4: v[11]= v[4] / v[5]; v[5]=v[4]=0; // = (2n-1)/(2n+1)
Card5: v[11]= v[11] / v[2]; // = 1/2*(2n-1)/(2n+1)
Card6: v[13]= v[13] - v[11]; v[11]=0; // = -1/2*(2n-1)/(2n+1) = A0
Card7: v[10]= v[3] - v[1]; // = n-1 (=3)
if(v[10]==0) goto AfterRepetition0;
Card8: v[7]= v[2] + v[7]; // = 2+0 = 2
Card9: v[11]= v[6] / v[7]; // = 2n/2 = A1
Card10: v[12]= v[21+i] * v[11]; i++; // = B1*2n/2 = B1A1
Card11: v[13]= v[12] + v[13]; v[12]=0; // = -1/2*(2n-1)/(2n+1)+B1*2n/2
Card12: v[10]= v[10] - v[1]; // = n-2 (=2)
if(v[10]==0) goto AfterRepetition0;
Card13: v[6]= v[6] - v[1]; // = 2n-1
Card14: v[7]= v[1] + v[7]; // = 2+1 = 3
Card15: v[8]= v[6] / v[7]; // = (2n-1)/3
Card16: v[11]= v[8] * v[11]; v[8]=0; // = 2n/2*(2n-1)/3
Card17: v[6]= v[6] - v[1]; // = 2n-2
Card18: v[7]= v[1] + v[7]; // = 3+1 = 4
Card19: v[9]= v[6] / v[7]; // = (2n-2)/4
Card20: v[11]= v[9] * v[11]; v[9]=0; // = 2n/2*(2n-1)/3*(2n-2)/4 = A3
Card21: v[12]= v[21+i] * v[11]; i++; // = B3*2n/2*(2n-1)/3*(2n-2)/3 = B3A3
Card22: v[13]= v[12] + v[13]; v[12]=0; // = A0 + B1A1 + B3A3
Card23: v[10]= v[10] - v[1]; // = n-3 (=1)
if(v[10]>0) goto Card13;
AfterRepetition0:
Card24: v[21+i]= v[21+i] - v[13]; v[13]=0; i++; // = B7
Card25: v[3]= v[1] + v[3]; v[6]=v[7]=0; // = n+1 = 4+1 = 5; by a Variable-card. by a Variable card.
cout << "B" << (2 * v[3].ToInt() - 3) << " = " << v[v[3].ToInt() + 19] << "\n";
if(2 * v[3].ToInt() - 3 >= MAX_BN) break;
}
cout << "Mults: " << FixedPoint<DIG,FRAC>::mults << "\n";
cout << "Divs: " << FixedPoint<DIG,FRAC>::divs << "\n";
cout << "Plusses: " << FixedPoint<DIG,FRAC>::plusses << "\n";
cout << "Minuses: " << FixedPoint<DIG,FRAC>::minuses << "\n";
}
Running With Fixed Point
You can paste it into onlinegdb to run, this time without breakpoints. You'll see this result:
B1 = 0.1666666666666666666666666666666666666666
B3 = -0.0333333333333333333333333333333333333332
B5 = 0.0238095238095238095238095238095238095232
B7 = -0.0333333333333333333333333333333333333294
B9 = 0.0757575757575757575757575757575757575385
B11 = -0.2531135531135531135531135531135531130492
B13 = 1.1666666666666666666666666666666666573437
B15 = -7.0921568627450980392156862745098036946514
B17 = 54.9711779448621553884711779448621483513091
B19 = -529.1242424242424242424242424242421532786701
B21 = 6192.1231884057971014492753623188278955535467
B23 = -86580.2531135531135531135531135524041332740759
B25 = 1425517.1666666666666666666666666199450649892008
Mults: 223
Divs: 170
Plusses: 248
Minuses: 262
As a nice confirmation, using the same fixed point configuration of 50 total digits with 40 fractional, I get the same accuracy that enigmaticcode reported for B25.
The counts of arithmetic operations performed lets us estimate the total runtime. Babbage’s estimate was that additions and subtractions would each take one second while multiplication and division would take one minute.3
Using that estimate as a guide, we can see that the above calculation would have taken 223+170 + (248+262)/60 minutes or just under 7 hours.
Getting back to the goal, how well would this code work to compute B63?
Looking up the exact value on WolframAlpha, we can see that it is:
-106783830147866529886385444979142647942017 / 510
Which is this repeating decimal (the last 16 digits repeat):
-209380059113463784090951852900279701847.09215686274509803
In order to calculate this value without overflow, we need at least 39 digits to the left of the decimal point. With 50 total digits, that means we need fixed point with 11 fractional digits.
Adjusting the #defines accordingly, I get the following result:
B1 = 0.16666666666
B3 = -0.03333333332
B5 = 0.02380952375
B7 = -0.03333333295
B9 = 0.07575757213
B11 = -0.25311350408
B13 = 1.16666575967
B15 = -7.09213478674
B17 = 54.97049330273
B19 = -529.09788000137
B21 = 6190.88912031827
B23 = -86511.23198025227
B25 = 1420971.50776141064
B27 = -26950038.70127271784
B29 = 570887907.92284698320
B31 = -12031346694.22541596515
B33 = 78908047018.46351982050
B35 = 31061194360152.28985014688
B37 = -5889899674222220.88567660759
B39 = 988853444077364972.95379309064
B41 = -175055361076791406221.12326945512
B43 = 33679070797656613968806.29749238983
B45 = -7070020084701822821385228.80796579041
B47 = 1616431961695390159065419995.70459312019
B49 = -401280561350821174768466678063.23388220922
B51 = 107827114828616582173127535568472.86034803675
B53 = -31267948682637323400210171087835259.17228174095
B55 = 9757773698330236828333171943984200006.78450903223
B57 = -268541024079413902555767993980971989494.53306125612
B59 = 350520261639093388993351237975275372004.89362482828
B61 = -209422447129465692503316430568917882008.92109464254
B63 = 998649635835694385869196822390123093236.04462239212
Mults: 1458
Divs: 1025
Plusses: 1521
Minuses: 1554
B63 is far from the correct answer with none of the digits correct. The count of arithmetic operations can be trusted, though, and they give us 1458+1025 + (1521+1554)/60 minutes or about 42 hours.
OK, where did it start to go wrong? It starts out with 11 digits correct in B1, but B27 has only 1 digit correct, and everything after that just gets worse.
Accuracy vs Precision
Before digging in to this problem I wanted to clarify the distinction between accuracy and precision. In this context, we can explicitly set the precision we are going to calculate with. In the above example, it’s 50 digits. Precision will be a constant 50 digits regardless of error. Accuracy, on the other hand, refers to how close the values are to the correct values.
In the above results, the variable storing B27 might have 50 digits of precision, but only the first digit is correct. The rest are garbage. This means it has only 1 digit of accuracy.
How Accurate is Enough?
In evaluating Lovelace’s goal of calculating something beyond anything “worked out by human head & hands first” it’s clear that the more accuracy the better, and complete garbage results wouldn’t count. One digit of accuracy isn’t particularly useful but it is perhaps a solid objective point. Anything worse is at best a rough estimate of order of magnitude, or at worst a meaningless random number that any human might have scribbled down. Anything better than one digit is information not previously worked out, and the more digits the more useful it might be.
As one example, it turns out that NASA-JPL consider 16 digits of pi to be sufficient. In calculating the circumference of a circle with radius equal to the distance of the farthest human-made probe, Voyager 1, the error would only be about one centimeter.
This precision is what you get with modern double-precision floating point numbers, represented by 64 bits. For many modern computations, single-precision is enough. These values have about 6 or 7 digits of precision and take up only 32 bits.
For the purposes of evaluating success of Lovelace’s goal, I would consider calculating B63 with 1 digit of accuracy would barely meet the goal.
Calculating it with 6 digits would have been a practical result with useful accuracy. Calculating it with 16 digits or more would have been sufficient for practical matters, if not for mathematicians seeking the exact rational values.
How Do We Bridge the Gap?
OK, my first attempt to use Lovelace’s program to calculate B63 fell short. What are our options to improve accuracy?
There are a few different options worth considering:
Add more digits to the hardware. If 50 digits doesn’t work, maybe 60 or 100 will.
Babbage wrote about the possibility of double-precision operations. This would mean the Analytical Engine hardware would stay at 40 or 50 digits precision, but you could effectively get the accuracy from 80 or 100 digit precision at the expense of extra time.
As B1...B61 had already been published, the program could be adapted to take the exact value of these as inputs, minimizing the effect of compounding error.
Babbage's design included the ability to use double precision internally when performing a multiplication followed by division. Lovelace’s program always had these operations reversed, but perhaps rearranging some operations would allow using this feature of Babbage’s design.
I’ll look at each of these in turn, evaluating accuracy as possible.
1. Add More Digits in Hardware
This is the simplest for me to test out, but probably the least likely for Lovelace to try, because greater precision adds proportionately to the size and cost of the physical machine. The advantage is the program would work as intended with no modifications.
Trying with 39 digits to the left and varying amounts of fractional digits to the right of the decimal, I found the following accuracy:
up to 60 total digits: B63 has 0 digits accurate
61 total digits: B63 has 2 digits accurate
66 total digits: B63 has 7 digits accurate
75 total digits: B63 has 16 digits accurate
80 total digits: B63 has 21 digits accurate
100 total digits: B63 has 41 digits accurate
From this we can see that 61 total digits precision would be barely enough to satisfy Lovelace’s goal, while 66 digits would give enough accuracy to be of practical use, and 75 digits would likely be sufficient for all but the exactness required by mathematicians.
The good news is that even 75 is only a 50% increase and would be sufficient. It’s likely, though, that Lovelace would have focused on other, software-only options.
2. Double-Precision Operations in Software
Babbage wrote about the possibility of calculating with greater precision than the hardware at the expense of extra time:
it appears that whatever may be the number of digits the Analytical Engine is capable of holding, if it is required to make all the computations with k times that number of digits, then it can be executed by the same Engine, but in an amount of time equal to k2 times the former.
He gives the example of multiplying two numbers, each represented with a pair of variables:
a . 1050 + b and a′ . 1050 + b′
The result of multiplying these 100 digit values would be:
a a′ 10100 + (a b′ + a′ b) 1050 + b b′
This would require special handling for carrying, but Babbage was confident this was be straightforward.
I suspect this would have been a primary focus for Lovelace upon seeing compounding error limit the range of computation to only that which was already “worked out by human head & hands first.”
Her program wouldn’t fundamentally change, and all of the conditional logic would remain the same. With a 4x execution time penalty, the computation would have taken 168 hours, a solid week. The result, though, on an Analytical Engine with 50 digits of hardware precision, would have been calculating B63 with 41 digits of accuracy.
As long as the decimal point was adjusted to avoid overflow on the largest Bernoulli number, this strategy would allow compute many more values, if with diminishing accuracy. For example, using 33 fractional digits, this would allow calculating up to B89 with 5 digits of accuracy.
3. Calculating with B1..B61 Given as Input
Another, simpler option Lovelace might have considered is leaving the hardware as-is and even leaving the program largely the same.
Remember in my Part 6 post when I had yet gotten Lovelace’s program computing from B1, but it could calculate indefinitely starting from B5 as long as B1 and B3 were given as input values?
As exact values of B1..B62 had been published, it would have been straightforward to carefully set them as input values in a similar way, and then run with n starting at 32 instead of 3.
Assuming 50 total digits of hardware precision and 9 fractional digits, I was able to calculate B63 with a usable 8 digits accuracy, and also B65 with 6 digits. I could push just a bit further if I used 7 fractional digits, calculating B63, B65, and B67, all with 4 digits accurate.
4. Internal Double-Precision Multiplication/Divide
This is a fascinating one for further investigation. The idea here is that Babbage’s design of the Analytical Engine actually supported an internal 100 digits of precision if you structured your code just right. A multiplication of two 50 digit values followed by a division of a 50 digit value would actually keep 100 digits of precision for the result of the multiplication and use this as the input to the division. This potentially reduces one source of compounding error. Babbage explains:
In order to be somewhat in advance of the greatest number that may ever be required, I chose fifty places of figures as the standard for the Analytical Engine. The intention being that in such a machine two numbers, each of fifty places of figures, might be multiplied together and the resultant product of one hundred places might then be divided by another number of fifty places.
A close look at Lovelace’s program, though, reveals that Lovelace made no attempt to use this feature. It seems like it would be somewhat straightforward to adjust her program, though. Instead of operations 15 and 16 being:
v8 = v6 / v7
v11 = v8 * v11
They would be:
v11 = v6 * v11
v11 = v11 / v7
There would be similar adjustments in a few other places.
Simulating this with my FixedPoint class would be a bit more difficult, though, and it would require some manual changes to the transliterated C code to support internal double-precision when performing a multiplication/division pair of operations.
It would be very interesting if this was enough to make 50 digits of precision succeed for B63.
As I said, I haven’t explored this option, but I expect Babbage would have suggested it as a first thing to try. In fact, I suspect if Babbage were to write this program instead of Lovelace, he would have used his better knowledge of the internal workings to arrange things this way in the first place.
If they used this approach, rearranging math operations to minimize error, that might have spurred discussions amongst Lovelace, Babbage, and mathematician acquaintances. This could have set them down the path that led von Neumann to write his 1947 paper, “Numerical Inverting of Matrices of High Order,” widely seen as the birth of modern numerical analysis. Von Neumann’s paper was a result of thinking methodically about problems that arose in the first programs run on the first computers. If the Analytical Engine had been constructed in the 19th century, Babbage and Lovelace would have encountered these same problems a century earlier.
Summary
I started out this blog series with my First Look at the First Program. I wanted to understand Ada Lovelace’s 1843 program that was incomprehensible to me on first glance. In my career as a software engineer, I’ve found the best way to understand code is to run it in a debugger, and, if possible, to sit down and have a collaborative discussion with the engineer who wrote it.
With going on two centuries between us, I won’t be sitting down with Lovelace, but I have tried to get the next best thing—reading what she has written, both in her famous Notes and her available private letters. While getting her program running, I used her goals and intent as my guide.
It is a bit of a conundrum to talk about a program satisfying goals if the computer it was designed for was never built. All programs have bugs, and running your code for the first time always gives you new thoughts about how it could be improved. For this reason, I consider my investigation to be a bit speculative and subjective, even as I have tried to keep it concrete and objective. All programs require some modifications after they are first written. Sometimes those changes might be extensive rewrites, and sometimes they are more minor adjustments.
My intent has been to focus on the most minimal adjustments needed to satisfy Lovelace’s goals and intent as written in her own words.
As I’ve methodically walked through this process, I’ve shown that her program can be made to satisfy all of these goals with minimal adjustments:
"Compute the [Bernoulli] Numbers""to an indefinite extent": iterating to calculate Bn, Bn+1, etc. until you choose to halt the machine."from the very beginning": starting with B1."without having been worked out by human head & hands first": to at least B63.
In Part 5: a Better Second Run I showed how a transliteration of her program from her table to C source code could successfully calculate the Bernoulli number, B7. I had to fix a couple of bugs, and I had to modify it to use the auto-increment addressing she described in detail. This satisfies the first goal.
In Part 6: Computing the Bernoulli Numbers to an Indefinite Extent I got it computing Bernoulli numbers B5, B7, and so on, indefinitely. This satisfies the second goal.
In Part 7 - Computing the Bernoulli Numbers to an indefinite extent, from the very beginning I gave a corrected table and a python script to transliterate to runnable C code. This final version starts from B1, the beginning, and computes indefinitely. This satisfies the third goal.
Finally, in this post, I’ve identified a specific criteria for determining if her program was capable of calculating something that had not yet “been worked out by human head & hands first.” As all Bernoulli numbers up to B62 had been published by 1842, this goal requires calculating B63. Even one digit of accuracy would satisfy this goal, but 6 digits would be enough to be considered practical.
Using her program as-is, and without going beyond Babbage’s planned 50 digits of hardware precision, I showed that it is possible to calculate B63 to 8 digits of accuracy (and B65 with 6 digits) by giving the already-published B1..B61 as fully-accurate input values.
Further, I showed that using Babbage’s idea of software double-precision in software it would have been possible to achieve 41 bits of accuracy for B63. It could also continue all the way to B89 with 5 digits of accuracy. This would have required a straightforward transformation of her program, and would have incurred a 4x execution time penalty.
Either of these approaches is enough to consider the fourth and final goal satisfied.
Along the way I’ve appreciated getting a better understanding of her program and her thoughts around it and around programming in general. Researching this one program has, in turn, brought to my attention it’s place and Ada Lovelace’s place amongst other notable programmers and hardware designers from her time through to the birth of the computer revolution in the 1940s.
Seemingly simple questions like “what is a computer?” and “what is a program?” took on complex significance as I dug into the details of the work of my other heroes including Charles Babbage, Grace Hopper, and Alan Turing, among others.
In my next blog post, I’ll outline my reasoning for describing Ada Lovelace’s 1843 Note G table as the first computer program.
If you remember that Bernoulli numbers are all exact rational numbers, you can look at the results for numbers known to have 6 as the denominator: B1, B13, B25, B33, B37, and B63. The decimal expansion for all of these should result with the same infinitely repeating .16666… to the right of the decimal point. This makes it easy to spot the extent of compounding error at a glance.
Passages from the Life of a Philosopher by Charles Babbage
"Sixty additions or subtractions may be completed and printed in one minute. One multiplication of two numbers, each of fifty figures, in one minute. One division of a number having 100 places of figures by another of 50 in one minute." Passages from the Life of a Philosopher by Charles Babbage
Subscribe to my newsletter
Read articles from Greg Alt directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
