[7] Understanding Paging in Computer Systems

As we discussed in segmentation, we fixed the problem by dividing memory into variable-sized pieces. Unfortunately, this solution has its own issues. When you split space into variable-sized chunks, it can become fragmented, making allocation harder over time.

In this article, we will introduce more advanced topics to solve this problem by dividing space into fixed-sized pieces. We call this idea paging.

Instead of dividing a process's address space into variable-sized segments (like code, heap, stack), we split it into fixed-sized units called pages. We also treat physical memory as an array of fixed-sized slots called page frames, where each frame can hold one virtual-memory page.

To make this approach clearer, let's use a simple example. The next figure shows a small address space of only 64 bytes, divided into four 16-byte pages. This small size is just to make it easier to understand. Real address spaces are much larger.

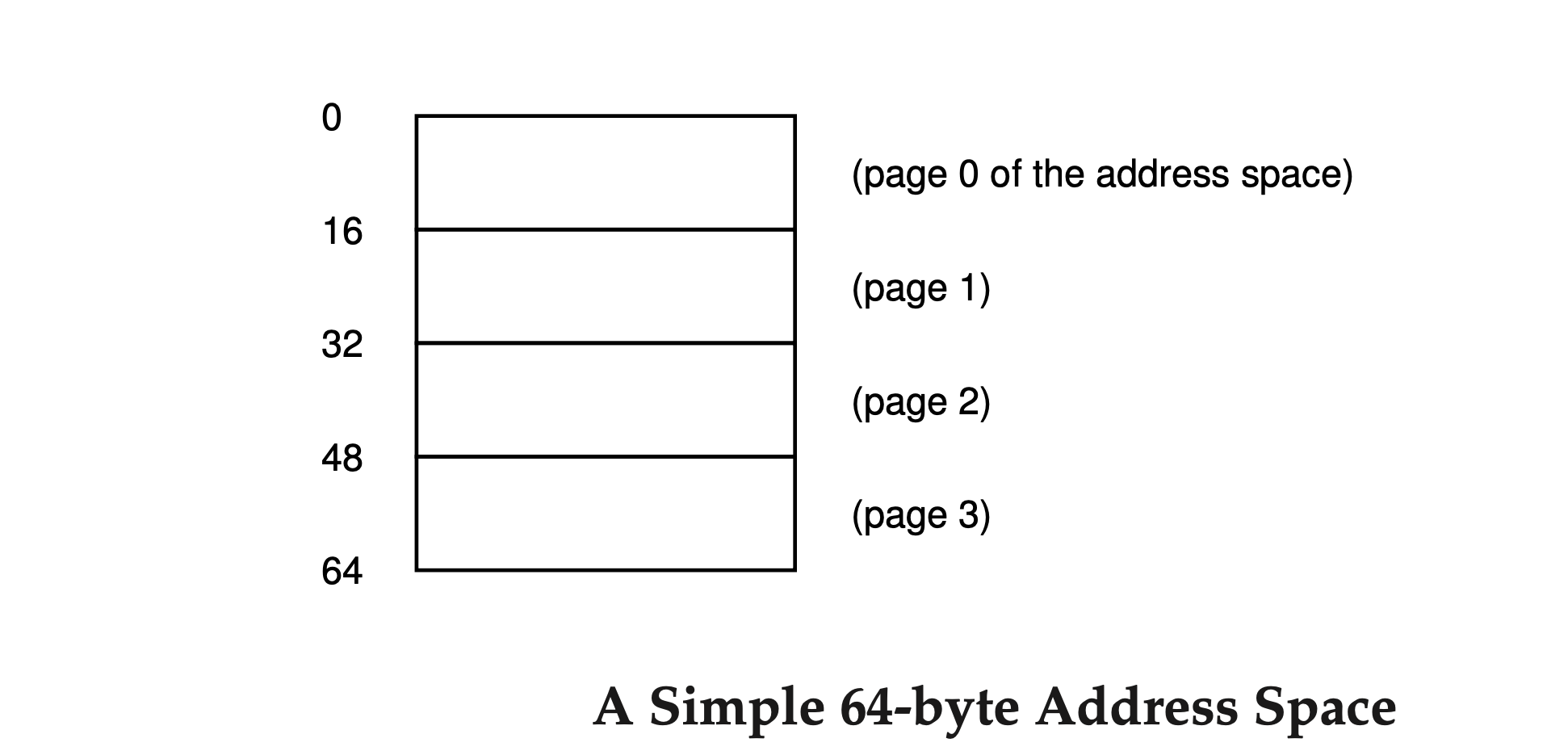
Physical memory also has a number of fixed-sized slots. In this case, there are eight page frames, making a 128-byte physical memory.

As you can see in the diagram, the pages of the virtual address space are placed at different locations in physical memory. The diagram also shows the OS using some of the physical memory for itself.

Paging offers several advantages over previous methods. One key benefit is the simplicity of free-space management. When the OS needs to place a 64-byte address space into the eight-page physical memory, it simply locates four free pages. The OS may maintain a free list of all available pages and selects the first four free pages from this list.

How can you find the specific page frame in physical memory for a particular virtual page?

To keep track of where each virtual page is placed in physical memory, the operating system uses a data structure called a page table for each process. The main job of the page table is to store the address translations for each virtual page, showing where each page is located in physical memory.

For our simple example above, the page table would have these four entries:

• (Virtual Page 0 → Physical Frame 3)

• (Virtual Page 1 → Physical Frame 7)

• (Virtual Page 2 → Physical Frame 5)

• (Virtual Page 3 → Physical Frame 2)

How to translate the virtual address to the physical address ?

To translate this virtual address, we have to first split it into two components: the virtual page number (VPN), and the offset within the page. For this example, because the virtual address space of the process is 64 bytes, we need 6 bits total for our virtual address( \(2^6= 46\) ). Thus, our virtual address can be conceptualized as follows:

The page size is 16 bytes in a 64-byte address space, so we need to select 4 pages (\(\frac{46}{16} = 4\)). The top 2 bits of the address do this. Therefore, we have a 2-bit virtual page number (VPN) (2² = 4). The remaining 4 bits tell us which byte of the page we are interested in; this is called the offset.

Example consider the following code:

movl 21, %eax

This code tries to load the data from address 21 into the register eax.

First turning “21” into binary form, we get “010101” and this is how it breaks down into a virtual page number (VPN) and offset:

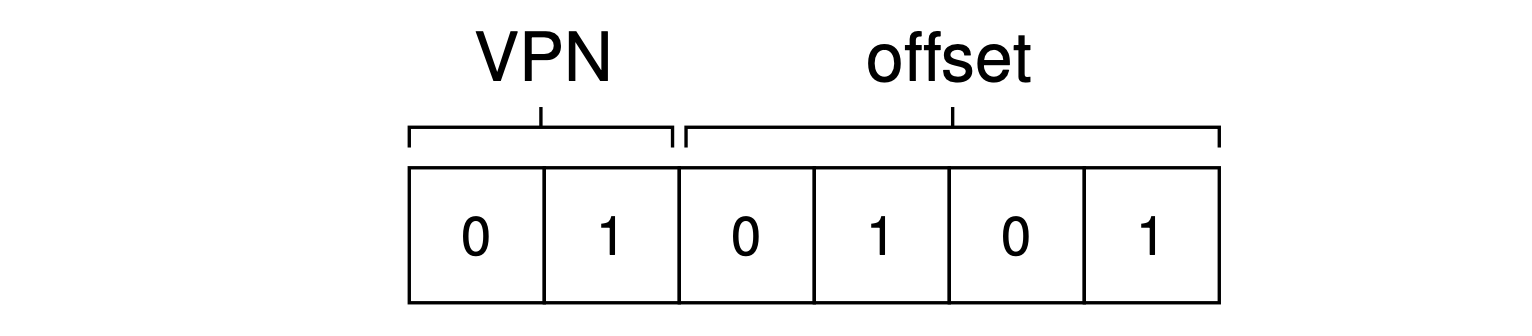
Thus, the virtual address “21” is on the 5th (“0101”th) byte of virtual page “01” (or 1).

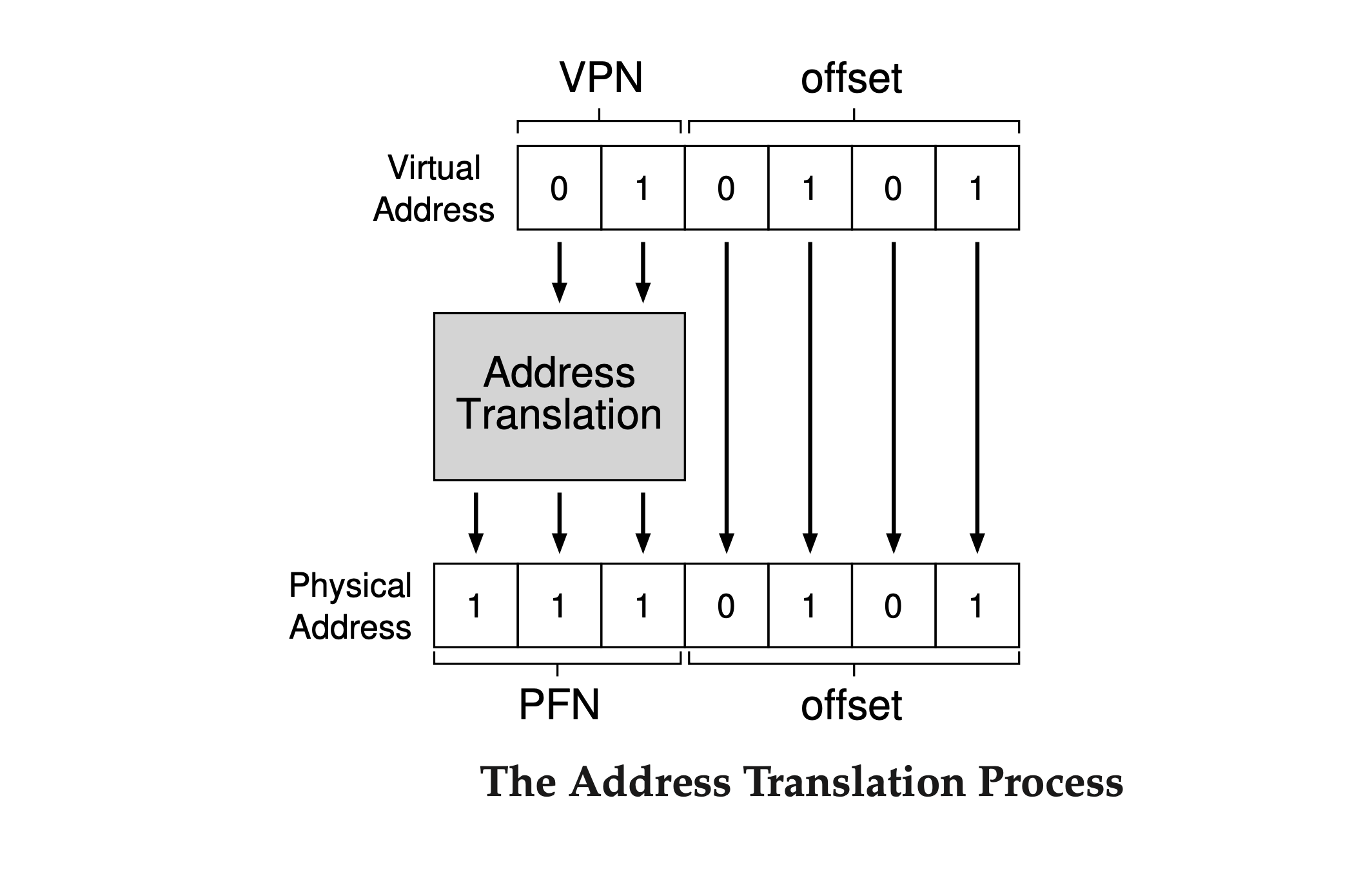
With our virtual page number, we can now look up our page table to find which physical frame virtual page 1 is in. In the page table above, the physical frame number (PFN) is 7 (binary 111). So, we can translate this virtual address by replacing the VPN with the PFN and then load the data from physical memory.

Note that the offset stays the same (it is not translated) because it just tells us which byte within the page we want. Our final physical address is 1110101 (117 in decimal), which is exactly where we want to fetch the data from.

With this basic overview in mind, we can now ask and answer some common questions about paging. For example, where are these page tables stored? What do they usually contain, and how big are they? Does paging slow down the system? These questions and more are addressed below. Read on!

---

In a system with a 32-bit address space and a 4KB page size, the virtual address is divided into a 20-bit virtual page number (VPN) and a 12-bit offset. A 20-bit VPN means the operating system must manage around one million translations (2^20), equivalent to 1MB of pages for each process.

If each page table entry (PTE) requires 4 bytes to store the physical address translation and other relevant data, the memory required for the page table would be 4MB per process.This is significant for multiple processes. With 100 processes running, the system would need 400MB of memory just for page tables.

Even though modern systems have gigabytes of memory, it seems a little crazy to use a large chunk of it just for translations, no?

Our first challenge is that the page table is quite large and consumes a lot of memory. For now, let's leave it as it is, and later we will understand how to solve this problem and answer our question about where this table is stored.

What’s Actually In The Page Table?

As we know The page table is a critical data structure that maps virtual addresses to physical addresses. Each entry in the page table, known as a page table entry (PTE), stores information to facilitate this translation

In an x86 PTE, several key bits control memory access and translation:

• Page Frame Number (PFN): Stores the actual physical frame where the page is located.

• Present Bit (P): Indicates whether the page is currently in physical memory or has been swapped to disk.

• Valid Bit: Determines if the page translation is valid. Pages marked invalid are not accessible, often representing unused memory.

• Protection Bits : Control access permissions.

  • Read/Write (R/W): Controls whether the page can be written to or is read-only.

  • User/Supervisor (U/S): Determines whether the page is accessible by user-mode processes or restricted to the OS.

• Accessed (A) and Dirty (D) Bits: Track whether the page has been accessed or modified, helping in page replacement decisions.

• Dirty (D) Bit: Indicates if the page has been modified since it was loaded into memory, signaling the need to write the page back to disk if it’s swapped out.

Other bits control caching behavior (PWT, PCD, PAT, G), but the core idea is that the PTE not only translates addresses but also enforces permissions and optimizes memory management.

Accessing Memory With Paging concept

Let's Take a simple memory access example to demonstrate all the resulting memory accesses that occur when using paging. See the following code snippet:

int array[1000];
...
for (i = 0; i < 1000; i++)
    array[i] = 0;

To really understand what memory accesses this code snippet will make, we need to disassemble it to see what assembly instructions are used to initialize the array in a loop. Here is the resulting assembly code:

1024 movl $0x0,(%edi,%eax,4)
1028 incl %eax
1032 cmpl $0x03e8,%eax
1036 jne 0x1024

The first instruction moves zero ($0x0) into the array's virtual memory address. This address is calculated by adding %edi (the base address of the array) and %eax (the index ‘i’ ) multiplied by 4, since each integer in the array is 4 bytes in size.

The second instruction increments the array index in %eax. The third instruction compares %eax to 0x03e8 (1000 in decimal). If they are not equal, the fourth instruction jumps back to the start of the loop.

Before we move on, we need to make some assumptions about where the code, array, and page table are located in physical memory.

Let's first assume we have virtual address space of size 64KB with a page size of 1KB.

• Page table

  Assume we have a linear (array-based) page table and that it is located at physical address 1KB (1024). There are just a few virtual pages we need to worry

  about having mapped

• Code

  There is a virtual page where the code lives. Assume it lives on the second virtual page and it's mapped to the fifth physical frame (VPN 1 → PFN 4).

• Array

  The array size is 4000 bytes (1000 integers), and we assume it resides at virtual addresses 40000 through 44000 (not including the last byte). The virtual pages for this range are VPN=39 to VPN=42. So, we need mappings for these pages. Let’s assume these virtual-to-physical mappings for the example: (VPN 39 → PFN 7), (VPN 40 → PFN 8), (VPN 41 → PFN 9), (VPN 42 → PFN 10).

Now we are ready to go, but keep in mind that when the program runs, each instruction fetch will generate two memory references:

One to the page table to find the physical frame where the instruction resides, and one to the instruction itself to fetch it to the CPU for processing.

Additionally, during a mov operation, there are two more memory accesses: one to the page table to translate the array's virtual address to the correct physical address, and another to access the array itself.

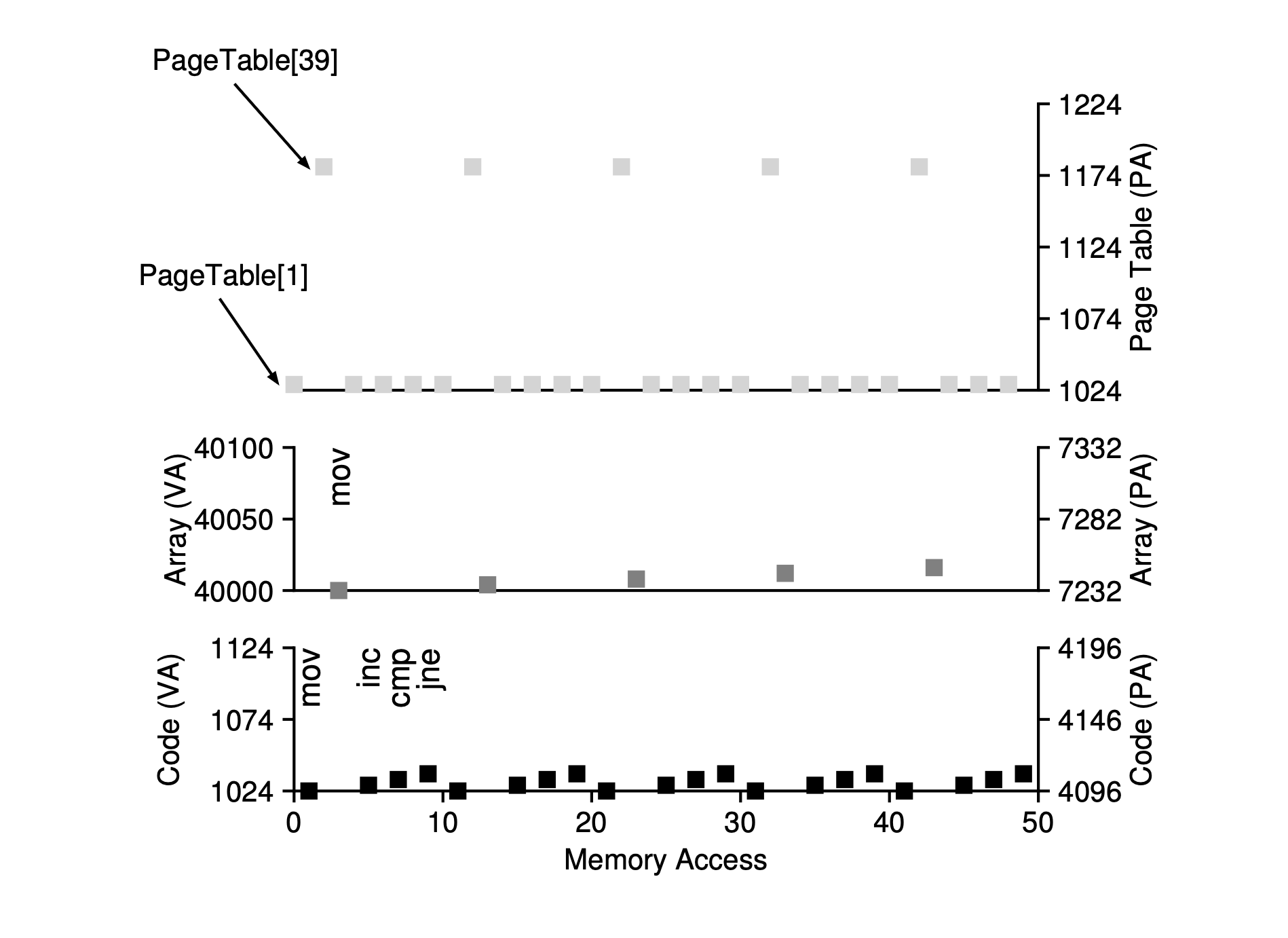
The figure shows the memory accesses for the first five loop iterations.

The bottom graph shows the instruction memory references on the y-axis in black (virtual addresses on the left and physical addresses on the right). The middle graph shows array accesses in dark gray (virtual on the left and physical on the right). The top graph shows page table memory accesses in light gray (just physical, as the page table is in physical memory). The x-axis shows memory accesses for the first five loop iterations. There are 10 memory accesses per loop: four instruction fetches, one memory update, and five page table accesses to translate those fetches and the update.

Now you can see that we have two main problems to solve. Without careful design of both hardware and software, page tables will make the system run too slowly and result in a slower machine as well as memory waste (with memory filled with page tables instead of useful application data). While page tables seem like a great solution for our memory virtualization needs, we need to carefully design a paging system that not only works but works efficiently.

Faster Translation

As we saw, paging logically requires an extra memory lookup for each virtual address generated by the program. Going to memory for translation information before every instruction fetch or explicit load or store is prohibitively slow. So, how can we speed up address translation and generally avoid the extra memory reference that paging seems to require? What hardware support is required? What OS involvement is needed?

Introducing translation-lookaside buffer (TLB).

To speed address translation, The OS usually needs help from hardware. we add a translation-lookaside buffer (TLB). A TLB is part of the chip's memory-management unit (MMU) and acts as a hardware cache for frequently used virtual-to-physical address translations. When there's a virtual memory access, the hardware first checks the TLB to see if it has the needed translation. If it does, the translation happens quickly without needing to check the page table. TLBs have a huge impact on performance and are essential for making virtual memory work effectively.

Consider the following code snippet to see how the OS translates a virtual address using a TLB.

1 VPN = (VirtualAddress & VPN_MASK) >> SHIFT
2 (Success, TlbEntry) = TLB_Lookup(VPN)
3 if (Success == True)  // TLB Hit
4     if (CanAccess(TlbEntry.ProtectBits) == True)
5         Offset = VirtualAddress & OFFSET_MASK
6         PhysAddr = (TlbEntry.PFN << SHIFT) | Offset
7         Register = AccessMemory(PhysAddr)
8     else
9         RaiseException(PROTECTION_FAULT)
10 else                 // TLB Miss
11     PTEAddr = PTBR + (VPN * sizeof(PTE))
12     PTE = AccessMemory(PTEAddr)
13     if (PTE.Valid == False)
14         RaiseException(SEGMENTATION_FAULT)
15     else if (CanAccess(PTE.ProtectBits) == False)
16         RaiseException(PROTECTION_FAULT)
17     else
18         TLB_Insert(VPN, PTE.PFN, PTE.ProtectBits)
19         RetryInstruction()

Here's how the hardware algorithm works: it gets the virtual page number (VPN) from the virtual address (Line 1) and checks the TLB for a translation (Line 2). If found, it's a TLB hit. We then get the page frame number (PFN), combine it with the offset, create the physical address, and access memory (Lines 5–7), if protection checks pass (Line 4).

If the CPU doesn't find the translation in the TLB (a TLB miss), it checks the page table for the translation (Lines 11–12). If valid and accessible (Lines 13, 15), it updates the TLB (Line 18). This process is costly due to extra memory access (Line 12). Once updated, the hardware retries the instruction, and memory access is fast.

The TLB, like all caches, relies on finding translations in the cache (hits) for quick access. When there's a miss, it becomes costly as the page table must be checked, leading to extra memory access. Frequent misses slow down the program since memory access is more expensive than CPU instructions. Thus, we aim to avoid TLB misses as much as we can.

Accessing Memory with TLB concept.

Caching is a basic way to improve performance in computer systems, used repeatedly to make common tasks faster. Hardware caches work by using the idea of locality in instruction and data references. There are usually two types of locality:

• Temporal locality:

  Recently accessed instructions or data are likely to be accessed again soon. such as loop variables or instructions in a loop, accessed repeatedly over time.

• Spatial locality:

  If a program accesses memory at address x, it will likely soon access memory near x. like streaming through an array, accessing one element and then the next.

Now let’s examine a simple virtual address trace for accessing an array and see how a TLB can improve its performance.

Assume we have an array of 10 4-byte integers in memory, starting at virtual address 100. We have an 8-bit virtual address space with 16-byte pages. This means a virtual address has a 4-bit VPN (16 virtual pages) and a 4-bit offset (16 bytes per page).

As you can see, Next figure shows the array laid out on the 16 16-byte pages of the system.

The array’s first entry (a[0]) starts at (VPN=06, offset=04); only three 4-byte integers fit on that page. The array continues on the next page (VPN=07) with entries (a[3]... a[6]). The last three entries (a[7]... a[9]) are on the following page (VPN=08).

Now, consider a simple loop in C that accesses each array element:

int sum = 0;
for (i = 0; i < 10; i++) {
    sum += a[i];
}

For simplicity, we'll assume the loop only accesses the array, ignoring the variables i and sum, and the instructions itself.

When the CPU accesses the first array element (a[0]), the virtual address points to VPN = 06. This triggers a TLB miss since it’s the first access. For the next element (a[1]), there’s a TLB hit because a[1] resides on the same virtual page as a[0]. The same occurs for a[2]. However, when accessing a[3], a TLB miss occurs, but subsequent elements (a[4] to a[6]) hit again due to spatial locality. Access to a[7] causes another miss, but a[8] and a[9] hit again. Overall, 7 out of 10 accesses result in TLB hits, giving a 70% hit rate. This illustrates how the TLB leverages spatial locality, where array elements close in memory are packed into the same page, minimizing the number of TLB misses. If the page size were larger, fewer misses would occur, and repeated access could further boost performance through temporal locality.

You might be wondering: if caches (like the TLB) are so great, why don’t we just make bigger caches and keep all of our data in them? Unfortunately, for a cache to be fast, it must be small due to physical limits like the speed of light. Large caches are slow and miss the point. So, we must figure out how to best use small, fast caches to boost performance.

Handling The TLB Miss

In the past, hardware had complex instruction sets (CISC), and hardware builders didn't trust OS developers much. So, the hardware managed the TLB miss completely. To achieve this, the hardware must know the location of the page tables in memory, using a page-table base register, used in Line 11 in the last snippet code.

Modern architectures often use a software-managed TLB. On a TLB miss, the hardware raises an exception, pausing the current instruction and switching to kernel mode. It then jumps to a trap handler, which is OS code designed to handle TLB misses. This code looks up the translation in the page table, updates the TLB using special instructions, and returns from the trap, allowing the hardware to retry the instruction, resulting in a TLB hit.

1 VPN = (VirtualAddress & VPN_MASK) >> SHIFT
2 (Success, TlbEntry) = TLB_Lookup(VPN)
3 if (Success == True)  // TLB Hit
4     if (CanAccess(TlbEntry.ProtectBits) == True)
5         Offset = VirtualAddress & OFFSET_MASK
6         PhysAddr = (TlbEntry.PFN << SHIFT) | Offset
7         Register = AccessMemory(PhysAddr)
8     else
9         RaiseException(PROTECTION_FAULT)
10 else                 // TLB Miss
11     RaiseException(TLB_MISS)

The return-from-trap instruction should differ slightly from the one used for a system call. It should continue at the instruction right after the trap into the OS, similar to how returning from a procedure call goes to the next instruction.

Context switches

With our basic understanding, we now know that the TLB entry should store the VPN and PFN to assist with successful translation for virtual-to-physical mappings. it can also contains some other bits like protection bits, valid and dirty bits.

To understand a context switch, consider this example: When process P1 runs, it expects the TLB to have its page table translations. Suppose P1's 10th virtual page maps to physical frame 100. Now, if process P2 is about to run, and its 10th virtual page maps to frame 170, the TLB would contain:

In the TLB above, there's a problem: VPN 10 translates to either PFN 100 (P1) or PFN 170 (P2), but the hardware can't tell which entry is for which process. We need to ensure the TLB supports virtualization efficiently across multiple processes.

There are several ways to solve this problem. One way is to clear the TLB during context switches, which empties it before the next process runs.

By emptying the TLB on each context switch, we now have a working solution, as a process will never accidentally encounter the wrong translations in the TLB. However, there is a cost: each time a process runs, it must incur TLB misses. If the OS switches between processes frequently, this cost may be high.

To reduce this overhead, we can simply add an address space identifier (ASID) field in the TLB to differentiate between entries with the same VPN.

Thus, with address-space identifiers, the TLB can hold translations from different processes at the same time without any confusion.

Another case that might occur is when two entries have the same PFN. This means two different processes have different VPNs that point to the same physical page:

This can happen when two processes share a page, like a code page. For example, Process 1 shares physical page 101 with Process 2. Process 1 maps it to the 10th page, while Process 2 maps it to the 50th page. Sharing code pages, like in programs or libraries, helps reduce memory use by lowering the number of physical pages needed.

Replacement Policy

As with any cache, including the TLB, we need to consider cache replacement. Specifically, when adding a new entry to the TLB, we must replace an old one. So, the question is: which one should we replace?

We will explore these policies in more detail in the next few articles.

A Real TLB Entry

Let's take a quick look at a real TLB. This example is from the MIPS R4000 , a modern system that uses software-managed TLBs. A simplified version of a MIPS TLB entry is shown in Figure.

The MIPS R4000 uses a 32-bit address space with 4KB pages. Normally, you'd expect a 20-bit VPN and a 12-bit offset in a virtual address. However, the TLB only uses 19 bits for the VPN because user addresses come from just half of the address space (the other half is for the kernel). So, only 19 bits for the VPN are needed. The VPN converts to a 24-bit physical frame number (PFN), allowing support for systems with up to 64GB of physical memory (\(2^{24}\) 4KB pages).

There are a few other interesting bits in the MIPS TLB.

• Global bit (G):

  Used for pages shared among processes. When set, the ASID (Address Space Identifier) is ignored.

• ASID:

  8-bit identifier used by the OS to differentiate between address spaces. Limits the system to 256 processes (as the ASID can hold 8 bits).

• Coherence bits (C):

  Three bits to determine how the page is cached by the hardware.

• Dirty bit (D):

  Set when the page has been written to, indicating it’s modified.

• Valid bit (V):

  Indicates whether there is a valid translation in the entry.

• Page mask (not shown):

  Supports multiple page sizes.

• Unused bits:

  Some bits are shaded gray in the diagram, indicating they are unused.

So far, We have seen how hardware can help us make address translation faster. By providing a small, dedicated on-chip TLB as an address-translation cache, most memory references will hopefully be handled without having to access the page table in main memory.

Building Smaller Page Tables

Now, let's tackle the second problem that paging introduces: page tables are too large and use too much memory.

Let's start with a linear page table. As you might remember, linear page tables can become quite large. Imagine a 32-bit address space with 4KB pages and a 4-byte page-table entry. This setup results in about one million virtual pages (\(\frac{2^{32}}{ 2^{12}}\)), making the page table 4MB in size.

Remember, we usually have around a hundred active processes, which is common in modern systems, we end up using hundreds of megabytes just for page tables. Therefore, we need techniques to reduce this heavy load.

Using Bigger Page Size.

As you might have considered, our goal is to reduce the size of the page table. The page table essentially contains a translation for each virtual page number to a physical frame number. Therefore, one approach is to decrease the number of pages by increasing the page size itself, which in turn reduces the number of page table entries.

Let's look at our 32-bit address space again, but now with 16KB pages. This gives us an 18-bit VPN and a 14-bit offset. With each PTE still being 4 bytes, we now have\(2^{18}\)entries in our linear page table, making the total size 1MB per page table.

Disadvantages of Bigger Page Size

The main problem with using large pages is that it leads to waste within each page, called internal fragmentation. Applications end up using only small parts of each page, and memory fills up with these large pages. So, most systems prefer smaller page sizes, like 4KB. Unfortunately, this won't solve our problem easily.

Using Hybrid : Paging and Segments

Whenever you have two reasonable but different approaches to something in life, you should always examine the combination of the two to see if you can obtain the best of both worlds. We call such a combination a hybrid.

Why not combine paging and segmentation to reduce the memory overhead of page tables? We can understand how this might work by taking a closer look at a typical linear page table.

Assume we have an address space in which the used portions of the heap and stack are small. For the example, we use a tiny 16KB address space with 1KB pages.

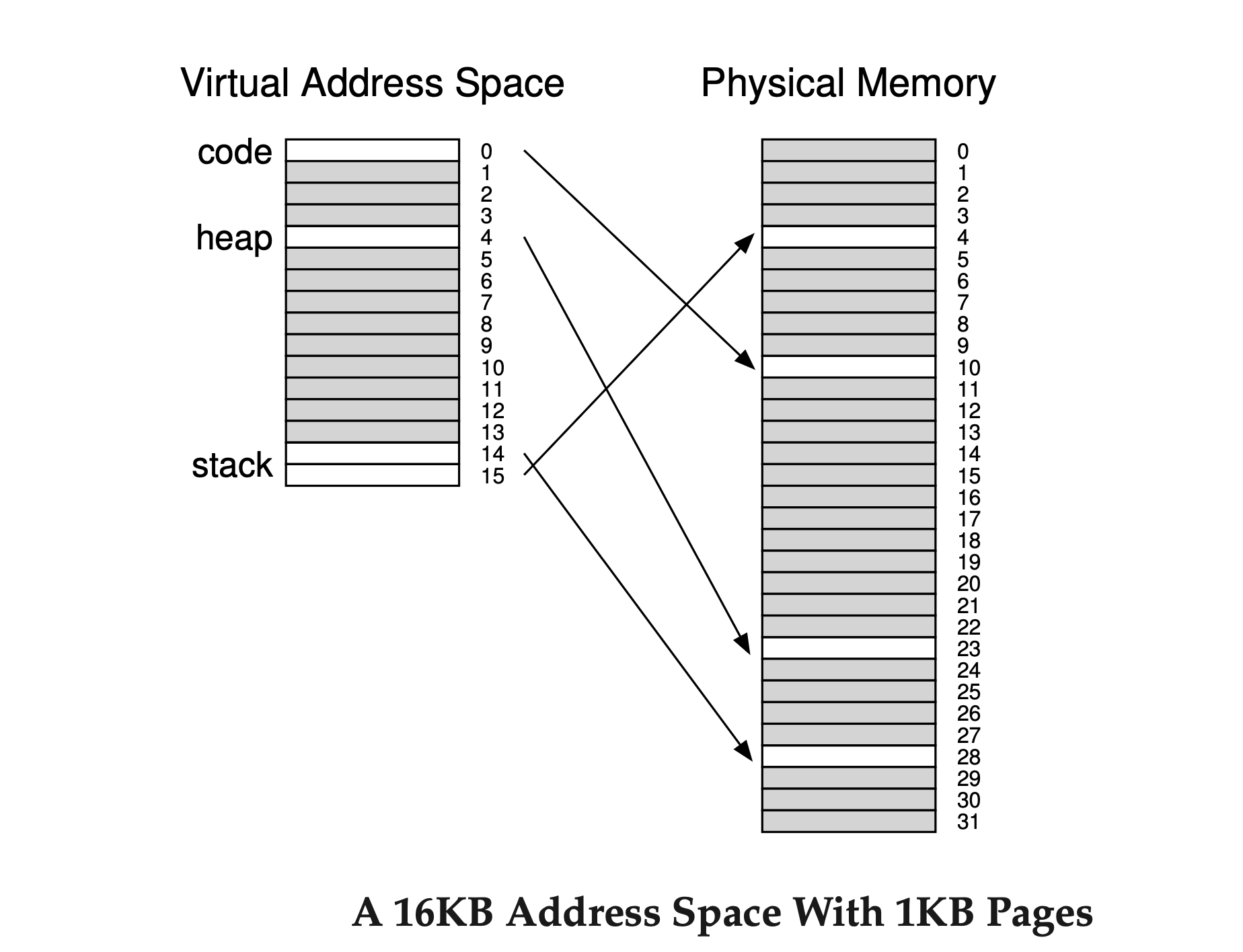
The page table for this address space is:

This example assumes the single code page (VPN 0) is mapped to physical page 10, the single heap page (VPN 4) to physical page 23, and the two stack pages (VPNs 14 and 15) to physical pages 28 and 4. Most of the page table is unused, full of invalid entries. This is wasteful even for a small 16KB address space. Imagine the waste in a 32-bit address space!

Thus, our hybrid approach: instead of one page table for the entire address space, why not have one for each logical segment? In this example, we have three page tables: one for the code, one for the heap, and one for the stack.

Now, remember with segmentation, we had a base and bound or limit register to. In our hybrid approach, we still have these structures in the MMU. Here, we use the base to hold the physical address of the page table for that segment instead of pointing to the segment itself. The bounds register shows the end of the page table.

Let's use a simple example. Assume a 32-bit virtual address space with 4KB pages, divided into four segments. For this example, we'll use three segments: one for code, one for the heap, and one for the stack.

To find out which segment an address belongs to, we'll use the top two bits of the address space. Let's assume 00 is the unused segment, 01 is for code, 10 is for the heap, and 11 is for the stack. So, a virtual address looks like this:

In the hardware, assume that there are thus three base/bounds pairs, one each for code, heap, and stack. When a process is running, the base register for each of these segments contains the physical address of a linear page table for that segment; thus, each process in the system now has three page tables associated with it. On a context switch, these registers must be changed to reflect the location of the page tables of the newly running process.

To form the address of the page table entry (PTE), The hardware takes the physical address therein and combines it with the VPN as follows:

SN = (VirtualAddress & SEG_MASK) >> SN_SHIFT
VPN = (VirtualAddress & VPN_MASK) >> VPN_SHIFT
AddressOfPTE = Base[SN] + (VPN * sizeof(PTE))

In our hybrid scheme, each bounds register keeps the value of the highest valid page in the segment. For instance, if the code segment uses its first three pages (0, 1, and 2), the code segment page table will have only three entries, and the bounds register will be set to 3.

Disadvantages of Hybrid approach

In this way, our hybrid approach saves a lot of memory compared to a linear page table. Unused pages between the stack and heap don't take up space in a page table just to show they're not valid.

However, this method has some issues. First, it still uses segmentation, which isn't as flexible as we'd like because it assumes a certain way the address space is used. For example, if we have a large but rarely-used heap, we can still waste a lot of page table space. Second, this hybrid approach brings back external fragmentation. Even though most memory is managed in page-sized units, page tables can now be any size (in multiples of PTEs), making it harder to find free space for them in memory. Because of these reasons, We need to keep searching for better ways to make smaller page tables.

Using A Multi-level Page Tables

A multi-level page table is an efficient way to manage large address spaces in operating systems by optimizing memory usage. Unlike a traditional linear page table, which allocates memory for all possible pages (even unused or invalid ones), the multi-level approach breaks the page table into smaller page-sized chunks. If an entire chunk contains invalid entries, it isn’t allocated, saving memory. This is achieved using a page directory, which tracks which parts of the page table are valid and where they are stored in memory.

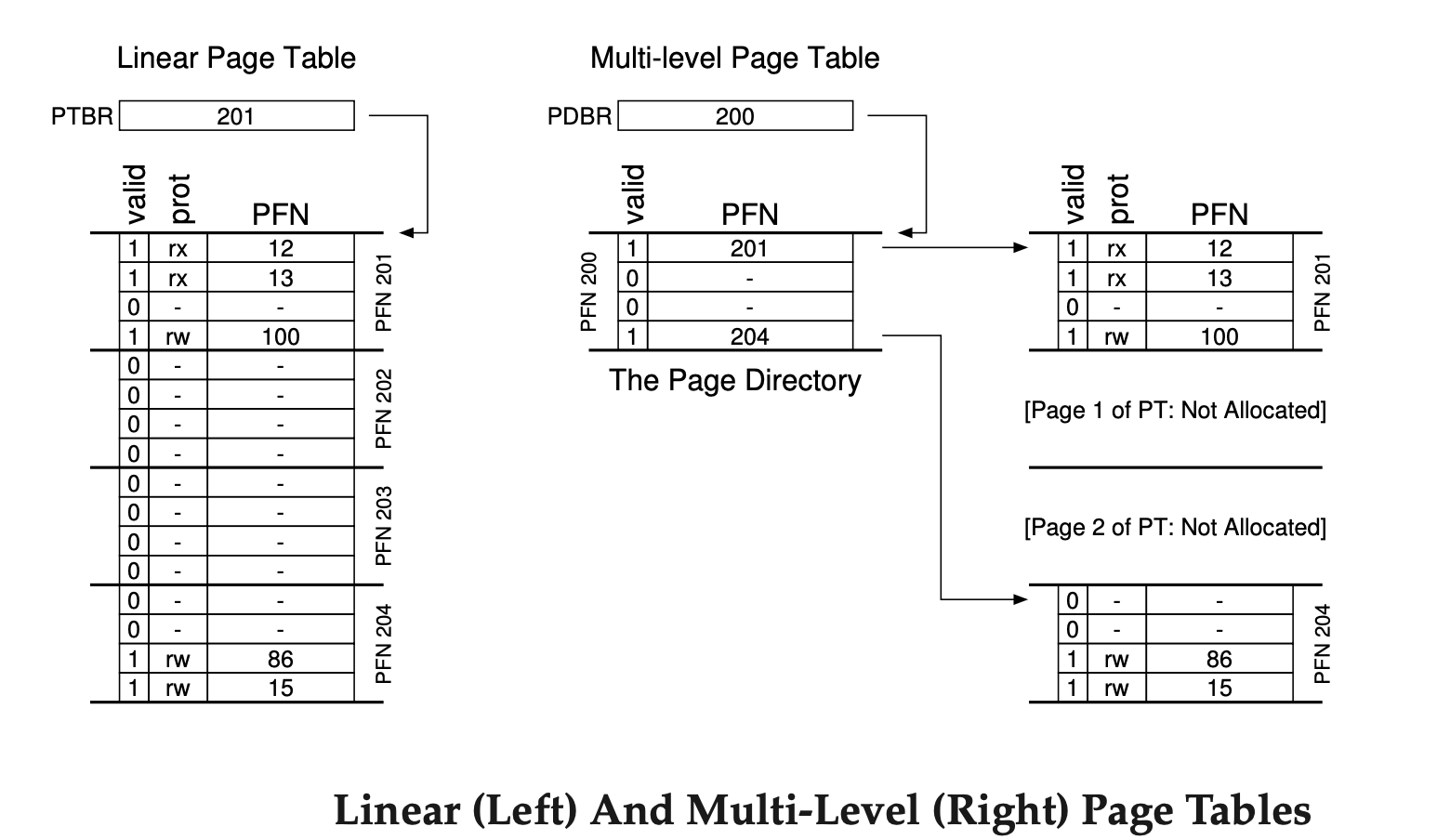
Each entry in the page directory (PDE) contains a valid bit and a Page Frame Number (PFN). If valid, the PDE points to a page of the page table containing at least one valid page table entry (PTE); if not, no memory is allocated for that page, avoiding waste. This structure is particularly useful for sparse address spaces, where large portions of memory are unused, and ensures that only the necessary parts of the address space are mapped.

Disadvantages of Multi-Level Page Tables

However, multi-level page tables come with a trade-off. On a TLB miss, they require two memory loads—one to access the page directory and another to retrieve the PTE—while a linear page table needs only one. This adds a slight performance cost, but the memory savings generally outweigh the slowdown. The multi-level table is also more complex to manage, but this complexity is a worthwhile trade-off for the efficiency gained in memory usage, making it an ideal solution for modern systems handling large, sparse address spaces.