Leetcode Explanation

Efficiently Solving Leetcode 240: Search A 2D Matrix II

Introduction:

In this article, I'll walk you through the thought process and solution for Leetcode problem 240: "Search a 2D Matrix II". This problem tests our ability to search in a 2D matrix with sorted rows and columns. I'll explain why direct binary search might fail and how we can optimize the search to achieve O(m + n) time complexity.

Problem Description:

We are given an m x n matrix where:

• Each row is sorted in ascending order from left to right.

• Each column is sorted in ascending order from top to bottom.
  The goal is to determine whether a target integer exists in the matrix.

Problem:

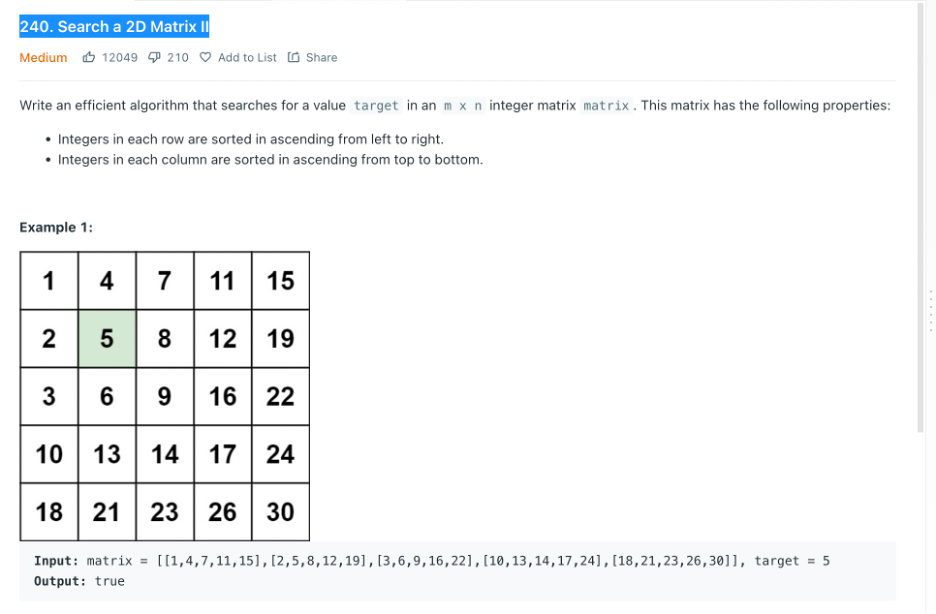
My Findings:

At first, applying a binary search on the matrix might seem intuitive. However, a direct binary search could fail because the target might be in a different row, and due to the sorting in columns, we might incorrectly exclude it.
To address this, we can start searching from the bottom-left corner of the matrix, where we can efficiently eliminate either a row or a column in each step.

Optimized Approach:

• Start from the bottom-left corner of the matrix.

• If the current element is greater than the target, move up (eliminate a row).

• If the current element is less than the target, move right (eliminate a column).

• Repeat until the target is found or we move out of bounds.

Pro Tip: Think about where we can start eliminating the rows. Start bottom row elimination and move above row until you find the target and return true, else false.

Code Presentation:

class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
N, M = len(matrix), len(matrix[0])
r, c = N - 1, 0 # Starting at the bottom-left corner

while r >= 0 and c < M:
if matrix[r][c] == target: # Finding the target
return True
elif matrix[r][c] < target: # Target to the right
c += 1 else: # Target must be above
r -= 1
return False # Target not found

Conclusion:
By leveraging the sorted properties of both rows and columns, we can reduce the search space efficiently. This approach runs in O(m + n) time, where m is the number of rows and n is the number of columns, making it highly efficient for large matrices.