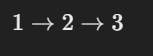Chapter 36: Graphs (Part 2)

In the last part of the DSA series, we explored the basic concepts of graphs, such as types of graphs, their representations, and traversals using DFS and BFS. In this chapter, we will dive deeper into the complexities of graphs, introducing more advanced topics. Graphs are a fundamental data structure used to model networks, relationships, and systems. Understanding the properties and algorithms that apply to graphs is essential for solving many real-world problems.

Here’s what we’ll cover in this chapter:

1. Connected Components

2. Second Cycle in Graphs

3. Cycle Detection in Undirected Graphs using DFS

4. Bipartite Graph

5. Cycle Detection in Directed Graphs using DFS

6. Topological Sorting using DFS

1. Connected Components

Connected Components in Graphs

In graph theory, a connected component refers to a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices in the supergraph. To understand this concept better, let's walk through it step by step with examples and visualizations.

i. Visualization of Different Types of Graphs

1. Graph Example:

   • Imagine a graph with nodes connected by edges, representing various relationships or pathways.

   • In this case, all nodes are connected either directly or indirectly through other nodes, forming a single connected component.

2. Binary Tree as a Graph:

   • Yes, a binary tree is a special kind of graph where each node has at most two children. It follows the rules of graphs, having nodes and edges (edges being parent-child connections).

3. Single Node as a Graph:

   • A single node with no edges is also considered a graph. It’s the simplest form of a graph—a single vertex with no connections.

Are these all a single graph?

• Not necessarily. These could be separate parts within a graph, not connected to each other. This is where the concept of Connected Components comes into play. A graph does not need to be fully connected. It can have multiple disconnected components, each of which is a subgraph on its own.

Concept of Connected Components

• When we discuss graph traversal algorithms like DFS (Depth-First Search) and BFS (Breadth-First Search), we generally start from a source node (src). We then traverse node-to-node from that source, covering all reachable nodes from that point.

• However, if a graph consists of multiple disconnected components (like in our visualization example), starting from a node in one component won't allow you to access nodes in other components. In such cases, a single traversal won't cover the entire graph.

Visual Explanation:

Imagine you have three separate parts of a graph:

• Part 1: Nodes connected as a small tree-like structure.

• Part 2: A single node standing alone.

• Part 3: Another binary tree structure disconnected from Part 1.

If you start traversing using DFS or BFS from a node in Part 1, you will only cover nodes within Part 1. The traversal cannot reach nodes in Part 2 or Part 3 because they are not connected.

How to Traverse Disjoint Components

To handle disjoint components, we modify the traversal method to ensure all nodes across different components are visited. Here's how we do it conceptually:

1. Loop Through All Nodes:

   • We iterate through every node in the graph using a loop. This loop will attempt to start the DFS traversal from every node in the graph.

2. Use a Boolean Array (vis[]):

   • We maintain a boolean array (vis[]) where each element indicates whether a node has been visited. Initially, all values are set to false.

3. Call a Helper Function:

   • We create a helper function, often called dfsUtil or dfsHelper, to perform the actual DFS traversal. This helper function is responsible for exploring all nodes reachable from a given start node.

   • Within the loop:

     • If a node (i) hasn’t been visited (!vis[i]), we call the helper function on this node. This marks all reachable nodes from i as visited.

Visualization of DFS Helper Function

When we create the DFS helper function (dfsUtil), we follow these steps:

1. Mark the Node as Visited:

   • When the function is called for a node, it marks that node as visited in the boolean array (vis[]).

2. Explore All Neighboring Nodes:

   • For the current node, the function explores all its neighbors (nodes directly connected by an edge).

   • For each neighbor:

     • If it has not been visited, the function is called recursively on that neighbor, marking and exploring further.

3. Recursive Exploration:

   • This recursive approach ensures that all nodes in a connected component are visited before the function terminates.

   • Once the DFS traversal for one component is complete, the main loop continues to the next node (i). If the node is part of a new component and hasn’t been visited, the helper function is called again, starting the DFS traversal for this new component.

The Flow of Traversal:

1. Iterate Over All Nodes (Main DFS Function):

   • The main function loops over each node.

   • For each unvisited node, it calls the helper function (dfsUtil).

2. DFS Helper Function:

   • When called, the helper function marks the node as visited.

   • It then recursively calls itself for all unvisited neighbors.

3. Traversal Completes for One Component:

   • Once all nodes in a component are visited, the helper function returns to the main loop.

   • The main loop continues to find the next unvisited node, ensuring that all components are covered.

Example Walkthrough

Let's say we have a graph with 6 nodes, divided into two connected components:

• Component 1: Nodes 0 - 1 - 2

• Component 2: Nodes 3 - 4 - 5

1. First Iteration:

   • Start at node 0. Call the DFS helper function, which marks nodes 0, 1, and 2 as visited.

   • Nodes 0, 1, and 2 form a connected component, and the traversal for this component is complete.

2. Next Iteration:

   • The main loop moves to node 1, but it’s already visited, so it skips to node 2, which is also visited.

   • The loop reaches node 3. Since it’s unvisited, it calls the DFS helper function again, marking nodes 3, 4, and 5 as visited.

3. By using this approach, we ensure that the entire graph, even with multiple disconnected parts, is traversed completely. Each disconnected segment forms its own connected component.

Why is This Important?

• Understanding and finding connected components is crucial in graph algorithms. It helps in applications like network analysis, social media connectivity, and clustering problems where isolated groups need to be identified and processed separately.

This method of using a loop and a helper function ensures that we can handle any graph structure, whether it's connected or composed of several disjoint components.

Practical Scenarios of Connected Components:

1. Social Networks:

   • Think of people as nodes, and friendships as edges. A connected component could represent a group of friends where each person knows another, but no one in this group knows anyone outside the group. Multiple groups of friends (connected components) exist, but they don’t overlap.

Let’s Dive into the Code

Here’s how the code works:

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class Connected {
    // Class to represent an Edge in the graph
    static class Edge {
        int src;
        int dest;
        int wt;

        public Edge(int s, int d, int w) {
            this.src = s;
            this.dest = d;
            this.wt = w;
        }
    }

    // Method to create the graph
    static void createGraph(ArrayList<Edge>[] graph) {
        for (int i = 0; i < graph.length; i++) {
            graph[i] = new ArrayList<>();
        }

        // Adding edges to represent connections between nodes
        graph[0].add(new Edge(0, 1, 1));
        graph[0].add(new Edge(0, 2, 1));
        graph[1].add(new Edge(1, 0, 1));
        graph[1].add(new Edge(1, 3, 1));
        graph[2].add(new Edge(2, 0, 1));
        graph[2].add(new Edge(2, 4, 1));
        graph[3].add(new Edge(3, 1, 1));
        graph[3].add(new Edge(3, 4, 1));
        graph[3].add(new Edge(3, 5, 1));
        graph[4].add(new Edge(4, 2, 1));
        graph[4].add(new Edge(4, 3, 1));
        graph[4].add(new Edge(4, 5, 1));
        graph[5].add(new Edge(5, 3, 1));
        graph[5].add(new Edge(5, 4, 1));
        graph[5].add(new Edge(5, 6, 1));
        graph[6].add(new Edge(6, 5, 1));
    }

    // The main BFS function that calls the helper function
    public static void bfs(ArrayList<Edge>[] graph) {
        boolean[] vis = new boolean[graph.length];
        int componentCount = 0;

        // Loop through all nodes to ensure we check every component
        for (int i = 0; i < graph.length; i++) {
            if (!vis[i]) {
                componentCount++;
                System.out.println("Connected Component " + componentCount + ":");
                bfsUtil(graph, vis, i);
                System.out.println(); // For separation between components
            }
        }
    }

    // BFS helper function that explores nodes layer by layer
    public static void bfsUtil(ArrayList<Edge>[] graph, boolean[] vis, int startNode) {
        Queue<Integer> q = new LinkedList<>();
        q.add(startNode); // Start traversal from this node

        while (!q.isEmpty()) {
            int curr = q.remove();
            if (!vis[curr]) {
                System.out.print(curr + " ");
                vis[curr] = true;

                // Add all neighboring nodes to the queue
                for (int i = 0; i < graph[curr].size(); i++) {
                    Edge e = graph[curr].get(i);
                    q.add(e.dest);
                }
            }
        }
    }

    // The main method to set up and run the code
    public static void main(String[] args) {
        /*
         * Graph visualization:
         *     1-----------3
         *    /            | \
         *   /             |  \
         *  0              |   5
         *   \             |  / \
         *    \            | /   \
         *      2----------4     6
         */
        int V = 7;
        ArrayList<Edge>[] graph = new ArrayList[V];
        createGraph(graph);
        bfs(graph);
    }
}

1. What Are Connected Components?

   • In a graph, a connected component is a set of vertices that are connected to each other, but not connected to any other vertices outside the set.

   • A graph may have multiple connected components. For example, imagine three groups of friends who only talk among themselves and not with other groups. Each group is a separate "connected component."

2. Examples of Connected Components:

   • Single Node: A single node with no edges is a connected component by itself.

   • Binary Tree: A binary tree is a graph where each node has connections (edges) to its left and right children. It is also a connected component.

   • Disjoint Components: A graph can have several separate parts (disjoint components). They are not connected to each other, which is where the concept of connected components comes into play.

Why Connected Components Matter

• In previous lessons, when we explored DFS (Depth-First Search) or BFS (Breadth-First Search), we assumed the entire graph was connected, meaning we could traverse from a single starting node (src) to all other nodes. But that only works if there is a path from the starting node to every other node.

• If the graph has disjoint components (separate clusters of nodes), you can't traverse the entire graph from just one starting point. We need to modify our approach to handle this situation.

How Do We Traverse a Graph with Disconnected Components?

1. Using BFS/DFS with a Helper Function:

   • We need to create two functions:

     • Main Function: This function will loop through every node and check if it's been visited. If it hasn’t, we’ll call our helper function.

     • Helper Function: This is a function (like BFS or DFS) that helps explore all nodes connected to the given node. It does the actual work of traversing the graph.

2. Why Two Functions?

   • The main function ensures we cover all parts of the graph, including disjoint components. The helper function explores each part completely before returning control to the main function to check the next unvisited node.

2. Cycle in Graphs

Let’s explore the concept of cycles in graphs, why it's important to detect them, and how they can appear in undirected and directed graphs. We will also discuss how to detect cycles using different methods.

2.1. Understanding Cycles in Graphs

A cycle in a graph occurs when you start from a node, traverse through a sequence of edges, and return to the starting node. Unlike in data structures like linked lists (where cycles ruin the structure), cycles in graphs are natural and often expected. However, for certain operations and algorithms, it's necessary to detect these cycles.

2.2. Cycle Detection in Undirected Graphs

An undirected graph is a graph where edges have no direction, meaning the connection between two vertices is bidirectional.

• Example:

       0---1
       |   |
       3---2
  

  • In this graph, you can see that there is a cycle involving vertices 0 -> 1 -> 2 -> 3 -> 0.

Why Detect Cycles?

• Cycles in undirected graphs might indicate an issue in network design or redundancy in communication systems. They are particularly relevant when verifying tree-like structures where cycles are not allowed.

Methods to Detect Cycles in Undirected Graphs

1. DFS (Depth-First Search):

   • DFS is efficient and useful for cycle detection. While traversing the graph, if you encounter a visited node that is not the immediate parent, it indicates a cycle.

2. BFS (Breadth-First Search):

   • BFS can also detect cycles. If a node is revisited and is not the parent of the current node in the traversal, then a cycle exists.

3. Disjoint Set Union (Union-Find):

   • This method is especially effective for cycle detection in dynamic graph construction. If two nodes are already in the same set and you try to connect them again, it indicates a cycle.

2.3. Cycle Detection in Directed Graphs

A directed graph (or digraph) has edges with direction, meaning each edge goes from one vertex to another and not both ways.

• Example:

        1 ---> 2 ---> 3
        ^             |
        |             v
        5 <--- 4 <----
  

  • Here, there is a cycle: 1 -> 2 -> 3 -> 4 -> 5 -> 1.

Why Detect Cycles in Directed Graphs?

• Cycles in directed graphs can affect processes like task scheduling (e.g., using topological sorting). A cycle indicates a dependency loop, which prevents proper task execution.

Methods to Detect Cycles in Directed Graphs

1. DFS (Depth-First Search):

   • While performing DFS, you keep track of nodes in the current traversal path (using a recursion stack). If you encounter a node that is already in the current path, it indicates a cycle.

   • Why DFS? DFS is generally more efficient for cycle detection in directed graphs as it directly explores paths and backtracks when necessary.

2. BFS (Kahn’s Algorithm):

   • This algorithm uses topological sorting and checks if all nodes can be processed without forming a cycle. If not, a cycle exists.

3. Topological Sort:

   • If a directed graph can be topologically sorted without any issues, it means no cycles are present. If not, cycles exist.

2.4. How Cycles Exist in Undirected and Directed Graphs

Undirected Graph Example:

• Consider the graph:

        1 --- 2
        |     |
        4 --- 3
  

  • This graph has a cycle involving nodes 1 -> 2 -> 3 -> 4 -> 1.

  • When using DFS, if you start from node 1 and traverse to 2, then 3, and then 4, when you try to revisit 1 (which is not the parent of 4), a cycle is detected.

Directed Graph Example:

• Consider the graph:

        1 ---> 2 ---> 3
        ^             |
        |             v
        5 <--- 4 <----
  

  • Here, you have a cycle: 1 -> 2 -> 3 -> 4 -> 5 -> 1.

  • Using DFS:

    • If you start from node 1, traverse to 2, then 3, 4, and 5, when you try to go back to 1, you’ll detect a cycle because 1 is already in the recursion stack.

2.5. Why We Use DFS for Cycle Detection

• Efficiency: DFS allows you to explore all paths from a node and backtrack efficiently. This makes it ideal for cycle detection, especially in directed graphs.

• Path Tracking: In directed graphs, DFS can track nodes currently in the path (using a recursion stack), which helps identify cycles efficiently.

2.6. Visualizing the Examples

Let’s visualize these examples:

Undirected Graph Visualization:

    0---1
    |   |
    3---2

• This graph has one cycle (0 -> 1 -> 2 -> 3 -> 0).

Directed Graph Visualization:

    1 ---> 2 ---> 3
    ^             |
    |             v
    5 <--- 4 <----

• This graph has a cycle (1 -> 2 -> 3 -> 4 -> 5 -> 1).

Conclusion

• Cycles are common in both directed and undirected graphs, but they serve different purposes and implications depending on the context.

• Detecting cycles helps in optimizing graph structures, avoiding deadlock situations, and ensuring efficient execution in systems like scheduling and networking.

3. Cycle Detection in Undirected Graphs using DFS

Cycle detection in an undirected graph is important for understanding if the graph contains loops. We can detect a cycle using DFS by backtracking when we encounter a previously visited vertex that is not the direct parent of the current vertex.

• Approach:

  • During DFS traversal, if we visit a vertex that is already visited and is not the parent of the current node, a cycle exists.

• Code Example (DFS for Cycle Detection in Undirected Graph):

public class Graph {
    private LinkedList<Integer> adj[];

    public Graph(int v) {
        adj = new LinkedList[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkedList<>();
        }
    }

    public void addEdge(int v, int w) {
        adj[v].add(w);
        adj[w].add(v);
    }

    public boolean isCyclicUtil(int v, boolean visited[], int parent) {
        visited[v] = true;

        for (Integer i : adj[v]) {
            if (!visited[i]) {
                if (isCyclicUtil(i, visited, v)) return true;
            } else if (i != parent) {
                return true;
            }
        }
        return false;
    }

    public boolean isCyclic() {
        boolean[] visited = new boolean[adj.length];

        for (int u = 0; u < adj.length; u++) {
            if (!visited[u]) {
                if (isCyclicUtil(u, visited, -1)) return true;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        Graph g = new Graph(5);
        g.addEdge(0, 1);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(1, 3);
        g.addEdge(3, 4);

        if (g.isCyclic()) {
            System.out.println("Graph contains cycle");
        } else {
            System.out.println("Graph doesn't contain cycle");
        }
    }
}

4. Bipartite Graph

A bipartite graph is a graph whose vertices can be divided into two disjoint sets such that no two graph vertices within the same set are adjacent. A graph is bipartite if and only if it contains no odd-length cycles.

• Check for Bipartite Graph using DFS:

  • You can use a coloring technique, assigning two different colors to the two sets. If a vertex has the same color as its adjacent vertex during DFS, the graph is not bipartite.

5. Cycle Detection in Directed Graphs using DFS

Cycle detection in directed graphs requires a different approach because cycles can occur in more subtle ways. Using DFS, we can detect cycles by marking the vertices during traversal.

• Approach:

  • Use a recursion stack to keep track of the vertices being visited. If a vertex is revisited while it's still in the recursion stack, a cycle is detected.

6. Topological Sorting using DFS

Topological Sorting: Theory and Visualization

Topological sorting is a fundamental concept in graph theory used to organize the vertices of a directed acyclic graph (DAG) in a linear order. This order ensures that for every directed edge ( u \rightarrow v ), vertex ( u ) appears before vertex ( v ) in the sorted list.

Definition

Topological Sorting: It is a linear ordering of the vertices in a directed graph such that for every directed edge ( u—> v ), vertex ( u ) comes before vertex ( v ) in the ordering.

Key Points:

• Directed Acyclic Graph (DAG): Topological sorting is applicable only to DAGs. A DAG is a directed graph that contains no cycles, meaning there is no way to start at a vertex ( v ) and follow a sequence of edges that eventually loops back to ( v ).

• Existence of Multiple Orders: A DAG can have multiple valid topological sorts. For example, the graph may allow for different valid sequences of the vertices based on the dependencies defined by the edges.

Visualization of Topological Sorting

Let's consider a simple example:

Graph Structure:

  1
 / \
2   3
 \ /
  4

Topological Sorting Example:

1. From the above graph, we can create a topological sort. The valid topological orders could be:

   • Order 1: ( 1, 2, 3, 4 )

   • Order 2: ( 1, 3, 2, 4 )

Both orders respect the directed edges, ensuring that all dependencies are satisfied.

Practical Applications

Topological sorting is often used in scenarios involving dependencies, where certain tasks must be completed before others. Here’s a practical example using cooking actions:

1. Actions:

   • Action 1: Boil water

   • Action 2: Add masala

   • Action 3: Add Maggi

   • Action 4: Serve Maggi

Dependency Graph:

• Action 1 must be done before Action 2 and Action 3.

• Action 2 and Action 3 must be done before Action 4.

Graph Representation:

  1
 / \
2   3
 \ /
  4

Topological Orders:

• Possible valid orders:

  

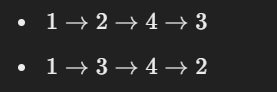
In this cooking example, the dependencies are crucial, as you cannot add masala or Maggi before boiling water.

Example in Software Development

In software development, tasks often depend on one another, making topological sorting valuable for scheduling tasks:

1. Install OS

2. Install Visual Studio Code (VS Code)

3. Install Extensions

Dependency Graph:

1 → 2 → 3

Topological Order:

• The only valid order would be:

  • 

Here, the installation of the operating system must occur before installing any applications or extensions.

How Topological Sorting is Done

Topological sorting can be accomplished using Depth-First Search (DFS):

1. DFS Approach:

   • Initialize a stack to keep track of the order of vertices.

   • Maintain a visited array to track which vertices have been processed.

   • Perform a standard DFS traversal:

     • Mark the current vertex as visited.

     • Recur for all adjacent vertices that have not been visited.

     • Push the current vertex onto the stack once all its neighbors have been processed.

2. Result:

   • Once the DFS completes, the stack will contain the vertices in topologically sorted order. Pop the vertices from the stack to retrieve the final order.

import java.util.ArrayList;
import java.util.Stack;

public class TopologicalSorting {

    // Class representing an edge in the graph
    static class Edge {
        int src; // Source vertex
        int dest; // Destination vertex

        public Edge(int s, int d) {
            this.src = s;
            this.dest = d;
        }
    }

    // Method to create a graph represented as an adjacency list
    static void createGraph(ArrayList<Edge> graph[]) {
        // Initialize each list in the graph
        for (int i = 0; i < graph.length; i++) {
            graph[i] = new ArrayList<>(); 
        }

        // Add edges to the graph
        graph[2].add(new Edge(2, 3)); // Edge from 2 to 3
        graph[3].add(new Edge(3, 1)); // Edge from 3 to 1
        graph[4].add(new Edge(4, 0)); // Edge from 4 to 0
        graph[4].add(new Edge(4, 1)); // Edge from 4 to 1
        graph[5].add(new Edge(5, 0)); // Edge from 5 to 0
        graph[5].add(new Edge(5, 2)); // Edge from 5 to 2
    }

    // Method to perform topological sorting on the graph
    public static void topSort(ArrayList<Edge>[] graph) {
        boolean vis[] = new boolean[graph.length]; // Visited array to track visited vertices
        Stack<Integer> s = new Stack<>(); // Stack to store the topological order

        // Perform DFS for each unvisited vertex
        for (int i = 0; i < graph.length; i++) {
            if (!vis[i]) {
                topSortUtil(graph, i, vis, s); // Call DFS helper function
            }
        }

        // Print the topological order
        while (!s.isEmpty()) {
            System.out.print(s.pop() + " ");
        }
    }

    // Helper method to perform DFS and push vertices onto the stack
    public static void topSortUtil(ArrayList<Edge>[] graph, int curr, boolean vis[], Stack<Integer> s) {
        vis[curr] = true; // Mark the current vertex as visited

        // Visit all the adjacent vertices
        for (int i = 0; i < graph[curr].size(); i++) {
            Edge e = graph[curr].get(i);
            if (!vis[e.dest]) {
                topSortUtil(graph, e.dest, vis, s); // Recursive call for unvisited vertex
            }
        }
        s.push(curr); // Push the current vertex to the stack after visiting all adjacent vertices
    }

    // Main method to execute the topological sorting
    public static void main(String[] args) {
        int v = 6; // Number of vertices
        ArrayList<Edge> graph[] = new ArrayList[v]; // Create the graph
        createGraph(graph); // Initialize the graph with edges
        topSort(graph); // Perform topological sorting
    }
}

The code implements topological sorting using Depth First Search (DFS) for a directed acyclic graph (DAG). It consists of the following key components:

1. Graph Representation: The graph is represented using an adjacency list, where each vertex has a list of edges representing outgoing connections.

2. Topological Sorting: The algorithm uses DFS to determine the order in which vertices should be processed.

3. Stack: A stack is utilized to store the vertices in topologically sorted order.

Code Breakdown

1. Graph Representation

static class Edge {
    int src; // Source vertex
    int dest; // Destination vertex

    public Edge(int s, int d) {
        this.src = s;
        this.dest = d;
    }
}

• This class represents an edge in the graph. Each edge has a source (src) and a destination (dest).

2. Creating the Graph

static void createGraph(ArrayList<Edge> graph[]) {
    // Initialize each list in the graph
    for (int i = 0; i < graph.length; i++) {
        graph[i] = new ArrayList<>(); 
    }

    // Add edges to the graph
    graph[2].add(new Edge(2, 3)); // Edge from 2 to 3
    graph[3].add(new Edge(3, 1)); // Edge from 3 to 1
    graph[4].add(new Edge(4, 0)); // Edge from 4 to 0
    graph[4].add(new Edge(4, 1)); // Edge from 4 to 1
    graph[5].add(new Edge(5, 0)); // Edge from 5 to 0
    graph[5].add(new Edge(5, 2)); // Edge from 5 to 2
}

• This method initializes the graph as an adjacency list and adds edges to represent the relationships between the vertices.

Graph Visualization:

The graph after creating the edges looks like this:

   2
   |
   v
   3 → 1
   |
   ↑
   4 → 0
   |
   |
   5
   |
   ↓
   0

• Edges:

  • 2 → 3

  • 3 → 1

  • 4 → 0

  • 4 → 1

  • 5 → 0

  • 5 → 2

3. Topological Sorting

public static void topSort(ArrayList<Edge>[] graph) {
    boolean vis[] = new boolean[graph.length]; // Visited array to track visited vertices
    Stack<Integer> s = new Stack<>(); // Stack to store the topological order

    // Perform DFS for each unvisited vertex
    for (int i = 0; i < graph.length; i++) {
        if (!vis[i]) {
            topSortUtil(graph, i, vis, s); // Call DFS helper function
        }
    }

    // Print the topological order
    while (!s.isEmpty()) {
        System.out.print(s.pop() + " ");
    }
}

• Visited Array: This array keeps track of which vertices have been visited during the DFS.

• Stack: This stack stores the vertices in the topological order.

• The method iterates through each vertex; if it has not been visited, it calls the helper function topSortUtil.

4. DFS Helper Function

public static void topSortUtil(ArrayList<Edge>[] graph, int curr, boolean vis[], Stack<Integer> s) {
    vis[curr] = true; // Mark the current vertex as visited

    // Visit all the adjacent vertices
    for (int i = 0; i < graph[curr].size(); i++) {
        Edge e = graph[curr].get(i);
        if (!vis[e.dest]) {
            topSortUtil(graph, e.dest, vis, s); // Recursive call for unvisited vertex
        }
    }
    s.push(curr); // Push the current vertex to the stack after visiting all adjacent vertices
}

• This function performs DFS on the graph:

  • Marks the current vertex as visited.

  • Iterates through all adjacent vertices, calling itself recursively for unvisited vertices.

  • After visiting all adjacent vertices, it pushes the current vertex onto the stack.

5. Main Method

public static void main(String[] args) {
    int v = 6; // Number of vertices
    ArrayList<Edge> graph[] = new ArrayList[v]; // Create the graph
    createGraph(graph); // Initialize the graph with edges
    topSort(graph); // Perform topological sorting
}

• This method sets up the graph and invokes the topological sorting function.

Output Visualization

When you run the code, the output is:

5 4 2 3 1 0

This means that in a valid topological order, the vertices are sorted such that all dependencies are respected.

Interpretation of the Output:

• 5 comes before 0 and 2, meaning task 5 should be completed before tasks 0 and 2.

• 4 comes before 0 and 1.

• 2 comes before 3, and 3 comes before 1.

Conclusion

The topological sorting algorithm effectively organizes the vertices of a directed acyclic graph (DAG) according to their dependencies, allowing for a clear order of operations. This code demonstrates how to implement the sorting using DFS while maintaining an intuitive and clear structure for representing edges and processing the graph.

Conclusion

In this chapter, we covered several advanced topics related to graphs, including detecting cycles, connected components, and understanding bipartite graphs. These concepts are critical for solving complex problems in competitive programming and real-world applications. Keep practicing these techniques to gain a deeper understanding!