Beyond Gradient Descent: Theoretical Analysis

---

Audience: ML Engineers, NLP Practitioners, AI Researchers

Keywords: NLP, Transformers, Gradient Descent, Optimisation, Euclidean Geometry, Non-Euclidean Geometry, Hyperbolic Geometry, Elliptic Geometry, High-Dimensional Data, Discrete Data, Symbolic Reasoning, LLMs, Reasoning, Hierarchical Data, Global Context, Optimisation Landscapes.

Technical background

This post targets ML engineers and NLP practitioners familiar with transformer architectures, gradient descent optimisation, and the challenges of high-dimensional data. It delves into the limitations of applying Euclidean geometry-based optimization to the inherently discrete nature of language data. Key concepts explored include non-Euclidean geometries (hyperbolic and elliptic), their application to NLP tasks, and the potential for integrating these geometries with existing NLP paradigms. Readers should be comfortable with basic geometric concepts and the principles of gradient descent. Familiarity with the limitations of current LLMs and the concept of symbolic reasoning will further enhance understanding, though not strictly required.

---

Introduction

The transformer architecture has revolutionized Natural Language Processing (NLP), achieving remarkable feats in language understanding and generation. However, a critical examination reveals a fundamental mismatch: the continuous nature of gradient descent optimization, the workhorse of deep learning, clashes with the inherently discrete nature of language data. While techniques like dimensionality reduction offer some relief, they don't address the core issue. This post argues for exploring non-Euclidean topologies, specifically hyperbolic and elliptic geometries, as a more natural and efficient framework for NLP optimization.

The Discrepancy: Gradient Descent and Discrete Data

Gradient descent thrives in continuous, smooth Euclidean spaces, like those encountered in image processing. Language, however, is discrete. Words are symbolic units, and small changes in their vector representations can lead to significant semantic shifts. While word embeddings map discrete words into continuous vectors, this is an approximation, not a perfect solution. Gradient updates in these high-dimensional embedding spaces can cause unpredictable semantic jumps, hindering effective optimisation.

Dimensionality Reduction: A Temporary Fix

Dimensionality reduction techniques, guided by principles like the Johnson-Lindenstrauss Lemma, offer some respite by projecting high-dimensional data into lower dimensions while preserving pairwise distances. This simplifies the optimisation landscape, making gradient descent more tractable. However, it merely smooths the process without addressing the fundamental disconnect between discrete language and continuous optimization.

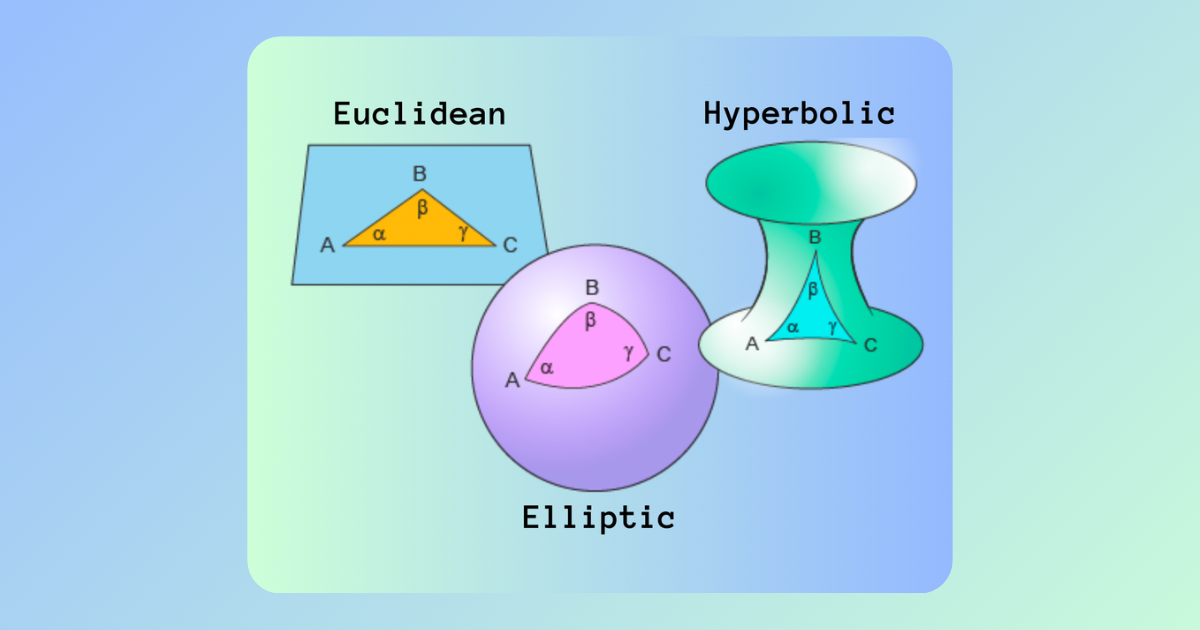
Beyond Euclidean Space: Embracing Hyperbolic and Elliptic Geometries

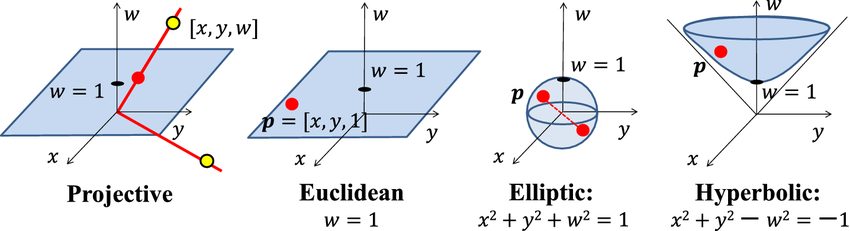
To truly bridge this gap, we must look beyond Euclidean space. Non-Euclidean geometries, specifically hyperbolic and elliptic geometries, offer a more natural framework for representing the inherent structure of language:

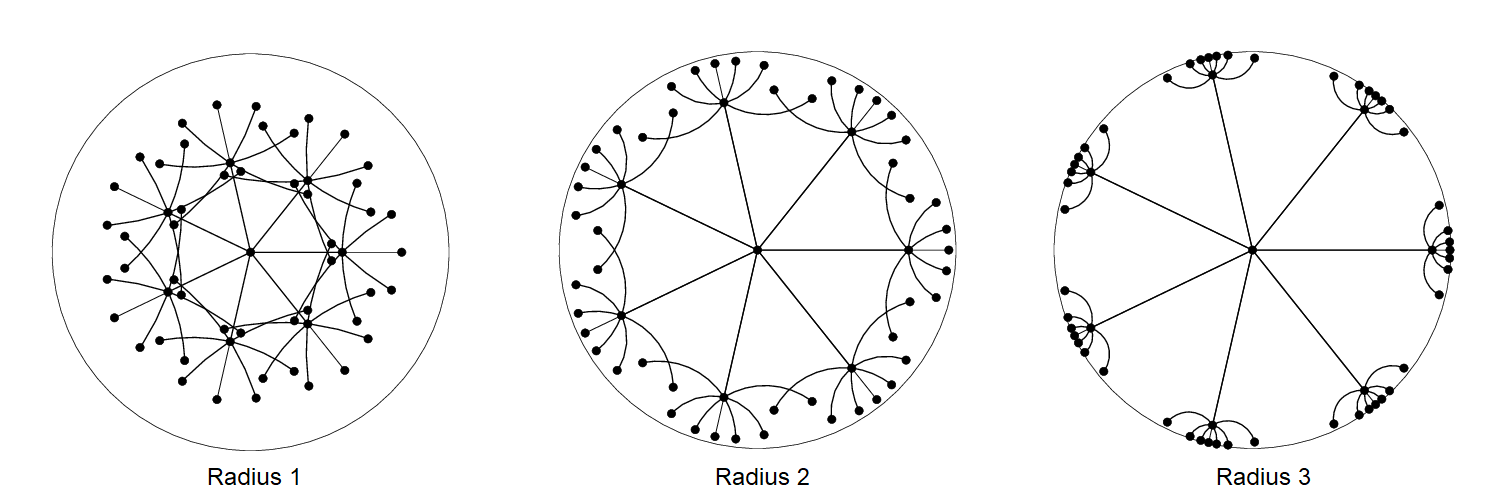
1. Hyperbolic Geometry: Capturing Hierarchical Relationships

Hyperbolic space, characterised by exponential distance growth from a central point, excels at modelling hierarchical structures prevalent in language, such as syntactic trees and semantic relationships.

• Benefits:

  • Natural Hierarchy Representation: Captures hierarchical relationships between words and phrases more effectively than Euclidean space.

  • Compact Representation: Represents large hierarchies efficiently with fewer dimensions, reducing computational overhead.

  • Improved Gradient Flow: Facilitates more stable gradient updates, mitigating issues like vanishing or exploding gradients.

2. Elliptic Geometry: Smoothing Global Relationships

Elliptic geometry, where all lines eventually intersect, complements hyperbolic geometry by capturing global relationships and smoothing contextual information across a text.

• Benefits:

  • Global Structure Capture: Models global relationships between words and concepts, important for tasks like summarization and translation.

  • Dimensionality Reduction with Global Coherence: Reduces dimensionality while preserving global information, unlike Euclidean approaches.

  • Improved Convergence: Facilitates faster convergence of gradient descent due to the compact nature of elliptic spaces.

Addressing NLP's Core Challenges

These non-Euclidean geometries directly address the core challenges of applying gradient descent to NLP:

• Handling Discreteness: Provide a better fit for discrete language data, mitigating the mismatch with continuous optimization.

• Overcoming Dimensionality: Reduce dimensionality while preserving crucial structural information, simplifying the optimization landscape.

• Improved Optimization Landscapes: Offer more structured and well-behaved optimization landscapes, leading to more efficient and stable gradient updates.

Integrating with Existing Paradigms and Future Directions

While exploring non-Euclidean geometries is crucial, it doesn't necessitate abandoning transformers entirely. Instead, we can envision hybrid models that combine the strengths of transformers with the structural advantages of non-Euclidean spaces. Furthermore, integrating symbolic reasoning systems or leveraging graph-based models can further enhance the ability of NLP systems to handle the complex, discrete, and hierarchical nature of language.

Exploring alternative optimisation techniques beyond gradient descent, such as natural gradient descent or discrete optimisation methods, is another promising avenue. Current LLMs primarily rely on statistical pattern matching and struggle with true reasoning. Moving beyond these limitations requires a multifaceted approach, including exploring new geometries, integrating different AI paradigms, and developing more sophisticated optimisation techniques.

Conclusion: A Path Towards True Language Understanding

The current dominance of gradient descent in Euclidean space for NLP, while impressive, represents a bottleneck. Embracing non-Euclidean geometries offers a path towards more natural, efficient, and ultimately more powerful NLP models. This shift, combined with exploring alternative AI paradigms and optimisation techniques, can unlock the next generation of NLP systems capable of true reasoning and deeper language understanding.